Quick Look
Grade Level: 6 (5-7)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00 This activity uses non-expendable (reusable) LEGO® MINDSTORMS® robot kits; see the Materials List for details.
Group Size: 5
Activity Dependency: None
Subject Areas: Measurement

Summary
Students learn about the concepts of accuracy and approximation as they pertain to robotics, gain insight into experimental accuracy, and learn how and when to estimate values that they measure. Students also explore sources of error stemming from the robot setup and rounding numbers.Engineering Connection
For engineers, proper comparison of data is important for accurate measurements and troubleshooting of robotic machines for quality assessment. Interpretation of data also gives important insight into the accuracy of an experimental setup, as well as approximations that may take place, which can negatively affect experimental data.
Learning Objectives
After this activity, students should be able to:
- Work with decimals in measurement estimations.
- Compare data values and find percent error.
- Make connections between circumference and linear measurement.
- Identify possible physical sources of error in an experimental set-up.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Use place value understanding to round whole numbers to the nearest 10 or 100.
(Grade
3)
More Details
Do you agree with this alignment?
-
Use place value understanding to round decimals to any place.
(Grade
5)
More Details
Do you agree with this alignment?
-
Convert like measurement units within a given measurement system.
(Grade
5)
More Details
Do you agree with this alignment?
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent.
(Grade
6)
More Details
Do you agree with this alignment?
-
Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.
(Grade
6)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Asking questions and making observations helps a person to figure out how things work.
(Grades
K -
2)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
Round numbers less than 1,000 to the nearest tens and hundreds
(Grade
4)
More Details
Do you agree with this alignment?
-
Convert like measurement units within a given measurement system.
(Grade
5)
More Details
Do you agree with this alignment?
-
Use place value understanding to round decimals to any place.
(Grade
5)
More Details
Do you agree with this alignment?
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Find a percent of a quantity as a rate per 100 (e.g., 30% of a quantity means 30/100 times the quantity); solve problems involving finding the whole, given a part and the percent.
(Grade
6)
More Details
Do you agree with this alignment?
-
Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.
(Grade
6)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- LEGO MINDSTORMS EV3 robot, such as EV3 Core Set (5003400) at https://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3
- LEGO MINDSTORMS Education EV3 Software 1.2.1, free online, you have to register a LEGO account first; at https://www.lego.com/en-us/mindstorms/downloads/download-software
- computer, loaded with EV3 1.2.1 software
- marker
- meter stick
- caliper, to make circumference measurements (recommended, but if not available, use a ruler to measure the diameter of each wheel or use a string and wrap it around the wheel to measure the circumference)
- piece of paper (8.5 x 11 inch)
- rubber band
- Accuracy Pre-Evaluation, Accuracy Worksheet, Accuracy Post-Evaluation, one each per student
Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:
- LEGO MINDSTORMS NXT robot, such as the NXT Base Set
- computer, loaded with NXT 2.1 software
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_accuracy_activity1] to print or download.Pre-Req Knowledge
Familiarity with decimals, how to use a ruler, rounding basics, and units.
Introduction/Motivation
No robot or machine made by human beings works perfectly. Some machines are able to write books, cut materials and mass-produce millions of products that we use every day. This is an improvement in production compared to what each of us as humans could do alone. However, engineers and designers of these machines must manage error in their machine designs and functions. What do we mean by error?
Here's an example: a machine that cuts wooden beams is designed to cut them to a certain thickness, such as 50 mm. However, this machine (and most likely all other machines in existence today) may not cut the beams to exactly 50 mm. Some beams may be 51 mm thick, and others 49 mm thick. This means that the machinery may be able to cut the wood close to 50 mm, give or take 1 mm. We might claim that the machine cut the wood to a thickness of approximately 50 mm, because 49 mm is very close to 50 mm, but we could not claim that the thickness is exactly 50 mm. The differences from 50 mm may be due to how the machine cuts the wood, vibration of the machinery in motion, the type of saw used, or some other reason. That's why it is important to think about anything that could cause machine inaccuracies, and then measure how much the accuracy can vary, in terms of error. We can calculate error in terms of percent error between two values. We do this by first taking the difference between, for example, the 50 mm thickness of wood that you want, and the thickness of wood that actually came out of the machine, say 49 mm:
Measurement error: desired measurement – actual Measurement = 50 mm – 49 mm = 1 mm
Divide the measurement error just calculated by the desired measurement (50 mm) and multiply by 100 to get the percent error: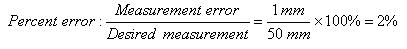

The percent error of the machine turns out to be 2%. We can also write a measured value along with its numerical error (the amount the cut could differ from 50 mm) as follows: 50±1 mm. This simply means that the measured value is expected to be 50 mm, plus or minus 1 mm of difference, which is the error. Thus, any measurement that falls in between 51 and 49, or within 2% of the desired value, is reasonable because it would be approximately equal to 50 mm.
Let's say you used a tool that allows you to measure the thickness of these beams to the nearest ten thousandth millimeter (this cannot be done with a regular ruler). When you measure a beam, it might give you a number: 50.7658. From looking at this number, you may just want to know if it clearly falls within the expected error of 50±1 mm. That means that if the measured value falls between the two values 51 and 49, then it is a value that is expected due to the machine error. If it does not, then the machine error may not be the only thing to be blamed for getting thicker or thinner beams than expected.
Therefore, you should round up to the nearest tenth. Given that the number in the hundredths place is a 6, we typically round the value up to 50.8. Now it is easy to see that 50.8 fits between 51 and 49, and that is why we can tell that the value 50.8 is a reasonable value, since it fits within the expected range of error. Knowing this means it should be taken into account when using it to build buildings or structures. If you wanted to use these beams to build a door frame, you would make sure that you leave enough space between the door and the frame so that the door won't be too big or too small to use.
Accuracy is very important to many machines that travel on land, in the sea and in the air. The accuracy of the machinery inside an automobile, ship or airplane determines if people can get to and from places without ending up in the wrong area of the map or without getting into accidents along the way. For example, if you are on a boat and set your course for an island, you would want the machinery involved to be accurate enough to get you to the island. The more accurate the machinery, the less error there will be in your actual course of travel. If the error is too great, the boat will miss the island. The distance involved and the path traveled shouldn't matter, since that is taken into account when machines are designed.
As consumers, engineers, designers or company workers, we can choose to accept or reject a given amount of error, depending on what our job demands. Today, we will see how accurate the LEGO MINDSTORMS EV3 robot is when performing a simple task: drawing a line.
Procedure
Before the Activity
- Gather materials and make copies of the handouts.
- Build basic EV3 robots, one per group, as outlined in the LEGO kit instruction manual. Set aside 30 minutes of building time, read instruction manual carefully and ensure all required pieces are present.
- Place one robot, one sheet of 8.5 x 11-inch paper and a marker at each group station.
- Modify the robot slightly to accommodate placement of the marker, as shown in Figure 1.
- Install the LEGO EV3 software (included in the LEGO EV3 kit) on a PC and run the LEGO EV3 programming part of the software. Write the program for the robot to move forward (shown in Figure 2). The program can easily be written in many ways; the Figure 2 program instructions are one example.

Figure 1. Attaching a marker to a LEGO robot. 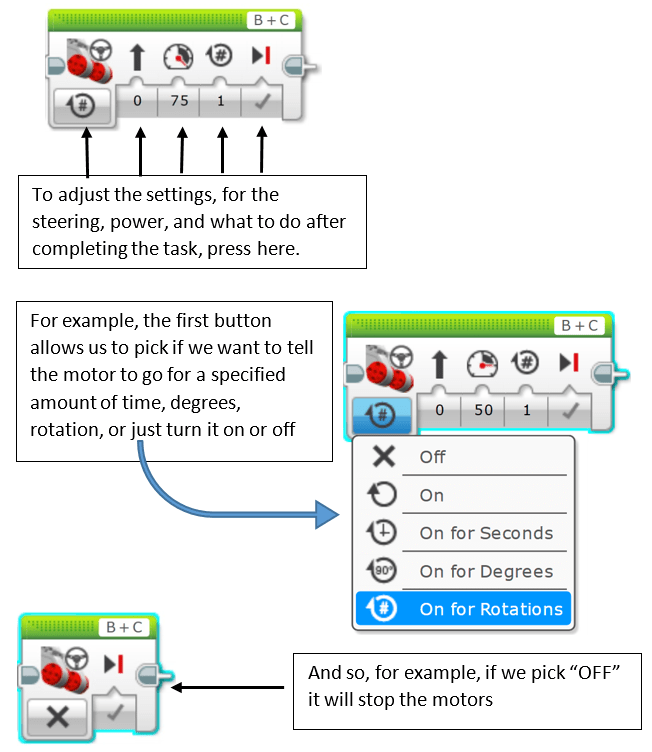
Figure 2. LEGO EV3 programming to move a robot forward.
With the Students
- Administer the Accuracy Pre-Evaluation.
- Provide students with the definition of accuracy and explain why it is important. (Give them a few real-world examples: The wheels on cars must be fitted so that they travel dependably in straight lines without veering to one side unintentionally and causing accidents. The path that a rocket takes to travel into space must be accurate, or else it may miss its destination—or even crash into it.)
- Divide the class into groups of five students each. Have each team assemble at a robot station.
- Working as teams, have students calculate the distance that their robots move forward after one rotation of the wheels. Then have robots travel one rotation forward, marking on the paper.
- Direct students to measure the lines drawn by their robots, either by ruler or caliper. Have them compare calculated values to measured values.
- Using the percent error equation introduced in the Introduction/Motivation section, help students calculate the percent errors of their trial runs.
- Repeat steps 7-9 again for two rotations. Explain that the longer the distance a robot travels, the more it may veer from its straight path. Error may build up due to wheel slip, robot shaking during operation, and general build quality of the robot. Therefore, it is important to see how the robot performs in the long run in order to see how much the robot can possibly veer off of its intended course, and take that into account when designing and programming the robot.
- Have students fill out the Accuracy Worksheet to keep their data organized for comparison purposes. Direct students to round their values to the nearest tenth.
- Have groups compare data and discuss what is seen in terms of consistency.
- Have students complete the Accuracy Post-Evaluation to assess how much they learned throughout the activity.
Vocabulary/Definitions
accuracy: How close a measured value is to the desired value.
approximation: An estimate or rough calculation; a measured value that is very close to the desired value.
error: The difference between a measured value and a desired value.
Assessment
Pre-Activity Assessment
Pre-Evaluation: Administer the six-question Accuracy Pre-Evaluation to gauge students' familiarity with the topics.
Activity Embedded Assessment
Worksheet: Have students complete the Accuracy Worksheet as they conduct the activity. Evaluate students on two criteria: conducting experimental measurements and interpreting the resulting data with respect to applied circumference theory. When conducting experimental measurements, expect groups to obtain similar error difference results given that the same robot was built for each group. For data interpretation, expect students to be able to recognize what can physically affect the trial run measured results, as well as gain insight as to how accurate a programmed EV3 robot can be in conducting a simple operation.
Post-Activity Assessment
Post-Evaluation: At activity end, administer the Accuracy Post-Evaluation. Review students' answers to gauge their understanding of the topics covered.
Safety Issues
- Carefully wrap the rubber band around the marker when attaching it to the robot.
Troubleshooting Tips
For additional references and troubleshooting tips on LEGO MINDSTORMS EV3 robot kits, go to http://ev3lessons.com/. Several examples, manuals and help menus are available to facilitate additional EV3 practice.
Physical conditions may impact the robot's ability to draw the line as desired, such as wheel alignment, robot weight, friction between the tires and the surface on which the robot runs, and so on. Check these items before the robot is used, so as to provide the best possible robot results.
Make sure that the marker is touching the paper by loosening the grey three-hole piece attached to the front of the robot.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!Copyright
© 2013 by Regents of the University of Colorado; original © 2011 Polytechnic Institute of New York UniversityContributors
Ronald PovedaSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: October 16, 2020


User Comments & Tips