Hands-on Activity Let's Take a Slice of Pi

Learning Objectives

After this activity, students should be able to:

• Build and program a basic LEGO MINDSTORMS EV3 robot.
• Measure the diameter and circumference of a circle.
• Calculate and understand the concept and value of pi.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

Each group needs:

• LEGO MINDSTORMS EV3 robot, such as EV3 Core Set (5003400) at https://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3
• LEGO MINDSTORMS Education EV3 Software 1.2.1, free online, you have to register a LEGO account first; at https://www.lego.com/en-us/mindstorms/downloads/download-software
• computer, loaded with EV3 1.2.1 software
• 1 marker or highlighter
• 1 large piece of white paper (create by taping together enough pieces of 8.5" x 11" [21.59cm x 27.94cm] white copier paper to cover the area the LEGO robot will travel; test the activity without the marker to determine the approximate robot travel area)
• 1 ruler (with centimeter markings)
• yarn
• 1 calculator
• tape
• notepad and pen

Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:

• LEGO MINDSTORMS NXT robot, such as the NXT Base Set
• computer, loaded with NXT 2.1 software

Worksheets and Attachments

Pre-Req Knowledge

Familiarity with making measurements using a ruler, division and multiplication, and the use of LEGO MINDSTORMS software.

Introduction/Motivation

It has been said that the universe would not be able to function without the remarkable concept of pi. However, the exact value of pi could not be properly expressed in the number system that we use; that is pi is an irrational number that cannot be expressed as a fraction and therefore it has an endless amount of decimal representations. Nonetheless, mathematicians have been able to estimate the value of pi to be 3.14... (Who can recite the first five decimal places of pi?) Knowing this value of pi, we can calculate the circumference of a circle given the diameter or radius.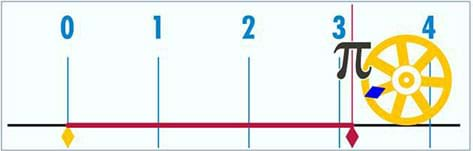

The importance of pi was recognized throughout history, and some historians suggest that it was discovered about 4,000 years ago. Around 2000 BC, both the Babylonians and the Egyptians had discovered the concept of pi and incorporated it in their architecture. However, at that time, both civilizations did not have a clear idea of what the exact value of pi was, but nonetheless, they had rough estimated values. It was not until almost 2,000 years later that Greek mathematicians (namely Archimedes) were able to improve upon the approximated value that the Babylonians and Egyptians used. Amazingly, today we are able to approximate pi to more than 6 billion digits. Now does anyone want to calculate 6 billion decimal digits of pi? Surely no one does; therefore this effort was made possible with the help of an advance powerful computing tool–the computer.

Procedure

Before the Activity

• Gather materials and make copies of the Pi Pre-Activity Worksheet, one per student.
• Make sure all the LEGO kits are complete with the parts correctly divided.
• Prepare the floor working area with a large piece of white paper and use tape to secure it to the floor.
• Divide the class into groups of four students each. (optional: Assign roles to each team member, or else let the students decide.)

With the Students

1. Discuss and review the definitions of diameter, radius and circumference.
2. Write on the classroom board the relationship of pi with circumference and diameter in sentence form: pi = circumference ÷ diameter.
3. Directly under the sentence relationship, write the relationship in a mathematical format:

   

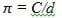
where C is the circumference and d is the diameter.

4. Emphasize the ratio relationships written. Rearrange relationship to show that:

   

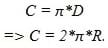
5. Pass out the materials to each group.
6. Have students complete a brief pre-activity experiment:

• Refer to the worksheet.
• Once students are finished with the worksheet, go over the assessment part of the activity as a class to ensure that students understand the concept of pi, circumference and diameter.

7. After the discussion of the pre-activity experiment, have groups start the activity.

• Open up the LEGO EV3 kit and find the instruction manual to build the standard robot chassis titled "LEGO MINDSTORMS Education."
• In the lower level of the kit, look for the battery package of the EV3 brain. Put them together according to page 3's (right side of the page) instruction.
• Go to page 4 of the manual and follow the building instructions (Step 1) up to page 38 (Step 40).
• To attach a marker to the chassis, follow the steps in Figure 1.

  

• Once the robot is built, load the MINDSTORMS software on the computer.
• Create a new program file and name it "dragTurn." This makes the robot do a drag turn so that it draws a circle on the paper using the marker. See Figure 2 for programming instructions.

  

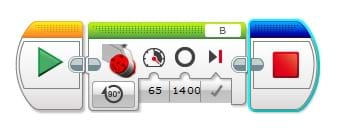
• Download "dragTurn" onto EV3 and make sure that the marker is touching the large, taped-down piece of paper on the floor.
• Run the program and watch the robot do a drag turn, drawing a circle on the paper secured to the ground.
• Create a new program file and name it "pointTurn." This makes the robot do a point turn so that it draws a smaller circle onto the paper. Follow Figure 3 for programming instruction. Download the program onto EV3 and run the program. Watch the robot make a point turn, tracing a small circle on the paper (make sure to give the robot enough space that the two circles drawn via "dragTurn" and "pointTurn" do NOT overlap).

  

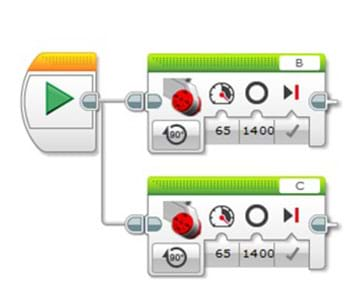
• For each circle drawn by the robot, measure the circumference and diameter and record them on a notepad. Measure the circumference by first tracing the circle with yarn and then, with a ruler, measuring the length of yarn needed to match the circle.

• Relate the circles drawn by the robot to real-life engineering examples. The "drag turn" circle drawn by the robot could be used to model a lawn sprinkler's path (the circumference that the water travels along). Use a ratio to make this representation; for example, 1 ft (real life) = 1 in (model). Pose a problem: If the lawn sprinkler needs to cover a radius of 5 feet, what circumference circle must the robot draw to accurately represent this model using the proposed ratio? What is the circumference and diameter of this drawn circle? The "point turn" circle drawn by the robot could model of the center of a basketball court (real life: diameter ~6 feet). Pose a similar problem with a scale ratio.

Vocabulary/Definitions

circumference: The length that makes up the closed curve of a circle.

diameter: Any straight line segment that passes through the center of a circle and whose endpoints are on the circle.

pi: A constant whose value is the ratio of any circle's circumference to its diameter.

radius: Any line segment from a circle's center to its perimeter.

Assessment

Pre-Activity Assessment

How accurate is your pi? Take an average of three pi values obtained from the three different-sized circles on the Pi Pre-Activity Worksheet. Compare this average value of pi to the known pi value: 3.14159... Ask students how close their averaged value of pi is to the known value of pi. If it is not exactly the same, what are some reasons for the difference? (Answers: Errors in measurement, imperfect circles.)

Activity Embedded Assessment

Different circles, same pi? After students complete the Pi Pre-Activity Worksheet and determine values of pi based on different-sized circles, ask them to predict the pi value of the circles that the robot draws.

Post-Activity Assessment

How accurate is the robot's pi? Take an average of two pi values obtained from the two different-sized circles drawn by the robot. Compare this average value of pi to the known pi value: 3.14159... How close was your calculated value? What do you think that says about the circles the robot has drawn? Do you think they are perfect circles? Why or why not? If the robot drew perfect circles, what could be another reason the averaged pi value is not the same as the known pi value? (Answer: Measurement errors.)

Troubleshooting Tips

1. If the robot does not travel the point turn as programmed, make sure that the surface of the ground is completely flat and the paper is taped securely to the floor (with no bumps).

• If that does not fix the problem, try programming the "pointTurn" using the help panel on the right side of the MINDSTORMS software.
• "Robot Educator" panel → "Common Palette" → "07. Point Turn" → "Programming Guide"

2. If the robot does not travel the drag turn as programmed, try using a "curve turn" as shown in the "Robot Educator" panel under "Common Palette."

Activity Scaling

• For upper grades, estimate the circumference of the robot's tires. Based on this value and the number of rotations that the robot travels, have students calculate a rough estimate of the circle's circumference. (This only works if the robot is programmed for exactly 1 round.)

Additional Multimedia Support

Show students an animated version of the image in the Introduction/Motivation section so they can see the unrolling a circle's circumference, illustrating the ratio π. This GIF file by John Reid is available at Wikimedia Commons at https://commons.wikimedia.org/wiki/File:Pi-unrolled.gif.

References

Copyright

Contributors

Supporting Program

Acknowledgements

This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.