Quick Look
Grade Level: 10 (9-11)
Time Required: 1 hour
Expendable Cost/Group: US $5.00
Group Size: 3
Activity Dependency: None
Subject Areas: Problem Solving, Science and Technology
NGSS Performance Expectations:

| HS-ETS1-2 |

Summary
Students take on the task of designing a container that holds exactly one spritz of water from a spray bottle. They measure the mass of the collected liquid, or spritz, and calculate how long it takes for the water to vaporize using a formula for an experimental rate of evaporation. After understanding the rate of evaporation, students iterate their designs and practice dimensional analysis to further analyze their data.Engineering Connection
Achieving rapid drying times are a crucial component of engineering. Adhesives and building materials, if applied in liquid form, must cure, harden, or dry before the next step in the manufacturing process. A more precise drying time may lead to a more efficient engineering process overall. Students are tasked with taking on the role of engineers to calculate drying time by examining the amount of water expelled from a spray bottle into a controlled space.
Learning Objectives
After this activity, students should be able to:
- Determine the mass of an unknown amount of liquid.
- Use iterative design to validate test results.
- Employ dimensional analysis to convert one unit to another with a given rate in mind.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-2. Design a solution to a complex real-world problem by breaking it down into smaller, more manageable problems that can be solved through engineering. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Design a solution to a complex real-world problem, based on scientific knowledge, student-generated sources of evidence, prioritized criteria, and tradeoff considerations. Alignment agreement: | Criteria may need to be broken down into simpler ones that can be approached systematically, and decisions about the priority of certain criteria over others (trade-offs) may be needed. Alignment agreement: | |
Common Core State Standards - Math
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Choose a level of accuracy appropriate to limitations on measurement when reporting quantities.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the core concepts of technology.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the attributes of design.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of engineering design.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Develop a device or system for the marketplace.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Optimize a design by addressing desired qualities within criteria and constraints.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Michigan - Math
-
Reason abstractly and quantitatively.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Choose a level of accuracy appropriate to limitations on measurement when reporting quantities.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Michigan - Science
-
Design a solution to a complex real-world problem by breaking it down into smaller, more manageable problems that can be solved through engineering.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- Student Worksheet
- spray bottle
To share with the entire class:
- glass or beaker of water (preferably one with a large surface area on the bottom)
- triple beam balance or electronic scale
- various material for construction:
- tape
- paper (either copy or construction)
- plastic wrap
- aluminum foil
- test tubes
- petri dishes
- paper towels
- sponges
- stop watches or timers to measure evaporation time
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cmu2-2343-paint-dry-design] to print or download.Pre-Req Knowledge
Ability to use an electronic scale or triple beam balance; familiar with dimensional analysis.
Introduction/Motivation
If you were to take a glass of water, weigh it, place it on a desk, and leave it for 24 hours, what would happen? We know that the water in the glass, if left for a long period of time, would eventually evaporate. However, what if we wanted to find out how much water evaporated in a day? Would you be able to make any qualitative observations about the water? What about quantitative?
To get started, let’s examine how we can measure a small amount of evaporation from our test glass. We can use the following formula to measure the rate of evaporation in grams per second:
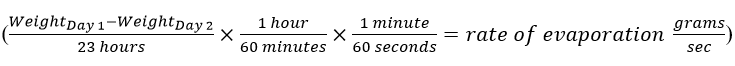
Understanding evaporation times are crucial component of engineering in industry. Adhesives and liquids applied to a project must cure, harden, or dry before the next step in the manufacturing process. Faster drying times lead to more efficient engineering processes (and, as is often in the case of industry, money saved), which brings us to your task: design a container to capture water expelled from a spray bottle and then measure that expelled amount.
Take on the role of engineers and assist a local manufacturing facility that designs and manufactures sports equipment. Part of the facility’s process requires finishing their produced sporting goods with paint. This process requires the use of as little paint as possible and to achieve a fast drying time. If the paint does not dry properly, we may see imperfections emerge that may necessitate additional, costly painting cycles. As engineers, you will work in groups to not only calculate the drying time, but also to design an optimal container to capture water from a spray bottle. By building this container, you can then estimate the amount of time it takes for your projects at the sports equipment facility to dry.
Procedure
Before the Activity
- Display a glass or beaker of water on a desk.
- Use an electronic balance to measure the glass of water between two time periods; (for example, during a 24 hour period between the start of the activity and the next day.) Make a note of the glass or beaker and its contents one day before you begin the activity.
- See Additional Teacher Resources for assistance with developing questions for this activity.
With the Students
- Divide the class into groups of three or four students each.
- Introduce the activity, the engineering challenge, and (as an optional extension) show a video of a manufacturing painting process, such as Commercial Vehicle Paint systems from Indivizual Media or Robots Painting Tesla Model S by I Love Robotics.
- Refer to the glass or beaker from the previous class. Ask students what may have happened to the water level in the glass or beaker.
- Weigh the water and give students both the previous day’s weight and today’s weight.
- Ask students to work in groups to discuss how they can tell how much water evaporates in an hour, based on knowing the previous and current weight as well as the time difference between measuring periods.
- Guide students through the process of dimensional analysis (see Figure 1) as they discuss in groups.
- Write each group’s final answer as to how many milliliters of water evaporates in 1 hour.
- Spray a single spritz of water in the air; compare this to a paint applicator that applies a powder coat or spray paint to a piece of sports equipment.
- Ask students how much water they think they released into the air— how might they calculate the amount? If they knew how much water was expelled from the water bottle, they could also calculate the drying time.
- Show students the various supplies and measuring device you have available for them to use.
- Distribute copies of the Student Worksheet. Give students their mission of calculating the drying time of one spritz of water; infer they must first know the weight of a spritz of water.
- Students then work on building a device to catch a spritz of water.
- Students test their device and iterate their device. Remind students that exact drying times are required within a manufacturing setting; it is important for manufacturing engineers to iterate their designs so they can calculate exact drying times.
- Students measure the weight of the water and calculate the drying time.
- Regroup for a class discussion about their calculated drying time of a spritz of water.
Vocabulary/Definitions
dimensional analysis: A method of analysis in which physical quantities are expressed in terms of their fundamental dimensions that is often used when there is not enough information to set up precise equations.
evaporation: The process of turning from liquid to vapor.
Assessment
Pre-Activity Assessment
Brainstorming: In small groups, have students predict what will happen to a glass of water if it is left out overnight. Remind them to be specific when explaining quantifiable things and explain their reasoning.
Activity Embedded Assessment
Class Discussion: Students report their final evaporation rate for one spritz of water including the methods they used to arrive at that number. Each group is likely to have a different number; ask students why this number may not be the same from each group.
Post-Activity Assessment
Exit Ticket: Have students complete an exit ticket asking them to write down three things they learned from the activity, two difficulties they had to overcome, and one moment they felt successful.
Troubleshooting Tips
The largest obstacle to overcome is that one spritz of water is likely not detectable using an average electronic scale. Prepare to guide students towards alternate ways of discovering the weight of an average spritz of water. See the Additional Teacher Resources document for a walkthrough of the design process.
Activity Extensions
After students have a time for a ‘coat’ of water to dry, have students calculate how many ‘coats’ of water could be applied to their container in the course of… an hour, 4 hours, 8 hours, etc.
Activity Scaling
- For lower grades, provide students with fewer materials for their building challenge. Also consider scaffolding the concept that taking an average of a collection of spritzes would result in the measurement of a single spritz.
- For higher grades, have students take temperature and/or humidity into account for their drying time. Students may wish to investigate ways to control either of the aforementioned variables.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students explore the basic characteristics of polymers through the introduction of two polymer categories: thermoplastics and thermosets. During teacher demos, students observe the unique behaviors of thermoplastics.

Students examine in detail the water cycle components and phase transitions, and then learn how water moves through the human-made urban environment. Students show their understanding of the process by writing a description of the path of a water droplet through the urban water cycle, from the dropl...
Copyright
© 2019 by Regents of the University of Colorado; original © 2018 Central Michigan UniversityContributors
Andy FrischSupporting Program
Research Experience for Teachers Program, Central Michigan UniversityAcknowledgements
This curriculum was based upon work supported by the National Science Foundation under RET grant no. EEC 1542368— Research Experience for Teachers through Central Michigan University. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Last modified: February 21, 2020





User Comments & Tips