Quick Look
Grade Level: 7 (6-8)
Time Required: 1 hour
Expendable Cost/Group: US $5.00 In addition, a non-expendable cost is a $300 LEGO® MINDSTORMS® EV3 kit for a teacher demo; one is sufficient and it is highly reusable.
Group Size: 2
Activity Dependency:
Subject Areas: Algebra, Measurement, Number and Operations
Summary
Students discover the mathematical constant phi, the golden ratio, through hands-on activities. They measure dimensions of "natural objects"—a star, a nautilus shell and human hand bones—and calculate ratios of the measured values, which are close to phi. Then students learn a basic definition of a mathematical sequence, specifically the Fibonacci sequence. By taking ratios of successive terms of the sequence, they find numbers close to phi. They solve a squares puzzle that creates an approximate Fibonacci spiral. Finally, the instructor demonstrates the rule of the Fibonacci sequence via a LEGO® MINDSTORMS® EV3 robot equipped with a pen. The robot (already created as part of the companion activity, The Fibonacci Sequence & Robots) draws a Fibonacci spiral that is similar to the nautilus shape.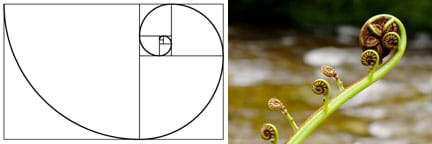
Engineering Connection
Phi is arguably one of the most important mathematical constants. From the great pyramids to the Parthenon, this number appears in the shapes and scales of many engineering designs and architectural feats. In art, this constant is used to quantify aesthetic beauty, such as in da Vinci's Mona Lisa, or even the face of a beautiful person. This activity builds upon the omnipresence of this number to introduce students to discrete mathematics, and extends the idea of a mathematical sequence to basic programming using the EV3 MINDSTORMS software.
Learning Objectives
After this activity, students should be able to:
- Explain the general term of the Fibonacci sequence.
- Describe examples of phi in nature.
- Identify phi as the limit of the ratio of terms of the Fibonacci sequence.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Fluently divide multi-digit numbers using the standard algorithm.
(Grade
6)
More Details
Do you agree with this alignment?
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.
(Grade
6)
More Details
Do you agree with this alignment?
-
Investigate patterns of association in bivariate data.
(Grade
8)
More Details
Do you agree with this alignment?
-
Recognize that sequences are functions, sometimes defined recursively, whose domain is a subset of the integers.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Apply design concepts, principles, and processes through play and exploration.
(Grades
Pre-K -
2)
More Details
Do you agree with this alignment?
-
Explain how various relationships can exist between technology and engineering and other content areas.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
-
Design solutions by safely using tools, materials, and skills.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
Use ratio reasoning to convert measurement units; manipulate and transform units appropriately when multiplying or dividing quantities.
(Grade
6)
More Details
Do you agree with this alignment?
-
Fluently divide multi-digit numbers using the standard algorithm.
(Grade
6)
More Details
Do you agree with this alignment?
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Investigate patterns of association in bivariate data.
(Grade
8)
More Details
Do you agree with this alignment?
-
Recognize that sequences are functions, sometimes defined recursively, whose domain is a subset of the integers.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- ruler
- pencils
- calculator
- laminated Fibonacci squares puzzle made from poster board (use the Squares Puzzle Template)
- Brainstorming Squares, one copy per pair of students
- Math Adventurers Worksheet, one copy per pair of students
To share with the entire class:
- several laminated copies the three-page Natural Pictures attachment, enough so each group can have at least one picture at any one time
For the robot teacher demonstration:
- LEGO EV3 kit (buildable and programmable robot), available at https://shop.lego.com/en-US/LEGO-MINDSTORMS-EV3-31313, $349.99, with robot constructed and programmed as in The Fibonacci Sequence & Robots activity
- large sheets of paper
- tape, to secure paper to the floor and a marker to the robot
- marker
Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT kit instead of EV3
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_phi_activity1] to print or download.Pre-Req Knowledge
Ability to perform division, and an understanding of the basic concept of a function.
Introduction/Motivation
The mathematical constant phi has been studied since at least 300 BCE, when it was defined by Greek mathematician Euclid. The formalization of phi may have been motivated by its presence in the pentagram, a common religious symbol at that time. It is found all over in nature, from snail shells and flower seed heads to many plant patterns such as those in pineapples, ferns and pinecones. And, it plays a key role into Western aesthetics and architecture. Phi, as a ratio, features prominently in works of da Vinci and Dali. Also, phi has been observed in many areas of mathematics, from geometry such as regular pyramids, to number theory, such as Lagrange's approximation theorem.

During today's activity, you will "discover" phi in two ways: through a simulation and through examination of specific mathematical objects.
The mathematical source of phi, the Fibonacci sequence, is a sequence formed by adding two successive terms to get the next term. (If necessary, use the classroom board or an overhead projector to show students how to generate the next terms.) If I begin with 0 and 1, who can tell me the next few numbers in the sequence? (Answer: 1, 2, 3, 5.)
In the squares puzzle part of this activity, you can solve this puzzle in a variety of ways by making increasingly larger rectangles with side lengths terms of the Fibonacci sequence. Next, you will think about how these rectangles relate to each other. It turns out that the ratio of successive terms of the Fibonacci sequence is phi.
(Assuming you have conducted the companion activity, The Fibonacci Sequence & Robots...) Now, let's think about the robots that we have programmed with the Fibonacci sequence. How did the robot follow your orders (the program) when completing the Fibonacci sequence? Did the robot exactly follow your orders? How precise did you have to be with your programming for the robot? (Expect students to be able to recognize that the robot does only exactly what is it told to do; it is incapable of making addition errors, for example.) This type of precision is necessary by engineers when programming robotic technologies, such as robotic arms used in foundries or surgeries. Today, we are also going to program a robot to follow the phi ratio and see what happens.
Procedure
Before the Activity
- Gather materials and make copies of the Brainstorming Squares, and Math Adventurers Worksheet (one each for every two students).
- Print out and laminate enough copies of the three-page Natural Pictures document so that each group can have at least one picture at any given time.
- Using the Squares Puzzle Template, cut and laminate poster board pieces, labeling the size on each piece, making enough for one puzzle per group.
- Construct and program the LEGO EV3 robot, as provided in The Fibonacci Sequence & Robots activity.
- Use tape to secure large sheets of paper to the floor for the robot drawing.
- Use tape to attach the marker to the robot so that the marker draws on the floor as the robot moves.
With the Students
- Divide the class into pairs of students.
- Distribute to each group: a ruler, calculator, brainstorming squares sheet, worksheet, squares puzzle, and one picture.
- Start by having teams do the Brainstorming Squares activity by following the instructions on the sheet, as described in the Assessment section.
- Introduce the concept of a mathematical constant, specifically phi, as presented in the Introduction/Motivation section. Note: Students may already be familiar with the constant pi, and this can be a good starting point for further discussion on constants.
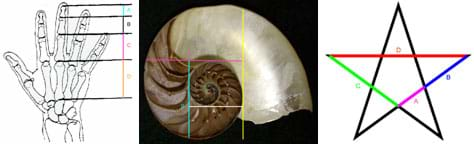
Figure 1. The three "natural pictures" students measure to calculate the golden ratio, phi. - Display each of the three "natural pictures" to the entire class and name each: the human hand, the nautilus, and the five-pointed star (see Figure 1). Each of these objects can be considered as harboring the golden ratio, phi. Have student teams complete Part 1 of the worksheets, following these steps:
- Have each team designate a measurer and a recorder.
- Looking at a picture, the measurer uses a ruler to measure the lengths, A, B, and C, and relays these numbers to the recorder.
- The recorder writes down the measurements on the worksheet, and uses a calculator to determine the ratios of the measured lengths, filling in the rest of Part 1 of the worksheet.
- The teams trade pictures and repeat this activity until all groups have considered all three pictures.
- Lead a class discussion to compare results. Ask: What was the trend of the ratios found in the pictures?
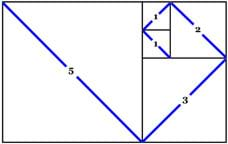
Figure 2. The completed squares puzzle, which is a tiling of squares whose side dimensions are successive Fibonacci sequence numbers. The diagonal lines through each square approximate the golden spiral line shape. - Introduce the concept of a mathematical sequence, specifically the Fibonacci sequence.
- Refer to the history and information provided in the Introduction/Motivation section.
- Go through the first four or five terms of the sequence with the class, and construct the first two or three pieces of the squares puzzle.
- Let the pairs complete Part 2 of the worksheet together, finding more terms of the Fibonacci sequence and as well as the ratios of successive terms.
- Have the students complete the squares puzzle (see Figure 2).
- Bring the class back together for a final discussion of their worksheet answers and the squares puzzle. Relate the presence of phi in this mathematical object. Discuss the relationship of the lengths of the sides of the squares in the puzzle and the Fibonacci sequence.
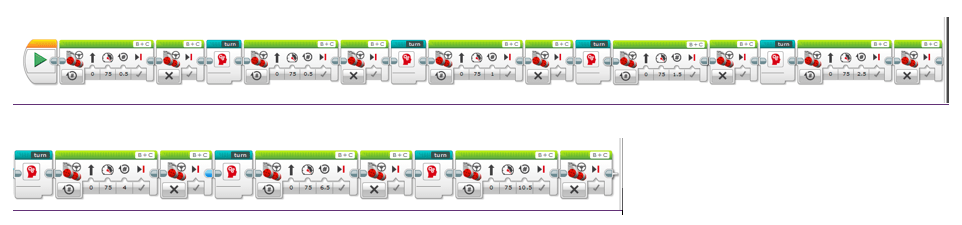
Figure 3. An example LEGO MINDSTORMS programming for a LEGO EV3 robot, showing a series of programming blocks, specifically Motor Move Blocks connected via Sequencing Blocks. This particular program is designed to move a LEGO EV3 robot along a Fibonacci spiral. The Motor Move Blocks are programmed to use distances according to the Fibonacci sequence.

- Demonstrate the LEGO EV3 robot moving according to the rule of the Fibonacci sequence. If possible, display the amended MINDSTORMS code from the companion activity (The Fibonacci Sequence & Robots) that has the robot proceed distances dictated by the Fibonacci sequence along with right-angle turns, see Figure 3. If students are unfamiliar with the software, explain the components of the program. Then, conduct the demonstration:
- Set up the robot on sheets of paper taped to the floor, with the marker attached so that a line is drawn as the robot moves, see Figure 4.
- Ask students to predict what shape the robot will draw.
- Run the program as the class observes. (The robot should draw a Fibonacci spiral.)
- Discuss how, using the robot, we can visually perceive phi embedded in the Fibonacci sequence.
- Conclude with the post-activity assessment activities suggested in the Assessment section.
Vocabulary/Definitions
limit of a sequence: The number approached by the terms of a sequence as one proceeds through the order of the sequence.
phi: A mathematical constant of approximately 1.61803, calculated by taking the ratio between successive Fibonacci sequence terms. The higher you go in the Fibonacci sequence, the more closely the ratio between the two successive numbers approximates phi. Also called the "golden ratio." (Pronounced: "fee")
sequence (numerical): An ordered set of numbers arranged according to a rule.
term: One of the numbers in a sequence.
Assessment
Pre-Activity Assessment
Brainstorming Squares: Divide the class into groups of two. Pass out a copy of Brainstorming Squares and a ruler to each group. Instruct the paired students to look for mathematical patterns within the measurements of the squares in the spiral drawing on the handout. Give students five minutes to come up with three measurement-based observations of how the squares relate to one another. After the five minutes are up, have a few groups share with the class what they found out. Tell the class that by the end of this activity, they will know exactly how these squares relate to each other!
Activity Embedded Assessment
Worksheet: Have each student pair complete the Math Adventures Worksheet, making the measurements and calculations, and answering the questions. Review their answers to gauge their comprehension of the material covered.
Prediction: To see if students are following along, after explaining the robot's program, ask students to predict the shape that they expect the robot to draw.
Post-Activity Assessment
Tuning the Sequence: Challenge students to think about would happen if we wanted the robot to travel a different initial distance. Would it change the ratio that previously gave us phi? (Answer: No! Even though the individual numbers would change, the ratios would be proportionally the same and should still approximate phi. Remember, phi is determined by the ratio of the terms, and that is independent of initial conditions.)
Engineering Phi: Have students start by thinking about phi in nature and then brainstorm engineering designs that mimic nature and the golden ratio as found nature (called biomimicry). For example, spiral fans and pumps that reflect the same shape as a nautilus have been found to increase the efficiency of energy, and buildings. As an example, see "PaxFan: An Effective Spiral Fan" on the Treehugger Discovery Company website at https://www.treehugger.com/interior-design/paxfan-an-effective-spiral-fan.html
Troubleshooting Tips
Test the robot's program before class, and make sure the paper is large enough for the robot to draw at least a couple turns of the spiral.
Activity Extensions
In advance of this activity, conduct the The Fibonacci Sequence & Robots companion activity, in which student teams program a LEGO EV3 robot to move based on the Fibonacci sequence of numbers, helping them to visualize how quickly the numbers in the sequence grow.
The golden ratio is mostly about aesthetics. Have students choose one structure or technology and pretend they work for an engineering firm that has been commissioned to improve the design in some way. Have them write paragraphs about how they would improve the aesthetics of the design, specifically using phi.
Activity Scaling
For upper grades, have students construct and program the robot, as in the The Fibonacci Sequence & Robots activity, using the concept of variables developed in that activity. Also, discuss how phi appears in the ratios of the terms of the Fibonacci sequence independent of the initial conditions. Illustrate this using the robot, by changing starting distances.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Using the LEGO® EV3 robotics kit, students construct and program robots to illustrate and explore the Fibonacci sequence. By designing a robot that moves based on the Fibonacci sequence of numbers, they can better visualize how quickly the numbers in the sequence grow.
References
Livio, Mario. The Golden Ratio. New York, NY: Broadway Books, 2002.
Obara, Samuel. "Golden Ratio in Art and Architecture." Department of Mathematics Education. The University of Georgia. Accessed December 22, 2011. (Great history, explanations and visual aids for teaching about the golden ratio and golden spiral.) http://jwilson.coe.uga.edu/EMT668/EMAT6680.2000/Obara/Emat6690/Golden%20Ratio/golden.html
Copyright
© 2013 by Regents of the University of Colorado; original © 2009 Polytechnic Institute of New York UniversityContributors
Nicole AbaidSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: April 24, 2019






User Comments & Tips