Quick Look
Grade Level: 7 (6-8)
Time Required: 2 hours
(can be split into two 60-minute sessions)
Expendable Cost/Group: US $3.00 In addition, the activity uses a non-expendable (reusable) $300 LEGO® MINDSTORMS® EV3 kit; one is sufficient for the entire class.
Group Size: 5
Activity Dependency: None
Subject Areas: Algebra, Problem Solving, Science and Technology
NGSS Performance Expectations:

| HS-ETS1-4 |

Summary
Using the LEGO® EV3 robotics kit, students construct and program robots to illustrate and explore the Fibonacci sequence. Within teams, students are assigned roles: group leader, chassis builder, arm builder, chief programmer, and Fibonacci verifier. By designing a robot that moves based on the Fibonacci sequence of numbers, they can better visualize how quickly the numbers in the sequence grow. To program the robot to move according to these numbers, students break down the sequence into simple algebraic equations so that the computer can understand the Fibonacci sequence.Engineering Connection
The Fibonacci sequence is widely used in engineering applications including computer data structures and sorting algorithms, financial engineering, audio compression, and architectural engineering. The Fibonacci sequence can be seen in nature in the spirals of a sunflower's seeds and the shape of a snail's shell. The Fibonacci sequence is also the basis for the golden ratio, which is a classical proportion used in architecture and design.
Thanks to engineers, robots have migrated from factory shop floors (as industrial manipulators) to outer space (as interplanetary explorers), hospitals (as minimally invasive surgical assistants), homes (as vacuum cleaners and lawn mowers), and battlefields (as unmanned air, underwater, and ground vehicles). This activity builds upon students' innate fascination with robotics, exposing them to the notion of sequences and developing their critical thinking skills.
Learning Objectives
After this activity, students should be able to:
- Describe number sequences.
- Illustrate Fibonacci sequence using LEGO EV3.
- Verify terms of sequence using measurement by robot motion.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-4. Use a computer simulation to model the impact of proposed solutions to a complex real-world problem with numerous criteria and constraints on interactions within and between systems relevant to the problem. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Use mathematical models and/or computer simulations to predict the effects of a design solution on systems and/or the interactions between systems. Alignment agreement: | Both physical models and computers can be used in various ways to aid in the engineering design process. Computers are useful for a variety of purposes, such as running simulations to test different ways of solving a problem or to see which one is most efficient or economical; and in making a persuasive presentation to a client about how a given design will meet his or her needs. Alignment agreement: | Models (e.g., physical, mathematical, computer models) can be used to simulate systems and interactions—including energy, matter, and information flows—within and between systems at different scales. Alignment agreement: |
Common Core State Standards - Math
-
Fluently divide multi-digit numbers using the standard algorithm.
(Grade
6)
More Details
Do you agree with this alignment?
-
Know the formulas for the area and circumference of a circle and use them to solve problems; give an informal derivation of the relationship between the circumference and area of a circle.
(Grade
7)
More Details
Do you agree with this alignment?
-
Recognize that sequences are functions, sometimes defined recursively, whose domain is a subset of the integers.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Apply design concepts, principles, and processes through play and exploration.
(Grades
Pre-K -
2)
More Details
Do you agree with this alignment?
-
Explain how various relationships can exist between technology and engineering and other content areas.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
-
Design solutions by safely using tools, materials, and skills.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
-
Explain how technology and engineering are closely linked to creativity, which can result in both intended and unintended innovations.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
New York - Science
-
Use a computer simulation to model the impact of proposed solutions to a complex real-world problem with numerous criteria and constraints on interactions within and between systems relevant to the problem.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- Windows PC
- LEGO MINDSTORMS robot, such as EV3 Core Set (5003400) at https://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3
- measuring tape, in metric units
- marker
- Fibonacci Robots Worksheet, one per student
- Robot Building Guide, one per team (or printer fewer copies and have teams share)
- Fibonacci Homework Handout, one per student
To share with the entire class:
- 10 sheets of copy paper (a few more sheets may be needed)
- tape
Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT Base set instead of EV3.
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_fibonacci_activity1] to print or download.Pre-Req Knowledge
Familiarity with LEGO robot EV3 kits.
Introduction/Motivation

A sequence is an ordered list of numbers, in which each number is referred to as a term. Many types of sequences exist. Some are named after the type of mathematical operators being used, such as a square or cube sequence. Some are named after the type of term progression, such as a harmonic sequence or a geometric sequence. And some are named after the person who established the sequence, such as Fourier, Farey or Fibonacci.
In Europe in the middle ages (1200s), Roman numerals were used for mathematics and accounting. Then Leonardo of Pisa, known as Fibonacci, introduced the use of Arabic numerals (0-9). He learned of this different numbering system from his travels to foreign countries as a child. He said, "With these nine figures and the sign 0... any number may be written." Adopting this system resulted in an important and dramatic simplification in the way numbers were written in Europe. Fibonacci also introduced a specific sequence of numbers to the Western world in his 1202 book, Liber Abaci (translation: Book of Calculation). Although the description of the sequence seems difficult, it is one of the easiest sequences to understand.
Let's see how the Fibonacci sequence works. (Use the classroom board or an overhead projector to show students the following explanation.) The sequence starts with two numbers 0 and 1. To find the next number of the sequence, we add the two previous numbers: in this case, 0 + 1 = 1. Now we have the sequence 0, 1, 1. To find the next number of the sequence, we repeat the above procedure using what are now the last two terms in the sequence: 1 + 1 = 2. Now we have the sequence 0, 1, 1, 2. We can repeat this procedure to get a sequence that continues forever to, what mathematicians call, infinity.
The Fibonacci sequence has attracted significant attention because it shows up in nature in the form of spirals, in such things as sunflowers and snail shells. It is recognized by engineers who are inspired by the unique spiral shape to design fans and pumps that increase the efficiency of energy and buildings. This sequence is also used to generate the famous golden ratio, which appears in engineering and architecture from the great pyramids to the Parthenon, and in art, as shown in the shape of Mona Lisa's face.
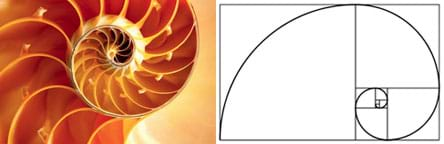
Today, you will work as engineers together in teams, using the LEGO EV3 robotics kit to explore the Fibonacci sequence! You will be given a job and will learn about the importance of sequences while building and programming robots that use the Fibonacci sequence!
Procedure
Before the Activity
- Gather materials and make copies of the Fibonacci Robots Worksheet (one per student), Robot Building Guide (one per team) and Fibonacci Homework Handout (one per student).
- So that the marker does not make marks on the floor in the area where you plan to operate the robot, make a "street" with pieces of paper oriented the long way and connected using tape. Start out with 10 pieces of paper, but be ready to add length if students write programs that cover more distance!
With the Students
- Divide the class into groups of four or five students each.
- Within teams, assign four different jobs: Group Leader, Chassis Builder, Pen Attachment Builder, Chief Programmer, and Fibonacci Verifier. (Alternatively, let the students in each group choose the jobs they want.) The job descriptions are as follows:
- Group Leader: Locates parts needed for construction of robot chassis and arm, and assists the Chief Programmer with MINDSTORMS® EV3.
- Chassis Builder: Constructs robot according to the Robot Building Guide. Any small, mobile robot is okay, so modifications are encouraged. Remember, engineers love to brainstorm, come up with designs, test their designs, and then rebuild!
- Pen Attachment Builder: Devises a way to attach a pen to the robot using LEGO and tape so that the pen draws on the ground as the robot drives.
- Chief Programmer: Writes a program that moves the robot according to the Fibonacci sequence. For example, the third term is 1, so the robot's wheels should move 1 full rotation and then stop. The fourth term is 2, so the robot's wheels should only move 2 full rotations and then stop.
- Fibonacci Verifier: Assists the Chief Programmer, verifies that the robot moved according to the Fibonacci sequence, and records data.
- Build the robot and start programming.
- The Group Leader locates and brings the pieces needed by the Chassis Builder, makes sure that all other group members are on task, and provides support when needed.
- The Chassis Builder constructs the robot, using the Robot Building Guide as a starting point.
- The Pen Attachment Builder conceptualizes the arm, talks it over with the Group Leader, and starts to build when the chassis is finished. While the chassis is being built, the Pen Attachment Builder locates the pieces necessary for the arm. If the chassis still is not built, the Pen Attachment Builder helps the Chassis Builder.
- The Chief Programmer starts with programming in MINDSTORMS® EV3, and begins by first drawing out the program on a sheet of paper.
- The Fibonacci Verifier computes the first 10 terms of the Fibonacci sequence. Then, the Fibonacci Verifier works with the Chief Programmer, giving suggestions and working as a team.
- Build the robot's pen attachment.
- The Group Leader works with the Chief Programmer and the Fibonacci Verifier.
- The Group Leader works with the Chief Programmer and the Fibonacci Verifier.
- The Pen Attachment Builder constructs the pen attachment and takes the lead for building, with the Chassis Builder for support.
- The Chief Programmer continues programming.
- The Fibonacci Verifier continues programming with the Chief Programmer.
- Place the marker in the robot's arm and test to see if the marker draws on the "street" when the robot moves.
- Teach the robot.
- Program the robot to run on the "street" using the attached EV3 program.
- The Fibonacci Verifier marks with a pen on the street every time the robot stops. The Fibonacci Verifier measures the distance between adjacent marks. The distance should be increasing according to the terms of the Fibonacci sequence. The Fibonacci Verifier records all data and verifies the program worked correctly. If incorrect, make programming adjustments and try again.
- For extra credit: If your programming did not use variables, re-write it so that the robot can compute and move according to the Fibonacci sequence infinitely!
- Hand out the worksheets and have students complete the questions and hand them in for grading.
- For homework: Pass out the homework handout to have students use their math skills to approximate phi, "the golden ratio," from the Fibonacci sequence, as described in the Assessment section.
Vocabulary/Definitions
infinity: Unable to be counted, unlimited.
robotics: The science or study of the technology associated with the design, fabrication, theory, and application of robots.
sequence: (noun) An ordered set of numbers, shapes or other mathematical objects, arranged according to a rule.
term: One of the numbers in a sequence.
variable: A symbol used to represent a value.
Assessment
Pre-Activity Assessment
What's a Robot? Have students discuss and explain the robot components necessary for moving in a pattern and drawing its trajectory path. Components include items such as the brain (EV3 brick), motors, assorted LEGO pieces, attachments for pens or markers to draw, and a program to allow it to operate autonomously.
Activity Embedded Assessment
What Affects the Distance Traveled by the Robot? Have students hypothesize what factors might affect the movement of the robot as it moves through the program and completes the sequence. Possible factors: wheel size, initial rotation value, programs that include steering or pivot/swing turns, etc.
Post-Activity Assessment
Summary Worksheet: Have students complete the Fibonacci Robots Worksheet by answering the analysis questions. Review their answers to gauge their comprehension of the material covered.
Math Homework: As homework for this activity (and/or as a lead-in to the companion activity, Discovering Phi: The Golden Ratio), have students complete the Fibonacci Homework Handout in which they calculate an important constant called "phi," or the "golden ratio."
Troubleshooting Tips
If you do not have enough room on the floor for the robot to travel, use one-half or one-quarter rotations instead of full rotations of the robot wheels.
Activity Extensions
Conduct the companion activity, Discovering Phi: The Golden Ratio, which uses the same LEGO EV3 kit and robot programming for a teacher demonstration of the Fibonacci spiral.
Have students research how the Fibonacci sequence relates to right triangles.
Have students research where the Fibonacci sequence is found in nature, art, architecture, etc. For example: the proportions in Leonardo da Vinci's Mona Lisa, the rectangles in Piet Mondrian's Composition 10, and the spirals on the ceiling of the Grand Ballroom at the Omni William Penn Hotel in Pittsburgh PA.
Have students think about and/or research how the Fibonacci sequence could be used in engineering designs. For example, spiral fans and pumps of the shape described by a Fibonacci spiral are known to increase the efficiency of energy and buildings. Research by searching on "biomimicry, spiral, shell."As an example, see "PaxFan: An Effective Spiral Fan" on the Treehugger Discovery Company website at https://www.treehugger.com/green-design-4846020
Activity Scaling
- For lower grades, have students simply create a chain of motor blocks that move the robot by pre-determined terms of the Fibonacci sequence.
- For upper grades, require that students only use variables in their programming to produce the terms of the Fibonacci sequence for the robot, and display the recent term on the EV3 brick. Have students move the robot to the Fibonacci spiral.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students discover the mathematical constant phi, the golden ratio, through hands-on activities. They measure dimensions of "natural objects"—a star, a nautilus shell and human hand bones—and calculate ratios of the measured values, which are close to phi.
References
Eather, Jennifer. Published 2011. A Maths Dictionary for Kids. Accessed December 22, 2011. (Source of mathematical definitions) http://www.amathsdictionaryforkids.com/
Fibonacci. Platonic Realms Interactive Mathematics Encyclopedia, Math Academy, Radford VA. Accessed January 27, 2009. http://platonicrealms.com/encyclopedia/
Fibonacci number in nature. Wikipedia. The Free Encyclopedia. Accessed December 22, 2011. (Examples: tree and leaf branching, pineapple, artichoke, fern, pinecone, shell spirals, rabbit breeding, sunflower seeds, wave curls, honeybee family tree) http://en.wikipedia.org/wiki/Fibonacci_number#In_nature
The LEGO® Group. LEGO®, MINDSTORMS®, the Brick and EV3 configurations are trademarks of the LEGO Group. Accessed January 27, 2009. http://mindstorms.lego.com
Monteferrante, Sandra. "Leonardo of Pisa: Bunny Rabbits to Bull Markets." Loci: Convergence, The MAA Mathematical Sciences Digital Library, The Mathematical Association of America. Accessed December 22, 2011. (Good information on history, Fibonacci numbers, patterns, golden ratio, phyllotaxis-the study of plant patterns, and Elliott waves; also look at Golden Spiral entry) http://mathdl.maa.org/mathDL/46/?pa=content&sa=viewDocument&nodeId=2242
Copyright
© 2013 by Regents of the University of Colorado; original © 2009 Polytechnic Institute of New York UniversityContributors
Nicole Abaid; Alexander Kozak; Vikram Kapila; Russell HolsteinSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: October 16, 2020




User Comments & Tips