Quick Look
Grade Level: 5 (4-6)
Time Required: 1 hours 45 minutes
(60 minutes for activity + 45 minutes for data analysis/follow-up)
Expendable Cost/Group: US $0.00 The activity uses non-expendable (reusable) LEGO MINDSTORMS robots and software; see the Materials List for details.
Group Size: 3
Activity Dependency: None
Subject Areas: Algebra, Data Analysis and Probability, Measurement
NGSS Performance Expectations:

| 3-5-ETS1-3 |
Summary
Students strengthen their communication skills about measurements by learning the meaning of base units and derived units, including speed—one of the most common derived units (distance/time). Working in groups, students measure the time for LEGO® MINDSTORMS® robots to move a certain distance. The robots are started and stopped via touch sensors and programmed to display the distance traveled. Using their collected data, students complete a worksheet to calculate the robots' (mean/average) speeds at given motor powers.
Engineering Connection
Communicating measurements is one of the most important everyday engineering and math literacy tasks. In today's cutting-edge technical applications, new types of units are frequently created to highlight a process of interest, such as a unit of speed created from the units of distance and time (foot per nanosecond, terafurlongs per fortnight, mickey per second) or a unit of density created from the units of length and mass. Base units are usually fundamental units for properties such as mass and length, and derived units are generated from combinations of units to describe the most basic observable properties of an object or situation. Understanding that base units make up derived units is essential to being a competent engineer. Another way to think about it is that derived units (such as mph) are rates of change between base units (miles = distance, hour = time). Derived units are important in science and engineering for measuring physical phenomena, and are created by performing arithmetic (such as division) on the corresponding base units.
Learning Objectives
After this activity, students should be able to:
- Define speed using the speed equation: speed = distance ÷ time.
- Identify and explain a unit of speed.
- Generate a unit of speed by combining different units of length and time.
- Calculate the speed of an object moving in a straight line by dividing the measured distance traveled by the measured time elapsed.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
3-5-ETS1-3. Plan and carry out fair tests in which variables are controlled and failure points are considered to identify aspects of a model or prototype that can be improved. (Grades 3 - 5) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Plan and conduct an investigation collaboratively to produce data to serve as the basis for evidence, using fair tests in which variables are controlled and the number of trials considered. Alignment agreement: | Tests are often designed to identify failure points or difficulties, which suggest the elements of the design that need to be improved. Alignment agreement: Different solutions need to be tested in order to determine which of them best solves the problem, given the criteria and the constraints.Alignment agreement: | |
Common Core State Standards - Math
-
Attend to precision.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
(Grade
4)
More Details
Do you agree with this alignment?
-
Fluently divide multi-digit numbers using the standard algorithm.
(Grade
6)
More Details
Do you agree with this alignment?
-
Solve unit rate problems including those involving unit pricing and constant speed.
(Grade
6)
More Details
Do you agree with this alignment?
-
Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities.
(Grade
6)
More Details
Do you agree with this alignment?
-
Describing the nature of the attribute under investigation, including how it was measured and its units of measurement.
(Grade
6)
More Details
Do you agree with this alignment?
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the characteristics and scope of technology.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of engineering design.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the attributes of design.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
Attend to precision.
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
-
Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
(Grade
4)
More Details
Do you agree with this alignment?
-
Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities.
(Grade
6)
More Details
Do you agree with this alignment?
-
Solve unit rate problems including those involving unit pricing and constant speed.
(Grade
6)
More Details
Do you agree with this alignment?
-
Fluently divide multi-digit numbers using the standard algorithm.
(Grade
6)
More Details
Do you agree with this alignment?
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Describing the nature of the attribute under investigation, including how it was measured and its units of measurement.
(Grade
6)
More Details
Do you agree with this alignment?
New York - Science
-
Plan and carry out fair tests in which variables are controlled and failure points are considered to identify aspects of a model or prototype that can be improved.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- LEGO MINDSTORMS EV3 robot, such as EV3 Core Set (5003400) at https://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3
- LEGO MINDSTORMS Education EV3 Software 1.2.1, free online, you have to register a LEGO account first; at https://www.lego.com/en-us/mindstorms/downloads/download-software
- computer, loaded with EV3 1.2.1 software
- Forward_Timing_Bot.ev3 (ev3), a LEGO MINDSTORMS EV3 program
- Pre-Activity Evaluation, one per student
- Speedbot Data Worksheet, one per group
- Speed Equation Worksheet, one per student
- Post-Activity Evaluation, one per student
- stopwatch or timer
- (optional) calculator(s)
Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:
- LEGO MINDSTORMS NXT robot, such as the NXT Base Set
- LEGO MINDSTORMS Education NXT Software 2.1
- computer, loaded with NXT 2.1 software
- Forward_2_2.rbt (rbt)
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_speedbot_activity1] to print or download.Pre-Req Knowledge
Students should be familiar with metric units of length and various units of time. Students should also be comfortable performing long division by hand using integer divisors up to three digits. If scaffolding is necessary for different learning levels and abilities, students can also use calculators to verify answers.
Introduction/Motivation
Speed affects our lives every day because it dictates how long it takes to travel a certain distance. Typically when traveling great distances, we want to travel at high speed so it doesn't take a long time to arrive at our destinations. When during your day are you aware of the speed of something?
In the world of engineering, speed is a very important design consideration. Engineers are continually trying to increase the speed of cars, airplanes and spacecraft. Currently, one of the biggest challenges facing engineers in space travel is the time it takes to cover the great distances of outer space. In order to cover these great distances within a reasonable amount of time, we must go faster! Another challenge involving speed is in robotics and bioengineering. For example, to design prosthetic limbs so they are useful, we want their movements to be speedy (almost instantaneous), in order to replicate the movement of natural arms, legs, hands and feet. So, to be able to travel and move at the speeds we want to go, we must be able to measure speed and compare different speed units.
When you look at moving objects, some appear to be moving faster or slower than others. However, suppose that you want to compare the speeds of two objects that are similar in speed or not traveling right next to each other. How can we numerically measure speed to compare the speeds of multiple objects? First, let's consider if an appropriate base unit is available to use. We use base units to measure the most basic observable properties of an object or situation. For example, base units measure properties such as length (meter, mile), mass (gram, pound) and the amount of time (hour, second) that has passed.
Unfortunately, we cannot measure speed using base units, because base units do not give us information about how fast something is traveling. Speed depends on two measurements: the distance traveled and the amount of time it takes to travel that distance. For example, a snail and a car can both travel a distance of 10 meters or for two hours, but neither measurement on its own helps you compare their speeds. What is one type of speed unit that you have probably seen when traveling in a car? (Listen to student ideas.) That's right, miles per hour (mph).
Let's look at the unit "miles per hour" more carefully. What does this mean? Let's try to figure this out using another example. Suppose I have 10 cookies to serve and two people to eat them. If you want to give each person the same number of cookies how could you figure out how many cookies each person is going to get? The answer is by dividing 10 cookies by two people and calculating that the answer is five cookies for each person. I'm sure some of you would love to be in that situation! Another way to say this is five cookies per person. The word "per" is a substitute for the words "for each." (Write the following equations on the classroom board as they are introduced.) Using mathematical symbols, we write: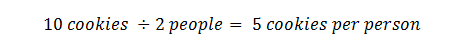
Another way to write this is in fraction form: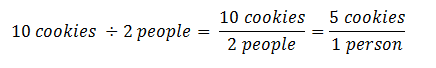
This can also be written as: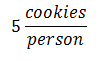
Let's go back to our speed unit, miles per hour. What have we learned the "per" stands for? In a measurement unit, "per" means rate of change, which is found using division. Miles per hour means miles traveled for each hour that passes, which is calculated using the following equation: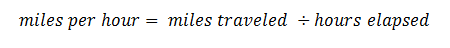
The miles traveled is the total distance covered in miles, while the hours elapsed is the total time in hours it took to cover the miles traveled. Miles per hour can be represented as a fraction.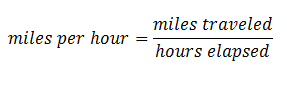
If a car travels 60 miles in two hours, then its speed is: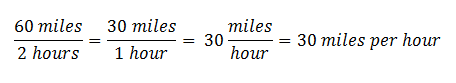
We can use this method to create different units of speed. What does the unit "mile" measure? A mile is a unit of length or distance. What type of unit is an hour? An hour is a unit of time. Thus, the general equation for speed is: 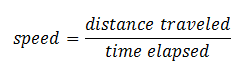
Using this equation and our miles per hour example, we can find a general equation for identifying and using units of speed: 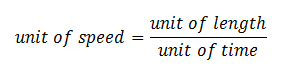
We can use any units of length and time in the equation to create a new unit of speed. The unit of speed that a scientist or engineer chooses depends on the distances and times being measured. For example, what units would engineers designing a car in the U.S. use? (miles per hour) What would engineers in Europe or Japan use? (kilometers per hour) Why? What are the differences in these units?
Let's look more closely at the unit of speed equation to see its component units. As we mentioned earlier, a unit of length or a unit of time is called a base unit. (Write the term on the board.) Base units are used to measure the most basic observable properties of objects or situations. These include length, mass and the amount of time that has passed. What are some examples of these? (As students name some examples, write them on the classroom board. Example answers: Miles, feet, yards, kilometers, meters, centimeters, hours, seconds.)
Other properties of objects or situations, such as speed, density, acceleration, power and force, are defined in terms of combinations of base units. We call these derived units. What are some possible combinations that you can think of? (Write "derived units" on the classroom board. Have students volunteer two or three different units of speed. Example answers: meters/second, cm/second, km/hour or kph, miles/hour or mph, foot per nanosecond, etc.) And in what situations might we use these examples of derived units?
In today's activity, we are going to use LEGO MINDSTORMS EV3 robots and stopwatches to measure the time it takes for a robot to travel a distance. Once we have measured time and distance, we can calculate speed.
The LEGO "speedbot" can be controlled using a touch sensor. The speedbot reports the distance it has traveled in units of centimeters (cm). You will measure the time it takes travel by using a stopwatch. Then, you will find the speedbot's speed by dividing the distance traveled by the measured time elapsed, or the time the robot traveled the full distance. Each group's robot is programmed with a different speed. By measuring the speed over multiple trials, each group will be able to determine its robot's mean speed in centimeters/second.
Procedure
Background
Whenever you use a "speed equation" and divide total distance traveled by the amount of time it took, you are calculating the mean (average) speed. For example, if you drove 100 miles in 1.5 hours, and divided distance by time, the mean (average) speed would be ~67 mph, but at any given time, you might have been traveling 80 mph or 50 mph. So, the robot might travel at a constant speed, but either way, students are still calculating its mean (average) speed by using the speed equation.
Before the Activity
- Have groups construct their robots by following the step-by-step instructions for the one-button castor bot, a basic two-motor drive robot with sturdy construction, (Figure 1) at https://www.fllcasts.com/materials/282-lego-mindstorms-castor-bot-building-instruction#is-js-viewer. This can be done during the class before the activity.

- While students are constructing the robots, program each robot's EV3 Iintelligent brick using the code in the Forward_Timing_Bot.ev3 file. Refer to Figure 2 for a screen capture of example EV3 programming code.
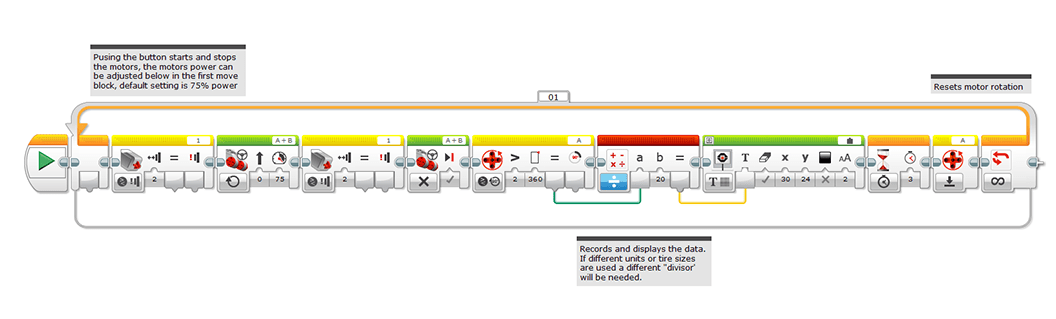
- Program each robot to start moving when a touch sensor is pressed. Then, have the robot move at a constant speed until the touch sensor is pressed a second time to stop it. So as to reduce the effect of rounding errors on the calculated speed, have the robot not respond to the touch sensor for the first 3–4 seconds.
- On its main screen, the robot displays the distance traveled in centimeters and keeps displaying this distance after it stops and until the touch sensor is pressed a second time to end the program or start again.
- Use the provided program to change the robot's set speed so students can compare the differences. Save multiple instances of the program at different motor power settings, so students can then compare the difference in speeds. The motor's power can be adjusted in the first move block to change the robot speed; the default setting is 75% power (see Figure 2 or the rbt file).
- Note: The example program generates an accurate measurement in centimeters using the wheels of the speedboat in the Figure 1 speedbot. A different robot construction or wheel size may necessitate a different conversion factor between motor rotations and centimeters, which can be measured using the wheel diameter or the number of centimeters traveled per motor rotation by the robot. Make sure to test the robots for accuracy over a one-meter distance; expect the robot to be at least 99% accurate.
- Make copies of the Pre-Activity Evaluation, Speed Equation Worksheet and Post-Activity Evaluation, one each per student.
- Make copies of the Speedbot Data Worksheet, one per group.
- Prepare to make initial role assignments in each group of two to four students: data recorder, robot timer, robot activator, note taker. For groups of three, leave off the note taker. For groups of two, have one student perform both roles of timer and recorder.
With the Students
- Administer the pre-activity evaluation and present the Introduction/Motivation content to the class.
- Explain to the class the speedbot's function and behavior, including the minimum and maximum time limits. Once students know the maximum and minimum speeds of the robot, have them compare speeds by calculating the difference.
- Divide the class into groups of two to four students each. Provide each group with a robot, stopwatch or timer, and data worksheet. Make initial role assignments in each group.
- Have groups conduct a couple of trial runs during which they observe and note the robot behavior. Expect students to observe the robot traveling in a relatively straight line for a few seconds, then stopping. If the robot does not travel perfectly straight, ask students to note possible reasons for this behavior.
- Choose two students to perform a practice run, with one controlling the robot and the other timing it. Tell students that they must stop the robot before the time limit or it will stop on its own.
- Have each group do a practice run before the experimental run.
- Remind students to rotate through the role assignments during the activity so they experience each responsibility. The group data worksheet has enough entries for each student in a group to have at least one chance to control the robot. Direct the data recorder for each trial to write down the data for that trial into the appropriate worksheet row as well as his or her name and the timer's name.
- Conclude by having students individually complete the speed equation worksheets and post-activity evaluations, as described in the Assessment section.
Vocabulary/Definitions
base unit: A unit used to measure fundamental properties such as length and time. Examples: Miles, kilometers, yards, feet, meters, seconds, hours.
derived unit: A unit used to measure properties such as speed or volume. Composed of a combination of base units, such as miles per hour.
distance: The length between the starting and stopping point of a moving object.
time elapsed: The amount of time that passes between an object starting and stopping.
Assessment
Pre-Activity Assessment
Knowledge Survey: Administer the Pre-Activity Evaluation to gauge students' understanding and opinions about of units, speed and robots. Have students list any units they know, such as for length, time, weight, speed. See if they know the equation (and base units) for determining speed before giving it to them.
Activity Embedded Assessment
Observations: During the activity, observe groups' cooperation skills, how well they share, and how efficiently they complete the tasks. Have students rotate through the different roles and take on different responsibilities. Have all students calculate the speeds and compare answers within their own teams. If their answers vary, have students work together to determine the correct solutions.
Post-Activity Assessment
Data Crunching: Once students have collected the data on the Speedbot Data Worksheet, review with them how to do long division. Depending on their division skill levels and the stopwatch accuracy, students may need to round the results before dividing. As necessary, review rounding with them. Round the time measurement to the nearest second; round the distance and speed to the tenths or hundredths place. If students do not know how to do long division with a decimal dividend, review it with them or round to the nearest centimeter and use fractional remainders. Have students individually complete the Speed Equation Worksheet with their groups' data, either in class or for homework. Have students use calculators to verify their work.
Post-Eval: Administer the Post-Activity Evaluation. Review students' answers to assess their depth of comprehension of the activity concepts.
Investigating Questions
- What is the most accurate way to measure the speedbot's speed? (Answer: For each trial, let the robot move until it times out. That way, the time is always known to be exactly 15 seconds, or whatever timeout period the teacher selects.)
- Why doesn't the robot travel in a perfectly straight line? (Answer: The robot might not travel in a perfectly straight line for many reasons, such as different amounts of friction between the left and right sides of the robot, the left and right motors might produce slightly different power amounts, etc.)
- Whose robot was the fastest? And how do we know this?
- Whose robot went the farthest/shortest and whose took the longest?
- In everyday life, how does speed affect your life?
- What are some of the positives and negative aspects of a high rate of speed?
- How can we design the robot to go faster? What tools could we use? (Answers will vary, but this is an important question to explore students' engineering design ideas.)
Activity Extensions
Once each group has determined a mean value, have the class make a plot of robot speed vs. motor power.
Have students take the maximum distance that the robot traveled and program the robot to travel that distance. Then have students compare the two sets of data.
Activity Scaling
- For younger students, end the activity after they find the speed for each trial. Let students who are developing division skills use calculators, after attempting to perform division by hand.
- For older/more advanced students, have groups use the exact distance values displayed by the EV3 to find the mean speeds of their speedbots. Have students who are familiar with long division start the speed equation worksheet during the activity.
Additional Multimedia Support
Show students a robotic speed challenge in which micromouse robots navigate a maze in the shortest amount of time (3:43-minute video): http://www.youtube.com/watch?v=76blllun09Q.
Show students a video of a high-speed robot hand to illustrate the importance of speed for robotics because a limiting factor for the success of robotic limbs is the speed that the various prosthetics move (2:59-minute video): http://www.youtube.com/watch?v=-KxjVlaLBmk.
Show students speed comparisons for a road car vs. race car vs. Formula 1 car (7:28-minute video): http://www.youtube.com/watch?v=awtqcTVgmpo.
Show students this inspiring LEGO robotic arm video to get them interested in how LEGO robotics can be used (3:22-minute video): http://www.youtube.com/watch?v=KR3IiXvzrds.
A great resource for LEGO robotics ideas and designs: http://ev3lessons.com/.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Expanding on the topic of objects in motion covering Newton's laws of motion, acceleration and velocity, which are taught starting in third grade, students are introduced to new concepts of speed, density, level of service (LOS) (quality of roadways), delay and congestion.

Students learn that navigational techniques change when people travel to different places — land, sea, air and space. For example, an explorer traveling by land uses different navigation methods and tools than a sailor or an astronaut.

Students are introduced to the concepts of force, inertia and Newton's first law of motion: objects at rest stay at rest and objects in motion stay in motion unless acted upon by an unbalanced force. Students learn the difference between speed, velocity and acceleration, and come to see that the cha...
Copyright
© 2013 by Regents of the University of Colorado; original © 2011 Polytechnic Institute of New York UniversityContributors
Sam Sangankar, James CoxSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: October 16, 2020








User Comments & Tips