Quick Look
Grade Level: 12 (9-12)
Time Required: 4 hours
(can be split into different days)
Expendable Cost/Group: US $1.00 This activity requires use of non-expendable (reusable) LEGO MINDSTORMS EV3 core set, sensor and software; see the Materials List for details.
Group Size: 3
Activity Dependency: None
Subject Areas: Algebra, Data Analysis and Probability, Measurement, Number and Operations, Physics, Science and Technology
NGSS Performance Expectations:

| HS-ETS1-2 |
| HS-PS2-1 |
| HS-PS3-3 |

Summary
Students design, build and evaluate a spring-powered mouse trap racer using the engineering design process. For evaluation, teams equip their racers with an intelligent brick from a LEGO© MINDSTORMS© EV3 Education Core Set and a HiTechnic© acceleration sensor. They use acceleration data collected during the launch to compute velocity and displacement vs. time graphs. In the process, students learn about the importance of fitting mathematical models to measurements of physical quantities, reinforce their knowledge of Newtonian mechanics, deal with design compromises, learn about data acquisition and logging, and carry out collaborative assessment of results from all participating teams.Engineering Connection
Automotive engineering is a branch of engineering concerned with all aspects of automobile development. Automotive engineers design and build vehicles to meet desired specifications and cost constraints. Specifications may include light weight, high engine power rating, large acceleration and top speed, high fuel efficiency, exceptional safety characteristics, and low cost – goals that may not ALL be achievable at the same time. Careful design trade-offs must usually be made. As part of the engineering design process, safety tests are often performed, such as tests in which vehicle prototypes collide with a target in a controlled fashion. Acceleration sensors aboard the vehicle measure the magnitude of impact forces. A safe vehicle effectively dampens the force of impact, as evidenced by low accelerometer readings, so passengers in real accidents are not subjected to excessive and dangerous forces.
Learning Objectives
After this activity, students should be able to:
- Compute and plot velocity and displacement graphs from given acceleration data on the same time interval.
- Explain the importance of fitting simple (linear) models to measurements.
- Predict the performance of a mouse trap racer given its characteristics.
- Explain sensor-based data acquisition/logging, and basic data analysis using a spreadsheet.
- Explain the steps of the engineering design process.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-ETS1-2. Design a solution to a complex real-world problem by breaking it down into smaller, more manageable problems that can be solved through engineering. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Design a solution to a complex real-world problem, based on scientific knowledge, student-generated sources of evidence, prioritized criteria, and tradeoff considerations. Alignment agreement: | Criteria may need to be broken down into simpler ones that can be approached systematically, and decisions about the priority of certain criteria over others (trade-offs) may be needed. Alignment agreement: | |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS2-1. Analyze data to support the claim that Newton's second law of motion describes the mathematical relationship among the net force on a macroscopic object, its mass, and its acceleration. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Analyze data using tools, technologies, and/or models (e.g., computational, mathematical) in order to make valid and reliable scientific claims or determine an optimal design solution. Alignment agreement: Theories and laws provide explanations in science.Alignment agreement: Laws are statements or descriptions of the relationships among observable phenomena.Alignment agreement: | Newton's second law accurately predicts changes in the motion of macroscopic objects. Alignment agreement: Attraction and repulsion between electric charges at the atomic scale explain the structure, properties, and transformations of matter, as well as the contact forces between material objects.Alignment agreement: | Empirical evidence is required to differentiate between cause and correlation and make claims about specific causes and effects. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS3-3. Design, build, and refine a device that works within given constraints to convert one form of energy into another form of energy. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Design, evaluate, and/or refine a solution to a complex real-world problem, based on scientific knowledge, student-generated sources of evidence, prioritized criteria, and tradeoff considerations. Alignment agreement: | At the macroscopic scale, energy manifests itself in multiple ways, such as in motion, sound, light, and thermal energy. Alignment agreement: Although energy cannot be destroyed, it can be converted to less useful forms—for example, to thermal energy in the surrounding environment.Alignment agreement: Criteria and constraints also include satisfying any requirements set by society, such as taking issues of risk mitigation into account, and they should be quantified to the extent possible and stated in such a way that one can tell if a given design meets them.Alignment agreement: | Energy cannot be created or destroyed—it only moves between one place and another place, between objects and/or fields, or between systems. Alignment agreement: Modern civilization depends on major technological systems. Engineers continuously modify these technological systems by applying scientific knowledge and engineering design practices to increase benefits while decreasing costs and risks.Alignment agreement: |
Common Core State Standards - Math
-
Look for and make use of structure.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Model with mathematics.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on a single count or measurement variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on two categorical and quantitative variables
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Calculate expected values and use them to solve problems
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve equations and inequalities in one variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the attributes of design.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of engineering design.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Cite examples of the criteria and constraints of a product or system and how they affect the final design.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Optimize a design by addressing desired qualities within criteria and constraints.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
Look for and make use of structure.
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
-
Model with mathematics.
(Grades
Pre-K -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on a single count or measurement variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Calculate expected values and use them to solve problems
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve equations and inequalities in one variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on two categorical and quantitative variables
(Grades
9 -
12)
More Details
Do you agree with this alignment?
New York - Science
-
Design a solution to a complex real-world problem by breaking it down into smaller, more manageable problems that can be solved through engineering.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Analyze data to support the claim that Newton's Second Law of Motion describes the mathematical relationship among the net force on a macroscopic object, its mass, and its acceleration.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Design, build, and refine a device that works within given constraints to convert one form of energy into another form of energy.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- LEGO MINDSTORMS EV3 robot, such as EV3 Core Set (5003400) at https://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3
- LEGO MINDSTORMS Education EV3 Software 1.2.1, free online, you have to register a LEGO account first; at https://www.lego.com/en-us/mindstorms/downloads/download-software
- computer, loaded with EV3 1.2.1 software
- HiTechnic Software Downloads at https://www.hitechnic.com/downloadnew.php?category=38
- mouse trap with trigger pin removed
Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:
- LEGO MINDSTORMS NXT robot, such as the NXT Base Set
- computer, loaded with NXT 2.1 software
- 1 HiTechnic NXT Acceleration/Tilt sensor
- laptop or desktop computer with imported HiTechnic Acceleration Sensor Block for MINDSTORMS NXT Software Versions 2.0
To share with the entire class:
- different diameter LEGO wheels and miscellaneous LEGO pieces (provided in the LEGO MINDSTORMS EV3 Education Core Set)
- string (nylon, kelvar or equivalent)
- roll of 1-2 inch packaging tape
- meter stick
- kitchen scale
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_mouse_trap_activity1] to print or download.Pre-Req Knowledge
Students should have knowledge of the following topics: kinematic equations, Newton's second law, Hooke's law, basic rotational dynamics, sample mean and variance (optional), functions of time (that is, acceleration, velocity and displacement). It is helpful to have some experience with LEGO robots.
Introduction/Motivation
(In advance, create a mousetrap racer to demonstrate to the class, and have available a ball, inclined beam, threaded buttons and eraser.)
The invention of the wheel and use of wheeled vehicles since 3500 BC brought about tremendous progress. Goods and people were transported much faster than was possible before, energizing commerce, strengthening military capabilities, increasing food supplies, and helping many laborers to become artisans and scholars. Wheeled vehicles were mostly driven by horses until the late 1700s, when steam engine vehicle prototypes were created, and 1880s, when the first automobiles based on the internal combustion engine were built.
The basic principle behind a self-powered vehicle is to convert some form of potential energy into motion, or kinetic energy. There are many forms of potential energy, for example gravitational potential energy associated with an object at a certain distance from earth, elastic potential energy stored in a deformed spring, potential energy in a charged capacitor or current-carrying inductor, chemical potential energy in gasoline or battery, and others. The simplest vehicle can be built without any engine at all! How? (Illustrate by using gravitational potential energy – let a ball roll down an inclined surface.) Of course, a vehicle is truly useful when it can move by itself on a level surface, or even up along a hill. This requires internal means of propulsion.
In today's activity, groups will build and evaluate mouse trap racers using the engineering design process. The elastic potential energy in a set mouse trap is the means of propulsion. (Show students Figure 1.) A typical racer consists of a cart taped to a mouse trap. A piece of string is attached to the swinging trap bracket. In operation, this string is wound around the driving axle (in this case, the rear axle), which also sets the trap. The driving wheels are held tightly until the launch. Usually, it is best to remove the trigger pin and hold on to the driving wheels, since this makes for a well-controlled and repeatable launch. Let's see an example. (Demonstrate using a racer built in advance.)
What performance criteria can we use to evaluate a racer design? Let's first predict typical racer behavior. We can expect that during the launch, the racer will accelerate for as long as the string exerts a torque on the driving axle. The maximum velocity will be achieved just at the point when all of the string has unwound. This occurs when the mouse trap has shut closed. The racer will then gradually come to a stop as friction forces act to oppose its forward motion. Therefore, one way to quantify the racer performance is by means of a table of values for the following quantities:
- top acceleration
- top deceleration
- top velocity
- total distance traveled
Ideally, we would like the largest possible values for all these quantities, except top deceleration, which we would like to be as close to zero as possible. In other words, we would like to minimize friction forces. Since we will have access only to acceleration measurements, we will need to compute velocity and distance traveled from the measured acceleration versus time graph.
Let's now summarize some factors that affect mouse trap racer performance.
- Mass – by Newton's second law (F = m x a, where F = applied force, m = mass and a = acceleration), for the same applied force, heavier masses will experience less acceleration. Make your design lightweight!
- Driving wheel diameter and moment of inertia – for the same rotation, wheels of larger diameter will cover a greater linear distance (illustrate using circumference arguments), and for the same diameter and applied torque, wheels with larger moment of inertia will undergo less linear acceleration (illustrate using the spinning buttons demo, as in the Figure 2: while spinning the buttons in front of the class, it should be obvious that the larger button does not spin around the strings as fast as the smaller button).

Figure 2. These threaded buttons have different moments of inertia. See video demonstration in the References section. - Driving wheel traction – rubber tires provide better traction than plastic tires, and for the same tire material, larger surface contact results in better traction (perform the eraser demo, as in the Figure 3, which shows that greater surface contact creates more traction require more force to move the eraser). Use tires!

Figure 3. An eraser is easier to push when lying on its narrow side. It is harder to push an eraser lying on its broad side. - Time duration over which torque is applied to the driving wheels – same torque applied for longer results in larger velocity and greater distance traveled.
- Magnitude of the applied torque – for the same moment of inertia and wheel diameter, larger applied torque results in larger linear acceleration.
- Friction forces between the axles and racer body – smaller friction forces result in less deceleration and therefore greater distance traveled. Make sure your axles rotate freely!
Is it possible to design a racer with the best possible values for all four parameters? Are there any compromises your team has to make? Once in your teams, begin by diving into steps 1 and two of the engineering design process: ask to identify needs and constraints and researching the problem for this activity.
Procedure
Before the Activity
- Gather and prepare demonstration materials (ball, inclined beam, mouse trap racer, threaded buttons, eraser).
- Gather and prepare activity materials. Make sure each computer has a copy of the Data Analysis Spreadsheet and the EV3 MINDSTORMS program.
- Make copies of the Statistics Worksheet and Analysis Worksheet (one per student).
With the Students
- Divide the class into groups of three students each.
- Hand out the worksheets and review the information, equations and questions as a class. Make sure each student knows what they need to do during the activity, as well as during the analysis.
- In groups, have students go into step 3, 4, and 5 of the engineering design process: imagine, plan, and create their mouse trap racers. It is a good idea to conduct this activity with moderately experienced students (LEGO novices take more time to construct the racers). Have groups develop as many different designs as possible in order to make the collaborative assessment a success – encourage creativity! Provide the following general guidelines.
- Use tape sparingly to hold the mouse trap in place. Show that tape is only needed on the bait side of the mouse trap. As students why. (Answer: This is an example of an "efficient engineering solution." Why use more than is needed? Often students use tape liberally over the entire mouse trap even though it is unnecessary in order to secure the trap in place.)
- Place the EV3 brick away from the metal trap bracket.
- Important: Mount the acceleration sensor as parallel to the ground as possible, and with the x-axis pointing in the direction of motion. Tilting the accelerometer with respect to the ground results in erroneous measurements.

Worm gears can hold a wrapped string tightly in place. 
One way to mount the EV3 brick. 
Mount your accelerometer with the x-axis pointing in the direction of motion, parallel with the floor.
- Have students open the EV3 program mousetrap.ev3, which is shown in Figure 4. Explain the algorithm. The program essentially waits for appreciable accelerometer readings, then starts logging time and acceleration readings in files time.txt and acceleration.txt located on the EV3 brick. Each repetition of the experiment appends (does not delete) data collected from previous trials. One hundred data values are collected for each trial. Data from each trial is separated by a space. Have students consult help menus, and provide extra assistance where needed. (Note: Depending on teaching objectives, provide more details; for example, by discussing each block in the program, exploring how variables are passed from block to block, etc. This could be added for advanced students; it is not necessary for lower grades for whom the algorithm explanation above is sufficient.)
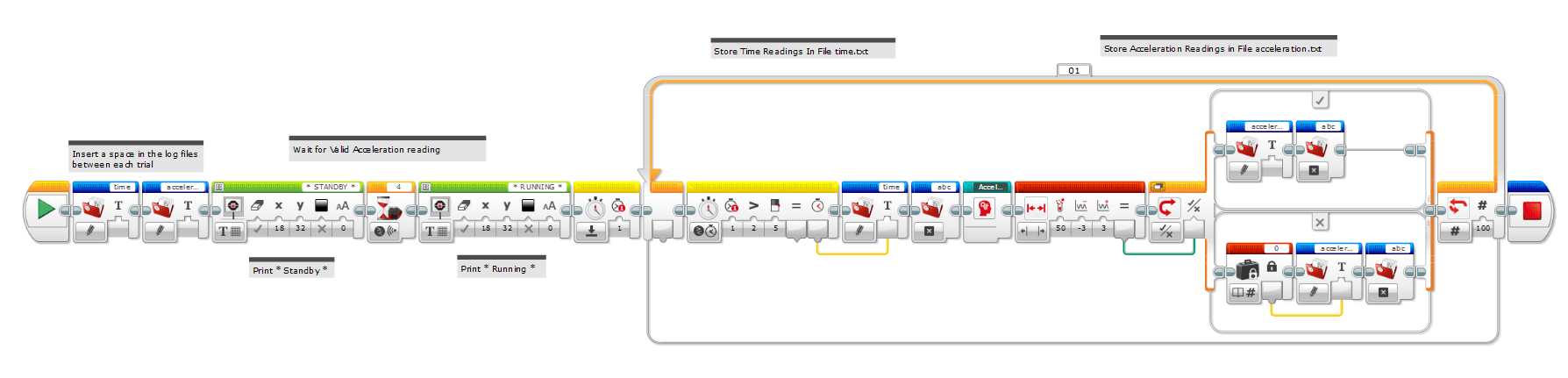
Figure 4. This program is used to collect acceleration measurements with corresponding time values. - Connect the EV3 brick to the computer using the programming cable in the LEGO MINDSTORMS Education EV3 Core Set. Go to the EV3 window by pressing the orange button in the lower right hand corner in Figure 4. In the window, under the Communications tab, verify that the EV3 is connected. Click on the Memory tab. Notice how much memory is taken up by programs and data (if any). Click Delete All. Notice how much more memory is now available. The panel labeled EV3 Data lists some useful information, such as your battery status (recharge the battery if needed). Now click Close.
- Download the program mousetrap.ev3 to the EV3 brick by clicking on the Download button in the lower right hand corner in Figure 4 (hold your mouse pointer over each button to read its function). Now go to the EV3 window again, and verify that your program has downloaded successfully. Now click Close, and disconnect the programming cable. You are now ready to run the mouse trap racer and log data!
- Wind the string around the driving axle, thereby setting the mouse trap. Set the racer up against a wall, holding on to the wheels. Find the program mousetrap on your brick, and be ready to run it the moment after the launch. When ready, launch your racer (see sample launch video in references). Make sure both racer and program fully stop before proceeding.
- Go to the EV3 window and under Memory tab, verify that log files time.txt and acceleration.txt have been created (these should be under the heading Other). Select the file time.txt and click Upload. Choose the Desktop folder and click OK. The log file with time values should now be located on your desktop. Repeat the procedure to upload the file acceleration.txt. Notice that if these files are already on your desktop, overwrite them with those you have generated.
- Open the spreadsheet Analysis Spreadsheet. Go to the sheet labeled Raw Data (click on the tab in the lower left hand corner of the screen). Notice how sample data has been filled in the time (ms) and Trial 1 columns. Go to the Desktop, and open the file time.txt in Notepad. Highlight and copy the time data. In Excel, select (click on) cell A3, and paste your time values. Now scroll down to make sure you have not entered any values beyond the cell A102. Repeat the procedure with the data in file acceleration.txt.
- Now go to the sheet Analysis. You will need to type in values in the cells highlighted in red. Cell H3 is the time value at which your racer achieves its highest velocity. Eyeball the acceleration data and roughly note the point at which acceleration values max out. Type in the corresponding time value in cell H3. Cell H4 is the time value at which your racer comes to a stop. Eyeball the acceleration data, and roughly note the point at which acceleration values become very small and mostly constant (ideally zero). Enter the corresponding time value in cell H4.
- Now look at the plots in the sheet Graphs. Notice how noisy the measured acceleration values are (look at the graphs in the first column). Does your velocity graph reflect reality? What about the displacement graph? Look at the second column, where we fit a model using two constants in the time intervals 0 to t1 and t1 to t2. Try to answer the same questions. Repeat with the third column, where we use a model of two line segments over the same time intervals to model the racer acceleration profile.
- Now gather data for nine more trials. That is, repeat the launch procedure to obtain acceleration data for ten trials. You don't need to upload the data to Excel every time, since the log files will be appended (not overwritten) with new data each time you run the program mousetrap. After you are done, upload your log files to Desktop as before (see sample attached log files). Copy and paste acceleration data from file acceleration.txt in columns C3 through K3. Time values do not change, so time data needs to be entered only once. Type in new values for t1 and t2 in the cells highlighted in red, but use the average of raw readings (column B in the Analysis sheet) to estimate these times.
- Analysis: The sheet Analysis does several things.
- Column D contains acceleration readings in the proper units (m/sec2). In column E and F, we compute velocity and displacement. Refer to the Analysis Worksheet for formulas.
- In columns H through O, we fit a model that assumes constant acceleration over the two time intervals 0 to t1 and t1 to t2 (Model 1 – piecewise constant model). We use a procedure called constrained least squares, details of which are optional, but are given in the attachment Derivations.
- In columns Q through EH, we use constrained least squares to fit two lines over the time intervals 0 to t1 and t1 to t2 (Model 2 – piecewise linear model).
- Go to the sheet labeled To Submit, and type data into cells highlighted in red. Weigh your racer, and enter the mass in grams. Measure the driving wheel diameter, and length of string wrapping around the driving axle, and enter those values. Submit this table to your teacher.
Vocabulary/Definitions
acceleration: Change in velocity at two time instants, divided by the time interval. In this activity, "acceleration" will be used only for positive changes in velocity.
accelerometer: A sensor used to measure acceleration.
algorithm: A sequence of logical steps that achieve a given objective, and are intended to be programmed into a computer.
data acquisition: Usually, a process in which measurements are made under computer control.
data logging: A process of storing measurements in a computer file.
deceleration: Negative change in velocity at two time instants, divided by the time interval.
displacement: Distance travelled between two time instants.
kinetic energy: Energy associated with a system with nonzero velocity.
moment of inertia: A measure an object's ability to resist rotation.
potential energy: Energy in a system that can be used to perform work.
torque: A measure for the tendency of an object to rotate about an axis when subjected to a force.
velocity: Displacement between two time instants, divided by the time interval.
Assessment
Pre-Activity Assessment
Sharing Experiences: Lead a class discussion about student experiences with cars. Who likes sporty sedans? What about fuel efficient/hybrid vehicles? Bikes?
Activity Embedded Assessment
Worksheets: Complete the Analysis Worksheet and Statistics Worksheet. The Statistics Worksheet explains why several runs are conducted during the experiment instead of just one. The Analysis Worksheet explains what is done to convert acceleration to velocity, and then to displacement, without calculus. It does not matter which is completed first, and alternatively, assign the worksheets as homework.
Post-Activity Assessment
Collaborative assessment of group results: Lead a collaborative effort to make sense of the activity. Discuss what worked and what didn't. Each group built a unique racer, and should have obtained different insights into how physics laws applied to their designs. Discuss which racer scored better in each of the four metrics (top acceleration, top deceleration, top velocity, total distance travelled), and why (a tab on the Data Analysis Spreadsheet should help). Ask students if any one design outperformed in all categories, or did students find different designs excelled in only one or two categories? Discuss how concepts of engineering design trade-offs apply. Ask students to suppose they were challenged to repeat the activity, but with actual application requirements. How would the insights they gained be used to craft a racer to satisfy the unique application requirements they were provided? Try to include every student in this discussion to get as many possible ideas and insights as possible shared with the class.
Investigating Questions
Collect the To Submit data from all teams, and make plots of performance metrics vs. racer weight, wheel diameter and string length. Lead a collaborative class discussion. Ask the students:
- How is the top acceleration related to the mass and wheel diameter of the mouse trap racer?
(Answer: In general, a racer with a smaller mass and larger diameter wheels has a larger top acceleration. This may not be true if the wheels have an especially large moments of inertia and/or bad traction. The wheel mass (and particularly mass distribution) is therefore another important factor to consider.)
- How is the top velocity related to the racer mass and wheel diameter?
(Answer: The lighter racer, with larger diameter wheels, often achieves the best top velocity, unless, as in the previous answer, the wheels have large moments of inertia and/or poor traction.)
- How is the total displacement related to the wheel diameter and string length?
(Answer: Wheels with larger diameter travel a longer linear distance, and of course, the longer the wheels experience torque from the wound string, the further the racer travels.)
Compare and discuss individual team results.
- Do plots in the first column in sheet Plots reflect reality? For example, does your computed velocity ever become negative? Does your total displacement ever decrease? If yes, why do you think this is so?
(Answer: This question asks students to make the "data vs. reality" connection, and realize that some of the plots make no sense based on observations of the racer motion. For example, the racer comes to a complete stop (zero final velocity), and always travels forward (no decrease in displacement), and any deviations from this in the data should be due to shortcomings in their data analysis techniques.)
- Do plots in the second column (Model 1) in sheet Plots reflect reality? For example, can we really assume constant acceleration over time interval 0 to t1, given that the torque applied to the axle by the mouse trap bracket is proportional to the bracket angle (Hooke's law)? Nevertheless, is this a reasonable approximation? Compare the maximum displacement value with the actual measured distance your racer travels.
(Answer: The constant acceleration model is not accurate, since it does not account for Hooke's law, but it is much simpler than the linear model. Have students look at the linear model and see if the slopes of the segments are small enough to be approximated with constants. What is meant by "small enough" is a great subject for a class discussion.)
- Repeat for plots in the third column (Model 2). How does this model compare to Model 1? Is Model 2 more accurate? If yes, why do you think so? Explain using physics arguments.
(Answer: Model 2 is more accurate, since it attempts to account for the fact that the torque exerted on the trap bracket is proportional to the bracket angle. Curious students may wish to derive the exact behavior of the trap, which is beyond the scope of this activity.)
Safety Issues
Warn students to exercise caution when setting the mouse trap. Keep fingers away from the bait area and sharp or rough edges.
Troubleshooting Tips
- Students may encounter the problem in which, instead of numbers, their log files contain the character ÿ. If this happens, have them manually delete such characters using Notepad. Correctly formatted log files should look like the attached files sample_time.txt and sample_acceleration.txt.
- Sometimes, the EV3 may omit a carriage return after one or more entries. Have students manually correct this problem in Notepad before copying data into Excel.
- In case of corrupted or incorrectly gathered data, have students delete their log files from the EV3 memory window, and rerun the experiment.
Activity Scaling
- For lower grades, adapt and modify the worksheets, as needed.
- Have calculus physics students compute velocity and displacement from acceleration data using trapezoid and other integration rules.
Additional Multimedia Support
Inertia spinning button. (39 seconds) Accessed December 20, 2012. http://www.youtube.com/watch?v=Gt_c4Tji8_s
How to Build a Mousetrap Car, Part 1 of 5. (10 minutes) Accessed December 20, 2012. http://www.youtube.com/watch?v=3SbbZsx-qwo
Simple Mouse Trap Car Goes 138 Feet (example launch - the ultimate mouse trap car with LP records for wheels; 4 minutes) Accessed December 20, 2012. http://www.youtube.com/watch?v=XZ23q0QXPx0
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...
Copyright
© 2013 by Regents of the University of Colorado; original © 2009 Polytechnic Institute of New York UniversityContributors
Pavel KhazronSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: October 16, 2020






User Comments & Tips