Quick Look
Grade Level: 11 (11-12)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00 This activity requires the use of non-expendable (and reusable) LEGO® MINDSTORMS® kits with sensors and other supplies, estimated at $438; see the Materials List for details.
Group Size: 4
Activity Dependency: None
Subject Areas: Physics
NGSS Performance Expectations:

| HS-PS3-1 |
Summary
Students are introduced to the concept of projectile motion, of which they are often familiar from life experiences, such as playing sports like basketball and baseball, even though they may not understand the physics involved. Students use tabletop-sized robots to build projectile throwers and measure motion using sensors. They compute distances and velocities using simple kinematic equations and confirm their results through measurements by hand. To apply the concept, students calculate the necessary speed of an object to reach a certain distance in a hypothetical scenario: A group of hikers stranded at the bottom of a cliff need food, but rescuers cannot deliver it themselves, so they must devise a way to get the food to the hikers. A student worksheet is provided.
Engineering Connection
Understanding projectile motion is important to many engineering designs. Any engineered design that includes a projectile, an object in motion close to the Earth's surface subject to gravitational acceleration, requires an understanding of the physics involved in projectile motion. This includes machines such as motocross bikes made for launching off jumps to weapons such as missiles, turrets and high-powered cannons. NASA engineers apply projectile motion concepts as they predict the paths of meteorites that may enter the Earth's atmosphere or disrupt satellite transmissions. The combination of a physical understanding of projectile motion and the mathematical ability to solve equations enables engineers (as well as young students) to predict projectile trajectories.
Learning Objectives
After this activity, students should be able to:
- Describe the trajectory of an object in projectile motion.
- Determine how far an object will travel based on initial conditions.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS3-1. Create a computational model to calculate the change in the energy of one component in a system when the change in energy of the other component(s) and energy flows in and out of the system are known. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Create a computational model or simulation of a phenomenon, designed device, process, or system. Alignment agreement: | Energy is a quantitative property of a system that depends on the motion and interactions of matter and radiation within that system. That there is a single quantity called energy is due to the fact that a system's total energy is conserved, even as, within the system, energy is continually transferred from one object to another and between its various possible forms. Alignment agreement: Conservation of energy means that the total change of energy in any system is always equal to the total energy transferred into or out of the system.Alignment agreement: Energy cannot be created or destroyed, but it can be transported from one place to another and transferred between systems.Alignment agreement: Mathematical expressions, which quantify how the stored energy in a system depends on its configuration (e.g. relative positions of charged particles, compression of a spring) and how kinetic energy depends on mass and speed, allow the concept of conservation of energy to be used to predict and describe system behavior.Alignment agreement: The availability of energy limits what can occur in any system.Alignment agreement: | Models can be used to predict the behavior of a system, but these predictions have limited precision and reliability due to the assumptions and approximations inherent in models. Alignment agreement: Science assumes the universe is a vast single system in which basic laws are consistent.Alignment agreement: |
Common Core State Standards - Math
-
Reason quantitatively and use units to solve problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop an understanding of the characteristics and scope of technology.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Students will develop abilities to use and maintain technological products and systems.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
Reason quantitatively and use units to solve problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
New York - Science
-
Create a computational model to calculate the change in the energy of one component in a system when the change in energy of the other component(s) and energy flows in and out of the system are known.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
To share with the entire class:
- 1 LEGO MINDSTORMS kit to build a ball launcher (suggestion: LEGO MINDSTORMS EV3 Education Core Set available athttps://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3)
- LEGO Education Large Tires and Hubs, available at https://www.brickowl.com/catalog/lego-parts/vehicle/tire-tread
- Ping pong ball or balls to launch (such as plastic balls included in LEGO MINDSTORMS kit)
- measuring tape
- colored masking tape, with which to mark a circle target
- stopwatch
- Projectile Motion Problem Worksheet, one per student
Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:
- LEGO MINDSTORMS NXT Base Set
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_projectile_activity1] to print or download.Pre-Req Knowledge
A basic understanding of distance, time, velocity and acceleration. Ability to calculate the average velocity of an object traveling a certain distance over a period of time. Familiarity with acceleration due to gravity.
Introduction/Motivation
Have you ever wondered how far a ball can travel when you throw it? Or better yet, how hard you need to hit a baseball to get a home run? These are real questions that not only apply to baseball, but other real-life situations including the paths of meteorites and trajectories of rockets.
In today's activity, we will create a ball launcher that shoots balls in the direction of our choosing. Using simple math representing the forces that act on a ball, we can predict how far it will travel in the air. We can even calculate its location at a given time.
Why is this important? Let's imagine that while hiking with friends, some of them end up stranded at the bottom of a cliff. We don't have the equipment to reach them or rescue them, and so we must call for help. We're informed that rescuers will be able to come save our friends in the morning, but in the meantime, our friends are starving. It is our goal to construct a device that can shoot food down to them. By studying the motion of things traveling in the air, also known as projectiles, we can figure out just how fast the food needs to be launched in order for it to get to them. Be careful! If we shoot too low, the food will be destroyed and if we shoot too high, we may attract unwanted creatures such as bears.
The motion of a projectile, a container of food in this case, traveling through the air is called projectile motion. We see projectile motion in action almost every day. Can you think of any examples in which you have seen projectile motion?
Procedure
Background

To effectively deliver this activity, it is recommended that the teacher be familiar with LEGO MINDSTORMS robots. Otherwise, use another means of launching a ball, such as a rubber band or a small catapult.
It is also necessary for the instructor to be familiar with kinematics and equations of motion (see below) and understand the kind of forces that act upon an object in projectile motion. For this activity, we only use gravity acting on the food in the vertical direction, and we assume that the horizontal direction does not experience any forces (air resistance is neglected). For example, if a ball is dropped from a height of 4 meters, similar to what is about to happen in Figure 1, how long does it take to reach the ground? This requires using Equation 2 (see below) and making the initial distance equal to 4 meters and the final distance equal to 0. The initial velocity is taken as zero because the object was dropped, and the acceleration downward is equal to the gravitational acceleration, = -9.81 m/s. Solving Equation 2 for t gives you 0.9 seconds.
Note: The equations listed below are considered the fundamental equations of motion. The combination of these four equations can solve any projectile motion problem, given the correct number of initial conditions. Multiple conditions can exist, so plugging in where a ball starts or how fast it starts resolves all other unknowns.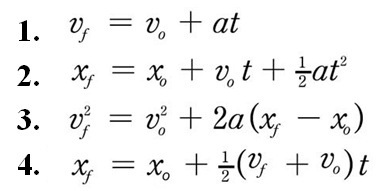
In addition to the kinematic equations for projectile motion, the instructor should review the concepts of kinetic and potential energy with students in the context of this activity. While in the air, a projectile's total energy is the sum of its kinetic energy (energy of motion) and its potential energy (stored energy; in this case, due to gravity and the position of the projectile above the ground). Equations for calculating kinetic and potential energy of a projectile are shown below.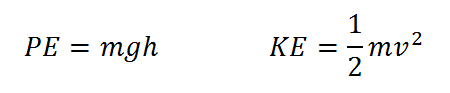
Before the Activity
- Gather materials and make copies of the Projectile Motion Problem Worksheet.
- Prepare LEGO parts and make sure all the pieces required for constructing the launcher are available.
- Construct a launcher before class using the LEGO Digital Designer (LDD) ball launcher instructions at: https://www.teachengineering.org/lego/building_instructions_projectile/building_instructions.html
- Prepare a MINDSTORMS code to initiate motor power. A simple sample code is as follows:
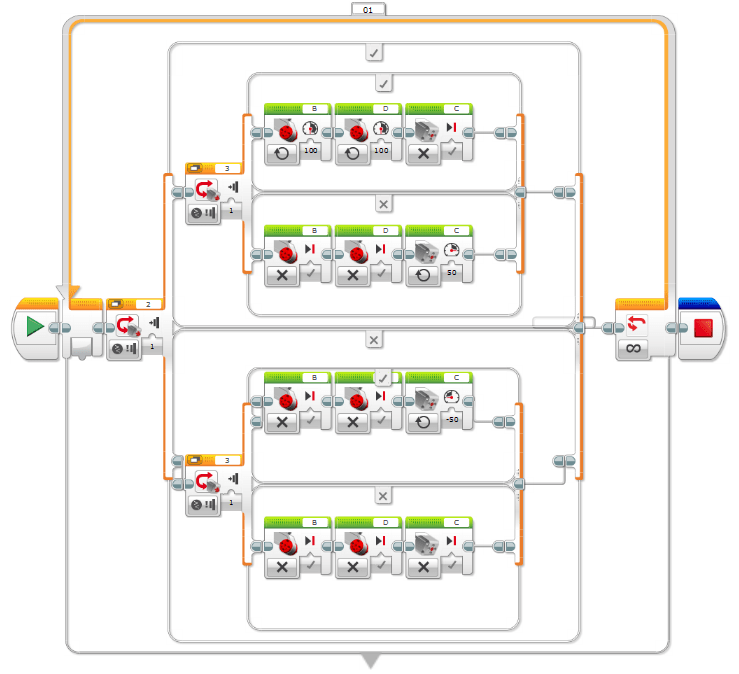
The MINDSTORMS code above uses two pushbuttons to pitch the cannon up and down and to spool up the two ball-pitching motors. Pressing one switch (switch 2) pitches the cannon up, and pressing the other switch (switch 3) pitches the cannon down. Pressing both buttons simultaneously will start the ball-pitching wheels spinning. Adjust power, and conversely, speed at which the ball is launched by just changing the motor power values between 0-100.
Note: Do not over-actuate the pitch legs, as the structure will block their rotation, breaking the gearing system.
With the Students
- Describe projectile motion in laymen's terms, much like in the Background section. Describe the path an object traverses in the air. Ask why the path appears the way it does. Explain the terms in Equations 1-4 and go through an example with students (such as the one provided in the background section). Point out that Equations 2 and 3 have a squared term. In general, this means that the changes in velocity and distance as the ball moves are not linear, much like the motion of the ball as it moves in air.
- Ask students where they have seen examples of projectile motion. Ask why we might want to study it. Write down student ideas on the classroom board for all to see.
- Describe the real-world importance to students, such as predicting the path or landing of meteors, accuracy in aiming a ball or rocket, or delivering food to hikers. (Refer to the Engineering Connection section for a few more examples.)
- Hand out the worksheet with problems, each solving for a different kind of variable, such as time, initial velocity or distance. (Worksheet answers and solutions are provided on the Projectile Motion Problem Worksheet Answer Key. Review answers with students, ensuring that students can explain why they used certain equations and can explain step by step how to use the equations to solve each problem.
- Build a ball shooter using LEGO and EV3 motors. See Figure 2 for an example, although the shooter can be constructed in more than one way.

Figure 2. Example ball shooter robot. - Place the launcher on a desk a few feet above the ground. Identify the area to hit as a couple of feet from the base below. Mark the designated target as a circle made of tape.
- Let students observe the ball launcher setup. Have them measure the vertical distance between the ball release point on the machine and the ground. Then have them shoot balls at a designated spot and measure the horizontal distance traveled by each ball. With this information, they can calculate the initial velocity. You can also have the students drop balls in the beginning to see if their answers were true to the worksheet.
- Because it is not easy to calculate exact speed by knowing motor power, have students use trial and error when launching balls to the designated area. Once students repeatedly hit the target, they should note the power level.
- Once calculations are carried out that predict how fast the ball was launched in order to get to the target area, have students identify the power-to-speed relationship.
- Repeat steps 6-9 again at another distance. Now students can calculate speed as a function of power. For example, if they hit a target "x" meters away, they calculate the speed at which the ball was launched using equations of motion and note the power level required to produce this initial speed. Then they change the power and repeat the steps with a new 'x' and speed. Then they take their first value of speed and subtract the second. Divide that by the first value of power minus the second value of power to get a relationship between speed and power, shown in Equation 5.
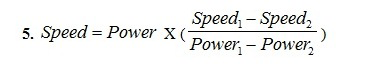
Equation 5. The relationship between speed and power. - Equation 5 represents speed in terms of the powers and speeds taken from the two measurements. Using this equation, all speeds can be calculated from the power.
- The last step is to change the target zone one more time and have students measure the distance to it, do the calculations for speed, and plug the correct power number into the code according to the Equation 5. Expect students to hit the target on the first try, which should excite them, knowing that they used math and analysis to predict future performance!
Vocabulary/Definitions
acceleration: The change in velocity with respect to time.
distance: A numerical description of how far apart objects are.
kinematics: The branch of mechanics that studies pure motion of an object without consideration of mass.
projectile: An object in motion close to the Earth's surface subject to gravitational acceleration.
projectile motion: The motion or path of a projectile.
time: A measurement of how long an event or occurrence happens.
velocity: The rate of change of an object's position. The distance traveled over a period of time.
Assessment
Pre-Activity Assessment
Real-World Examples: Ask students to name everyday examples of projectile motion and explain why they are projectile motion. Make sure they know projectile motion is based on the trajectory of objects and their motions, not inertial forces. (Example: A baseball that has been pitched, batted or thrown.)
Activity Embedded Assessment
- Observations: As students work, circulate the room to assess their progress and offer assistance where needed.
- Worksheet: Have students solve the problems on the Projectile Motion Problem Worksheet. Once they are finished, review the solutions as a class. This is a good indicator of whether students grasp the mathematical concepts behind projectile motion. Make sure that students can accurately defend why certain equations should be used to solve each problem. In addition, have students explain step by step how to use the equation(s) selected to solve for the value desired. Both students' conceptual understanding and algebraic skills are important in solving these problems.
- Performance Predictions: As part of the activity, students use two measurements of velocity and power to predict future performance of the launcher. Ask students to explain this process and describe or note any deviations from previous performance.
Post-Activity Assessment
Wrap-Up Discussion: Talk to students about what else might affect projectile motion. What forces are being neglected (such as forces of friction/air resistance/type of environmental medium)? Point out how calculated measurements are not the same as experimental and see if students provide reasonable feedback for the discrepancy (such as, the ball is hollow/very light).
Safety Issues
Watch that students do not shoot the balls at people.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to the physics concepts of air resistance and launch angle as they apply to catapults. This includes the basic concepts of position, velocity and acceleration and their relationships to one another. They
Copyright
© 2013 by Regents of the University of Colorado; original © 2012 Polytechnic Institute of New York UniversityContributors
Zachary Nishino; Ronald PovedaSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Additional support was provided by the Central Brooklyn STEM Initiative (CBSI), funded by six philanthropic organizations.
Last modified: October 16, 2020






User Comments & Tips