Quick Look
Grade Level: 9 (9-11)
Time Required: 45 minutes
Lesson Dependency:
Subject Areas: Algebra, Physical Science, Physics
NGSS Performance Expectations:

| HS-PS3-3 |

Summary
Students are introduced to the physics concepts of air resistance and launch angle as they apply to catapults. This includes the basic concepts of position, velocity and acceleration and their relationships to one another. They use algebra to solve for one variable given two variables.Engineering Connection
Engineers must fully understand basic science and math principles to design safe and effective devices. Understanding the physics of air resistance and launch angles applies to a wide variety of real-world situations such as vehicle design for fuel economy (cars, boats, airplanes, bicycles), weather pattern prediction, air duct systems, wind breaks, skydiving parachutes, athlete body position and gear, and launching satellites, weather balloon, rockets and data collection probes into the upper atmosphere and deep space, and precisely landing spacecraft and shuttles — as well as a shot from a catapult.
Learning Objectives
After this lesson, students should be able to:
- Describe air resistance and its importance in engineering design.
- Explain the importance of different launch angles.
- Calculate the position of an object given its velocity and acceleration.
- Explain the use of science and math in engineering projects.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS3-3. Design, build, and refine a device that works within given constraints to convert one form of energy into another form of energy. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Design, evaluate, and/or refine a solution to a complex real-world problem, based on scientific knowledge, student-generated sources of evidence, prioritized criteria, and tradeoff considerations. Alignment agreement: | At the macroscopic scale, energy manifests itself in multiple ways, such as in motion, sound, light, and thermal energy. Alignment agreement: Although energy cannot be destroyed, it can be converted to less useful forms—for example, to thermal energy in the surrounding environment.Alignment agreement: Criteria and constraints also include satisfying any requirements set by society, such as taking issues of risk mitigation into account, and they should be quantified to the extent possible and stated in such a way that one can tell if a given design meets them.Alignment agreement: | Energy cannot be created or destroyed—it only moves between one place and another place, between objects and/or fields, or between systems. Alignment agreement: Modern civilization depends on major technological systems. Engineers continuously modify these technological systems by applying scientific knowledge and engineering design practices to increase benefits while decreasing costs and risks.Alignment agreement: |
Common Core State Standards - Math
-
Solve quadratic equations by inspection (e.g., for x² = 49), taking square roots, completing the square, the quadratic formula and factoring, as appropriate to the initial form of the equation. Recognize when the quadratic formula gives complex solutions and write them as a ± bi for real numbers a and b.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Evaluate the design solution using conceptual, physical, and mathematical models at various intervals of the design process in order to check for proper design and to note areas where improvements are needed.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Technological problems must be researched before they can be solved.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Construct and compare linear, quadratic, and exponential models and solve problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Gather, analyze and interpret data and create graphs regarding position, velocity and acceleration of moving objects
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/cub_flyingtshirt_lesson01] to print or download.Introduction/Motivation
(It is recommended that you first introduce the engineering design challenge as presented in the associated activity, Flying T-Shirts. Then conduct this lesson. Then complete the activity.)
How far can you throw a t-shirt? Would it travel further if you rolled it up into a ball first? Why is that? At what angle should you throw the t-shirt? Do you think it's possible to predict how far the t-shirt will travel once it is thrown? All these questions can be answered with a little knowledge of physics. For any fun engineering challenge (like the one presented in the associated activity: to find a way to get school t-shirts up into the stands during sporting events), it takes a good understanding of science and math to be able to investigate these questions so you can make the best possible design.
So how come a t-shirt can be thrown farther if it is rolled up into a ball first? To answer this question, let's think about the concept of air resistance. Air is a fluid; therefore, it behaves like a fluid. Fluids exert forces on objects that try to move through them. To illustrate this, let's look at the behavior of water. When you move your hand through water, it is easiest to orient your hand so it resembles a thin blade gliding through the water. If you change your hand so that your palm faces forward, you notice that you must use more force to move it at the same speed as before. This is due to the water pushing on the part of your hand that is facing forward. When more surface area faces forward, then the water has more area to push on and applies more force on your hand, hence slowing down your hand.
In general, we like to exert the least amount of energy to get any job done. So, to minimize the force that the water exerts on your hand as it moves through the water, you alter the shape of your hand to minimize this force. This is the concept of making objects fluid dynamic — minimizing the force that fluids can exert on objects that travel through them. Since air is also a fluid, it exerts these same forces on objects that try to move through it.
Let's do the same experiment as before, but through air. Think about when you are in a moving car with the window down. When you stick your hand out with your palm facing forward (towards the front of the car), you feel the air pushing your hand back. If you turn your hand so that your palm faces down (your hand flat), you can feel the decrease in force pushing on your hand. Whether your hand was in water or air, you could always change its shape or orientation to make it more fluid dynamic.
Now, back to our t-shirt... How can we make the t-shirt more fluid dynamic? Well, we just learned that to achieve a more fluid dynamic object we want to minimize the surface area that the air uses to push on the t-shirt. Using that idea, we could roll up the t-shirt and constrain how much of the t-shirt is exposed to the air, which would slow it down. This would make the t-shirt be more fluid dynamic and thus travel further through the air.
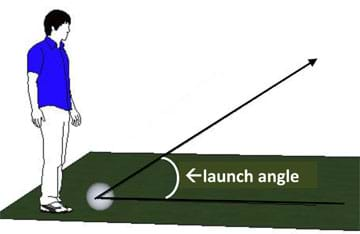
Another important science concept to understand has to do with the angle the object (our t-shirt) is thrown. This is known as the launch angle and is measured in degrees above the horizontal surface (see Figure 1). This is important if you are designing a device that throws something and you want to know where the object will land. For example, would you rather throw a shirt at a 60, a 45, or 30-degree angle if you want the shirt to fly the farthest? (The answer is 45 degrees, but don't just give the answer. To help the class answer this question, go to http://phet.colorado.edu/en/simulation/projectile-motion and use the interactive simulation that shows the trajectory and landing location of objects thrown at different angles. Since you can adjust the air resistance, it is a good tool to support the concepts of launch angle and air resistance.)
(Next, hand out the attached Launch Angle & Air Resistance Worksheet to test students' basic understanding of the concepts presented thus far.)
Understanding air resistance and launch angle are important science concepts to know for our design challenge because it will help you design the best device. It is also important to be able to predict how far your t-shirt will go. Of course, you could do this by trial and error or you could use your knowledge of physics and apply your algebra skills. The physics ideas used are position, velocity and acceleration. Position is just what it sounds like; it is the object's location and is usually measured in meters (m). Velocity is the speed the object is traveling at and what direction it is going; this is measured in meters per second (m/s). Acceleration is how much the velocity is changing (is the t-shirt speeding up? or slowing down?), and is measured in meters per second squared (m/s2). If you know the velocity and the acceleration, you can calculate the position of an object using the following equation: (write this equation on the board)
where
p = position at time t (m)
po = starting position (m)
vo = starting velocity (m/s)
a = acceleration (m/s2)
t = time (s)
This particular equation is a little too simple to be able to help much with our design challenge, but it can be used for a lot of simple situations and it helps show us how science and math are used in engineering design.
(Next, hand out the attached Position, Velocity & Acceleration Physics Worksheet as an in-class assignment or as homework. It offers some problems to be solved using the equation.) All engineers need a basic understanding of science and math fundamentals like theses in order to create the best designs possible.
Now how can we use what we've learned about launch angles and air resistance as we create engineering designs for our Flying T-Shirts challenge? (Lead a class discussion. Proceed to conduct and complete the associated activity with the class.)
Lesson Background and Concepts for Teachers
The purpose of the lesson is to introduce the students to some science concepts related to the engineering design challenge in the associated activity — Flying T-Shirts. While the activity's design project could be completed without the lesson, it is an excellent opportunity to cement students' understanding of some key science and math concepts and show them how engineering uses science and math. We suggest you introduce the design challenge — to find a way to get school t-shirts up into the stands during sporting events — and then conduct the lesson.
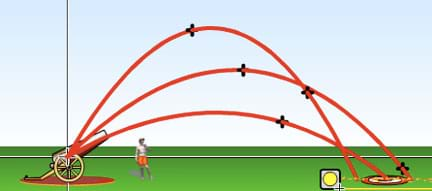
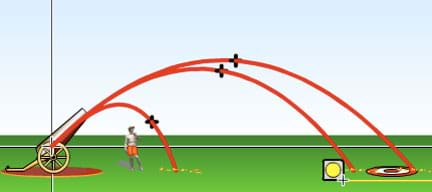
Make use of an excellent projectile motion interactive simulation available at PhET Interactive Simulations, University of Colorado, http://phet.colorado.edu/en/simulation/projectile-motion, which shows the resulting trajectories when you set the launch angle, initial speed, mass and air resistance. Some launch angle and air resistance examples are shown in Figures 2 and 3.
Another air resistance classroom demo: Get a textbook and a piece of paper that is the same size as the textbook cover. Hold the sheet of paper and the textbook horizontal to the ground and drop them at the same time. The sheet of paper hits the ground much later than the book. Then place the sheet of paper on top of the book and drop them at the same time. This time, the sheet of paper falls at the same speed as the book. This is because the textbook moves the air out of the way so air resistance does not affect the paper.
Associated Activities
- Flying T-Shirts - Students are given the design challenge of getting school t-shirts up into the stands during sporting events. They use the engineering design process to investigate possible solutions, build a usable prototype and keep it under budget.
Lesson Closure
Who can give me an example of how math and/or science are used in engineering design projects. (Listen to student suggestions. Add to their suggestions with real-world examples provided in the Assessment section.)
In our Flying T-Shirt design challenge, what were some of the science and math concepts that were important to understand? (Answers: Launch angle, air resistance, position, velocity, acceleration, and algebra — for the equation.) Does it make a difference what angle we launch an object from a catapult? What is air resistance? Can you think of items that engineers have designed to be aerodynamic? Or maybe designed to not be aerodynamic (such as parachutes!)?
Vocabulary/Definitions
acceleration: Change in the velocity of an object.
air resistance: The resistance to motion caused by objects moving in air.
fluid dynamic: Minimizing the force that fluids can exert on objects that travel through them by changing the shape or orientation of the object. When the fluid is air, this is termed aerodynamic.
launch angle: The angle from the horizontal (ground) to initial direction of the object.
position: The location of the object.
velocity: The speed and direction of an object.
Assessment
Pre-Lesson Assessment
Class Discussion: Have the class discuss the importance of science and math in engineering, giving real-world examples. Add to their ideas with these additional examples. Engineers:
- understand the concepts of forces and materials science to design skyscrapers and bridges that are safe under many types of loads and weather conditions
- use geometry principles to design navigation equipment and land probes on faraway planets
- use an understanding of electrons to design computers and music players
- applying chemistry to solve environmental pollution problems and design useful products like glue, paint, cleaning products and bubblegum
- use an understanding of electricity and magnetism to design medical devices such as non-invasive body scanning MRI machines
- use mathematics and logic to write programming for the software we use every day
- understand life science and chemistry to create replacement human tissue and body parts
- use the mechanics of movement to design everything from hinges to amusement park rides
- use algebra to make energy calculations
- use air resistance and launch angles to design rockets to go the furthest and land on target with the least amount of fuel
Post-Introduction Assessment
Worksheets: Have the students complete the attached two worksheets; review their answers to gauge their mastery of the subject.
Lesson Summary Assessment
Class Discussion: Have the class discuss how they can use the concept of air resistance and launch angle in their designs for the "Flying T-shirts" activity.
Lesson Extension Activities
Conduct the sixth-grade Catapults! activity at https://www.teachengineering.org/view_activity.php?url=https://www.teachengineering.org/collection/cub_/activities/cub_mechanics/cub_mechanics_lesson04_activity1.xml
Conduct the seventh-grade Magician's Catapult activity at https://www.teachengineering.org/view_activity.php?url=https://www.teachengineering.org/collection/cub_/activities/cub_simp_machines/cub_simp_machines_lesson04_activity1.xml
Additional Multimedia Support
Learn about projectile motion by firing various objects. Set the angle, initial speed, and mass. Add air resistance. Make a game out of this simulation by trying to hit a target. See the PhET Interactive Simulations from the University of Colorado at http://phet.colorado.edu/en/simulation/projectile-motion
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn about catapults, including the science and math concepts behind them, as they prepare for the associated activity in which they design, build and test their own catapults. They learn about force, accuracy, precision and angles.

Students learn about the fundamental concepts important to fluid power, which includes both pneumatic (gas) and hydraulic (liquid) systems.

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...
Copyright
© 2008 by Regents of the University of Colorado.Contributors
Jonathan MacNeil; Scott Duckworth; Brandi Jackson; Stephanie Rivale; Denise W. CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: January 6, 2021








User Comments & Tips