Quick Look
Grade Level: 5 (4-5)
Time Required: 1 hour
Lesson Dependency: None
Subject Areas: Physical Science, Science and Technology
NGSS Performance Expectations:

| 5-PS2-1 |

Summary
Students learn about catapults, including the science and math concepts behind them, as they prepare for the associated activity in which they design, build and test their own catapults. They learn about force, accuracy, precision and angles.Engineering Connection
Engineers must master the science and math concepts behind a given technology before they can successfully design and build products that meet their clients' needs.
Learning Objectives
After this lesson, students should be able to:
- Describe how force affects the motion of a projectile.
- Explain and compare the meanings of accuracy and precision.
- Explain the optimum angle for launching a projectile the farthest distance (45 degrees).
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
5-PS2-1. Support an argument that the gravitational force exerted by Earth on objects is directed down. (Grade 5) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Science explanations describe the mechanisms for natural events. Alignment agreement: | The gravitational force of Earth acting on an object near Earth's surface pulls that object toward the planet's center. Alignment agreement: | A system can be described in terms of its components and their interactions. Alignment agreement: |
Common Core State Standards - Math
-
Geometric measurement: understand concepts of angle and measure angles.
(Grade
4)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Use concepts of angle and measure angles.
(Grade
4)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/cub_catapult_lesson01] to print or download.Introduction/Motivation
Today we are going to learn all about catapults and the important math and science concepts behind them. We are preparing for an activity we will get to do very soon, during which we will design and build our own catapults. Like engineers following the engineering design process, before we begin designing or building, we must research catapults and learn as much as we can about them.
Who has heard of catapults? What do they consist of? (They consist of a lever and a wheel-and-axel.) What are catapults used for? (Listen to student ideas and experiences.) Originally catapults were designed for use during battles or wars. These days, catapults are used for a variety of reasons, from toys to even launching planes and jets from aircraft carriers that have limited runway space!
Let's say we want our catapults to launch Ping-Pong balls at a certain target. If we are trying to hit targets with the catapults, we need to discuss a few science concepts. One concept is force. How do you think force affects the speed of the Ping-Pong ball and the distance it travels? (Answer: More force means more speed and more distance.) The more force you apply to a catapult, the more force is applied to the object being launched. Think of the simplest type of catapult possible: a plastic spoon. If you've ever launched something from a plastic spoon (hopefully not food at your brother or sister!), you might know that if you add more force by pulling the top of the spoon back farther, the projectile goes faster and farther. A slingshot provides another example. The more force you apply by pulling back the rubber band on the slingshot, the bigger the force applied to the projectile. This means the projectile will go faster and farther. Following the lesson, challenge students to complete the associated activity Right on Target: Catapult Game to build accurate and precise catapults using simple materials.
Lesson Background and Concepts for Teachers
(Optional: show the attached Engineering Fun! Catapult Presentation. Consider reviewing the following information during the presentation. Have students answer questions on the Engineering Fun! Catapult Presentation Notes while going through the slides.)
Slide 1: When you hear the word "catapult," you might only think of devices that were used during battles in the Middle Ages. But even today, catapults are used for many different purposes. Did you know that they are used to launch planes on aircraft carriers where runway space is limited? Engineers have found many useful and fun modern applications for this ancient technology!
Slide 2: To make a projectile cover the most horizontal distance possible, it should be launched from a 45º angle. Remember this fact because you will need to apply it to the construction of your catapults in the upcoming activity. If a projectile is launched from an angle greater than 45º, where will it go? (Answer: It will go higher, but not cover as much horizontal distance.) If the same projectile is launched from an angle less than 45º, where will it go? (Answer: It will not go as high and therefore is pulled to the ground more quickly by gravitational force, and thus, falls short.) Now let's talk about force. In the picture on the screen, do you think the string that is wrapped around the spoon-shaped part should be really tight or really loose? (Answer: Tight.) If the string is tight, do you think more or less force is applied to the projectile or object? (Answer: More force.)
Slide 3: These four pictures help un undertand the concepts of accuracy and precision. In the top left picture, none of the shots are very close to the bull's-eye or to each other. That means the shots are neither accurate nor precise. In the top right picture, the shots are closer to the bull's-eye, which means the accuracy is getting better, but they are not close to each other (meaning they are not precise). In the bottom left picture, the shots are all close together, meaning they are precise, but they are not close to the bull's-eye, so they are not accurate. And finally, in the bottom right picture, all the shots are close together and hit the bull's-eye. That means they are both accurate and precise!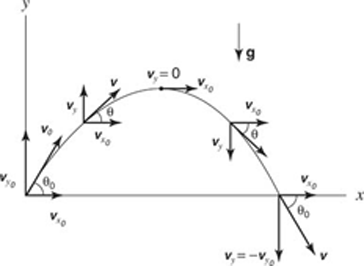
Slide 4: Why are we learning all this? Well, we are about to do a really fun activity. Here's a sneak peak at what's to come in the activity. We will be designing and creating a catapult to launch Ping-Pong balls. Once the catapults are built, we will play a game where we aim for targets. These are some of the materials that you will use. Now you know why it is important that we learn all this information and take notes!
Projectile motion refers to the motion of an object projected into the air at an angle. Galileo was the first person to accurately describe projectile motion by analyzing the horizontal and vertical components separately. Two important equations exist for position in projectile motion with no friction. While these equations are not required in order to teach the lesson, they demonstrate how projectile motion can be broken down into two components and show the relationship between horizontal or vertical distance, time, and the angle at which the projectile is launched. The first equation gives the horizontal position of the projectile as a function of time and the second one gives the vertical position of the projectile as a function of time. The variable x refers to the horizontal position, and y refers to the vertical position, the variable t refers to the time that has passed since the projectile was launched (t=0 refers to the time when the projectile is launched) and θ refers to the angle at which the projectile is launched.
(1) x(t) = x0 cos(θ) t
(2) y(t) = x0 sin(θ) t - (1/2) gt2
Galileo reasoned that a projectile is not only influenced by one motion, but by two. The motion that acts vertically is the force of gravity, and this pulls an object towards the Earth at 9.8 meters per second. But while gravity is pulling the object down, the projectile is also moving forward (horizontally) at the same time. This horizontal motion is uniform and constant according to Galileo's principle of inertia. He was able to show that a projectile is controlled by two independent motions that work together to create a precise mathematical curve. He found that the curve has an exact mathematical shape called the parabola. Galileo concluded that the path of any projectile is a parabola (see Figure 1).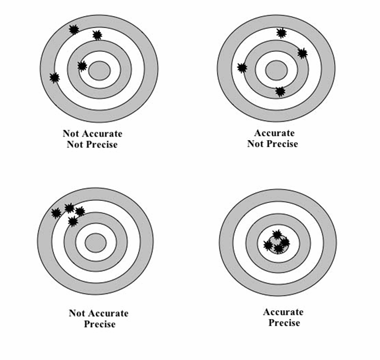
A parabola is a symmetrical curve, meaning that the downward trip of a projectile is a mirror image of the trip up. To make a projectile cover the most horizontal distance possible, it must be launched from a 45º angle. If a projectile is launched from an angle greater than 45º, it goes higher, but does not cover as much horizontal distance. If the same projectile is launched from an angle less than 45º, it will not go as high and therefore will be pulled down to the ground more quickly by gravitational force. Interestingly, if the horizontal distance vs. the angle at which the projectile is launched was graphed, it would give a symmetrical graph. This means that a projectile launched at 30° has the same range as one launched at 60°.
The Figure 2 diagram is helpful to review with students the concepts of accuracy and precision. Accuracy describes the nearness of a measurement to the standard or true value. Precision is the degree to which several measurements provide answers very close to each other. To get a better understanding of accuracy and precision and how they relate to the catapult activity, consider the example of shooting arrows at a bull's-eye target. In this example, accuracy describes the closeness of arrows to the bull's-eye at the target center. Arrows that strike closer to the bull's-eye are considered more accurate. The closer a system's measurements to the accepted value, the more accurate the system. Precision relates to whether or not the arrows hit the target in the same place. When all arrows are grouped tightly together, the cluster is considered precise since they all struck close to the same spot. The arrows do not need to hit the bull's-eye (or even the target) to be precise.
Associated Activities
- Right on Target: Catapult Game - Students experience the engineering design process and build accurate and precise catapults using simple materials. They use their catapults to participate in a game in which they launch Ping-Pong balls and attempt to hit various targets.
Lesson Closure
Today we learned so much! We talked about catapults and the important science and math concepts crucial to engineering our own catapults. What do you think we should do next? You guessed it – we are ready to design, build and test our own catapults!
Vocabulary/Definitions
accuracy : The degree of closeness of a measured or calculated quantity to its actual (true) value. For example, in the associated activity, accuracy is the ability to hit the target with the Ping-Pong ball.
catapult: A toy/machine that launches a projectile.
geometry: An area of mathematics that studies shape, size, position and properties of space.
precision: The degree to which further measurements or calculations show the same or similar results. For example, in the associated activity, precision is the ability to hit the same location multiple times with the Ping-Pong ball.
projectile: An object that is launched or thrown, usually in the air, by a force.
quadrilateral: A polygon with four sides. Examples include squares, rectangles, and trapezoids.
triangle: A polygon with three sides.
Assessment
Pre Assessment:
Catapult Pre-Lesson Quiz: Students complete the Catapult Quiz to assess prior knowledge about catapults, projectile angles, accuracy, precision and force.
Lesson-Embedded Assessment:
Note-Taking: Have students complete the Engineering Fun! Catapult Presentation Notes during the Engineering Fun! Catapult Presentation.
Post Assessment:
Catapult Post-Lseson Quiz: At lesson end, have students complete the Catapult Quiz again to assess what they learned. Compare pre/post answers to gain an understanding of how much students understood and retained from the lesson.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to the physics concepts of air resistance and launch angle as they apply to catapults. This includes the basic concepts of position, velocity and acceleration and their relationships to one another. They

Students experience the engineering design process as they design and build accurate and precise catapults using common materials. They use their catapults to participate in a game in which they launch Ping-Pong balls to attempt to hit various targets.

Students learn how engineers navigate satellites in orbit around the Earth and on their way to other planets in the solar system. In accompanying activities, they explore how ground-based tracking and onboard measurements are performed.

Students investigate error in the context of navigation because without an understanding of how errors can affect your position, you cannot navigate well. Introducing accuracy and precision develops these concepts further. Also, students learn how computers can help in navigation.
Copyright
© 2011 by Regents of the University of ColoradoContributors
William Surles; Jake Crosby; Jonathan McNeil; Malinda Schaefer Zarske; Carleigh SamsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: April 22, 2021









User Comments & Tips