Lesson Accuracy, Precision and Errors in Navigation:
Getting It Right!

Learning Objectives

• Explain that mathematical concepts are required when navigating.
• Describe the difference between accuracy and precision.
• Explain the value computers have on society and describe the advantages as well as disadvantages of using a computer.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Introduction/Motivation

Often, how well we "do" an activity is very important. For example, if you are playing baseball and your teammate is not good at throwing you the ball, you might have to run more to get the ball. In fact, in a real game, your team might lose a couple of runs because of your teammate's lack of skill. The difference between where your teammate is supposed to throw the ball (to your glove) vs. where they actually throw the ball (somewhere in left field) is called the error. When is error too much? (Answer: each situation is different; it depends on the result of the error.) If your teammate successfully throws the ball at you, but it's short, is that error okay? When is the error large enough to be a problem? (Possible answer: when the throw is off so much that you cannot reach the ball to make an effective play.)

Precision and accuracy play an important role when navigating. Even when you think you know where you are going and are not actively using math, you are probably using simple geometric concepts in your head. Mathematical concepts are inherent in navigation, but writing down equations or using a computer to do math is not usually necessary in our everyday lives. In some cases, though, we need to find places that are very far away, we need to find a spot as quickly as possible, or we need to be exact about a location. Doing the math in our heads or on paper can take a long time. Computers can help do that necessary math.

Lesson Background and Concepts for Teachers

Major improvements to navigation initially involved creative mathematical thinking and engineering. Before computers existed, engineering was the prime tool to make navigation easier. The sextant, a device used to determine latitude and longitude, used angled mirrors, graduated scales, and sturdy materials to make astronomical measurements much more accurate than previous methods. The sextant is a convenient, reliable, and accurate tool still used today. Even the sextant can use the assistance of computers when they are available.

Currently, we take computers and calculators for granted. We use them to help us with our homework, play games and even talk to friends. It was only 25 years ago that buying a calculator cost over $500, and desktop computers, like the ones in your classroom, school lab, or home, did not even exist.

Before computers, the math needed to perform accurate navigation had to be done either by hand or by looking up information in tables, a very tedious task and prone to errors. Today, luckily, we have computers and calculators to help us with math. Computers are very fast at figuring out calculations and repeating tasks, but we still need to understand how the math works so that we can efficiently use the computer. Electrical engineers and computer scientists write the programs that help us in our daily use of computers. Although computers help you complete difficult tasks easier, you still need know how things work so that you can tell the computer what to do and verify that your results make sense.

Accuracy and Precision in Measurement

There are two basic concepts to any collection of measurements, accuracy and precision (Refer to the activity Close Enough? Angles & Accuracy of Measurement in Navigation activity to practice these two concepts). Accuracy is how close the measured data is to the actual value. For example, if you know that you have a mass standard that is 50.00 grams, and you measure it to be 49.98 grams, then your measurement is very accurate. On the other hand, if you measure it to be 43.24 grams, your measurement is not very accurate.

Precision is how close your measurements are relative to each other, not the actual value. For example, let say you measured that same mass standard and came up with the values:

43.24, 43.30, 43.20, 43.25, 43.32

You could say that your measurement was very precise because all the values are very close to each other. On the other hand, if your measurements were:

50.03, 43.40, 53.01, 47.54, 30.23

Your measurements would not be very precise because they are all far apart relative to each other.

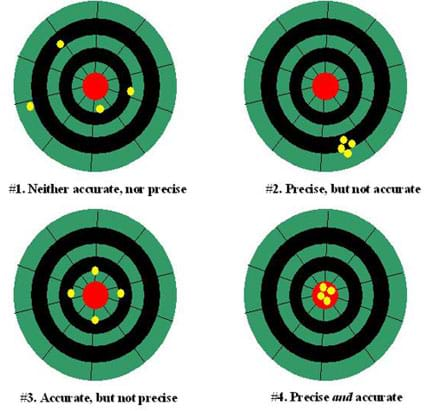
A dartboard is a common example of showing the difference between accuracy and precision (please see Figure 1). Assume that someone throws four darts at a dartboard. If they are far apart and unevenly spaced, they have neither precision nor accuracy (#1). The closer the darts are to the center, the better accuracy they have. The closer the grouping of darts is to one another, the better precision they have (#2). If the darts are evenly spread around the center, the dart thrower has low precision but high accuracy — they are not close to each other but all of the darts are equally far from the center (#3). And finally, if all of the darts are closely grouped in the center of the dartboard, the thrower has both high accuracy and precision (#4) because the darts are either on or very close to the target.

Tabulating Machines

In the 1880s, it was estimated that the next American census in 1890 would need to tally data from more than 62 million Americans. This was not only expensive, but the existing system of tallying marks in small squares on rolls of paper and then adding the marks by hand was extremely time consuming. Workers realized that continuing to take the census with this method would be impossible and that, somehow, the system would have to be automated.

An American inventor, Herman Hollerith, developed the solution to this problem. Cards punched by a tram conductor's ticket punch were fed into a mechanism that could read the presence of holes in each card by using spring-mounted nails that passed through the holes to make electrical connections. The electrical connection would then move a clock-like counter that accumulated the results.

In addition to solving the census problem, Hollerith's machines were useful for a wide variety of statistical applications. Subsequently, these same techniques were significant in the development of the computer. In February 1924, Hollerith's company changed its name and continued to grow; in fact that compnay is still around today. It is very unlikely you have not heard of it: International Business Machines. Does it ring a bell? Perhaps you know it by its initials: IBM. Use the activity Computer Accuracy to have students investigate the significance of accuracy in current day machines.

Old and New Techniques

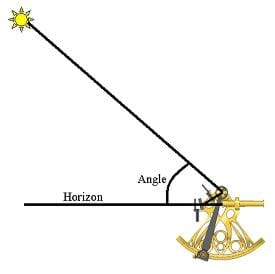
The sextant is a complex device, but luckily it is very easy to use. Students can practice modern applications of the sextant in the activity Sextant Solutions. Basically, a sextant measures the angle between two objects, with at least one of those objects being celestial. (Remember, never look directly at the sun, as permanent damage can occur to the eye! Shields and filters on sextants protect against eye injuries.) The user looks through the sextant's eyepiece directly at the first object (usually the horizon). There is actually a mirror in the line of sight, but because it is only partially silver, the user can see beyond it (to the horizon). The other mirror is connected to a movable arm and directs light from the second object (usually the sun or moon) and reflects it into the half-silvered mirror. The movable arm is adjusted until you can see both the first object (the horizon) and the second object (the sun or moon), overlaid on top of each other. Finally, you read the measurement of the angle, which is located on the movable arm.

The most common use of a sextant is measuring the angle between the horizon and the sun. By knowing this angle and your local time, your latitude can be determined. If you also know the Greenwich Mean Time (GMT), your longitude can also be determined.

Associated Activities

• Close Enough? Angles & Accuracy of Measurement in Navigation - The concept of accuracy in measurement is introduced; students will learn about the difference between accuracy and precision. Using a computer, they will see how much accuracy is needed for various activities. If going to the moon, one needs to have a very accurate flight path or the moon might be missed completely!

  Watch this activity on YouTube

• Computer Accuracy - Using an MS Excel® spreadsheet, students will see how small errors can drastically affect their results, which is a real issue for navigators. Students will learn how a small angle error in their course will change their final landing point.

  Watch this activity on YouTube

• Sextant Solutions - Students use an MS Excel® spreadsheet to facilitate complicated corrections for a sextant measurement. They will see how computers can help us work more effectively with complex calculations as they compute detailed corrections for a sextant measurement.

Lesson Closure

Computers are taken for granted today. They are smaller and pack more power every year. Understanding how computers fit into the world is important even if you do not want to know how they work. Recognizing how concepts of navigation are facilitated by computers is a step in the right direction. It is also important to recognize the importance of learning and understanding the mathematical concepts that precede the computing. Only when understanding how right triangles can be used, when curved lines can be considered flat, and when to keep a curved line to increase accuracy can you use a computer to its fullest advantage.

Vocabulary/Definitions

Accuracy: A measure of how close the data comes to the correct answer.

Altitude : The angle between two points. For example, the angle between the horizon (on the ground) and the sun.

Computer: A programmable device that processes information.

Equation: A statement usually written as symbols, which are separated into left and right sides and joined by an equal sign.

Geometry: The mathematical relationships of points, lines, angles, surfaces and solids.

Precision: A measure of how close the data points are relative to each other. In other words, how well grouped your data set is.

Sextant: A navigational instrument containing a graduated 60-degree arc, used for measuring the altitudes of celestial bodies to determine latitude and longitude.

Trigonometry: The mathematical relationships between the sides and the angles of triangles.

Assessment

Pre-Lesson Assessment

Discussion Questions: Solicit, integrate and summarize student responses.

• Computers are everywhere, but do we really need computers? Do you need a computer to tie your shoe? Can a computer help you brush your teeth? Are computers required for navigation? What do you think?

Post-Introduction Assessment

Voting: Ask a true/false question and have students vote by holding thumbs up for true and thumbs down for false. Count the votes, and write the totals on the board. Give the right answer.

• True or False: With enough time and supplies, you could navigate anywhere in the world without the help of a computer. (Answer: True, but you would have to have A LOT of time.)

Lesson Summary Assessment

Voting: Ask a true/false question and have students vote by holding thumbs up for true and thumbs down for false. Count the votes, and write the totals on the board. Discuss the answer.

• Computers are not absolutely necessary for navigation, but after this lesson, who thinks they are a good idea? Why? Why not?

Bingo: Provide each student with a sheet of paper containing a list of the lesson vocabulary terms. Have each student walk around the room and find a student who can define one vocabulary term. Students must find a different student for each term. When a student has all terms completed s/he shouts "Bingo!" Continue until two or three students have bingo. Ask the students who shouted "Bingo!" to give definitions of the vocabulary terms.

Lesson Extension Activities

A sextant can measure many objects; below are instructions for determining latitude. Using a sextant, follow the steps below to determine your latitude (and longitude):

1. Do at exactly noon, when the sun is at the highest point during the day.
2. Look through the sextant's eyepiece.
3. Adjust the angle of the sextant until you see the horizon.
4. Now adjust the movable arm until you see the sun. Because you should never look at the sun directly, the sextant has a number of filters that will block out most of the sun's light, but will let enough through to still see it. Make sure to always use the filters so that you do not hurt your eyes.
5. Adjust the arm until the sun rests just on the horizon.
6. Now measure the altitude of the sun by reading the angle on the movable arm.
7. Write down the exact local time.
8. Determining Longitude Option: Write down the exact GMT (Greenwich Mean Time).

The above steps give you all the information you need to find your latitude and longitude. Knowing that the measurement was taken when the sun was at its highest point in time, you know that it was noon. This, and the angle of the sun off of the horizon, can tell you your latitude. If you also did Step 8, you could determine your longitude. Knowing the GMT time and the time where you are tells you the difference in time between your location and Greenwich, England (zero degrees longitude). You can relate this time difference to the distance and find your longitude. To actually compute your latitude and longitude, you need to do a number of long calculations — another way that computers can help.

For students with web access, the following PBS site has a great shockwave-based interactive story that lets you try simplified sextant readings and learn about the amazing survival of Shackleton and his crew: http://www.pbs.org/wgbh/nova/shackleton/navigate/escape.html

Have students research the story of Apollo 13 and perform the calculations — without computers! — that the astronauts had to do in flight to save their lives.

References

Other Related Information

Scaling

• For 6th grade, have students complete the associated activities "Close Enough" and "Computer Accuracy."
• For 7th and 8th grade, have students complete the associated activities "Close Enough" and "Sextant Solutions."

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.