Hands-on Activity You've Got Triangles!

Learning Objectives

After this activity, students should be able to:

• Define a right triangle.
• Measure distances by using a ruler, yardstick or ultrasonic sensor.
• Measure angles and estimate angles using a protractor.
• Estimate the height of various objects by creating a 45° right triangle with a known base.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

Each group needs:

• protractors, one per student
• Triangles Activity Assessment, two per student (pre/post)
• Triangles Activity Worksheet, one per student

To share with the class:

• LEGO MINDSTORMS EV3 robot, such as EV3 Core Set (5003400) at https://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3; alternatively, if enough LEGO robot kits are available, provide one for each student group, instead of sharing one kit with the entire class.
• computer with USB cable, to download and transfer ev3 file
• painters tape, or other tape suitable to mark a triangle shape on the classroom floor
• a stack of textbooks, to use to line the triangle shape taped on the floor
• a class set of rulers, yardsticks or meter sticks

Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:

• LEGO MINDSTORMS NXT Base Set

Worksheets and Attachments

Pre-Req Knowledge

• Familiarity with different types of triangles, including right triangles and 45-45-90 triangles (45-degree right triangle).
• Ability to measure length using a ruler or yardstick and angle degrees using a protractor.
• Some practice with estimation.

Introduction/Motivation

Trigonometry is the study of triangles and the relationship between their angles and sides. In a triangle, each pair of sides forms an angle less than 180°. Since a triangle must be closed, meaning all the sides meet another side at each endpoint, the sum of three angles of a triangle must be equal to 180°. Amazingly, this characteristic is the reason why triangles are incredibly strong and often used in structures. Engineers and builders use triangles frequently in the process of designing and constructing buildings and other structures.

Triangles are also used to define or calculate relationships between different parts of a structure. For example, a typical pitched roof is usually made of wooden or steel trusses in the shape of triangles. Sometimes, however, it is not easy or physically possible to measure the actual distance between objects. Therefore, a variety of electronic instruments are often used to measure distances that are too hard to reach or extremely long. The ancient Egyptians standardized a measurement unit termed cubit, equal to the length of the arm of a royal master from the elbow to the end of the fingers (approximately 18 inches or 46 cm), and used it to build accurate structures such as the pyramids.

Furthermore, in many everyday life situations and on work sites, it is quite useful to estimate distances. Estimation is the process by which we take an educated guess as to what the real value of an object is, without measuring the exact value. For example, we can estimate the height of a person to be five feet even without using a ruler or yardstick. What else might we estimate, besides distances? (Listen to student ideas.) We might estimate the cost of buying a new car, or a person's age. During this activity, you will get to practice your estimation and measurement skills with the help of trigonometry, and also learn about the role of trigonometry in real-world problem-solving.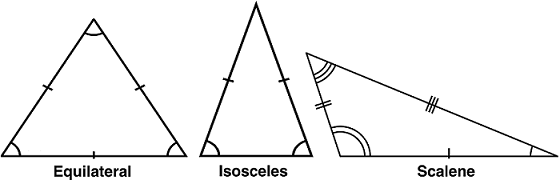

To begin, let's review the following basic concepts of triangles. First, let's consider different types of triangles based upon the length of the sides. (Draw the Figure 1 triangles on the classroom board as you describe the triangle types.) For example, an equilateral triangle is a triangle in which all three sides are the same length, resulting in each of its angles being 60°. An isosceles triangle is a triangle with two equal sides, resulting in two angles of this triangle being the same. And a scalene triangle is composed of sides of three different lengths resulting in all three angles of the scalene triangle being different.

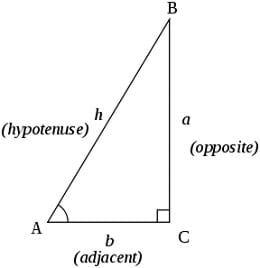
Next, let's examine triangles based upon their angles. A right triangle, which has one angle equal to 90°, is a special type of triangle that has names for each of its sides: hypotenuse (longest side), base and height. In any box-shaped room, two adjoining sides, such as the floor and a wall or two adjoining walls, form two sides of a right-angle triangle making a 90° angle between them. If you were to draw an imaginary diagonal line between the floor and the ceiling, a right triangle is created. How can we find out if a triangle is a right triangle? One way is to use a protractor. This is an instrument used to measure the angle between two lines. It works by having a fixed base and a rotating arm that can be lined up with the second line. The markings on the protractor then line up with the rotating arm and tell us what angle is formed.

Now that you know how a protractor works, let's start the activity to learn more about estimating and measuring using triangles and trigonometry.

Procedure

Before the Activity

• Make copies of the Triangles Activity Assessment and the Triangles Activity Worksheet.
• Using the LEGO kit, prepare the Five Minute Bot using the instructions at https://www.youtube.com/watch?v=Dhe2jXi3Fc4.
• Place tape on the floor in the shape of a right isosceles triangle with a base of 36 inches. Line text books vertically along the tape to form walls, as shown in Figure 4.
• Program the robot using GoProgram, which makes the robot travel a set distance, equal to the length of the base of the triangle taped on the floor. Download the ev3 file to a computer with the LEGO MINDSTORMS EV3 software. Then hook up the robot to this computer using a USB cable. Finally, use the LEGO MINDSTORMS EV3 software to download the program to the robot.

With the Students

1. Introduction: Administer the pre-activity assessment.
2. Discuss the concepts of triangles, types of triangles, measurements and estimating, as presented in the Introduction/Motivation section.
3. Hand out the worksheets.
4. Direct students to answer the following question on their worksheets: Challenge Question: How can we estimate the height of an object?

   

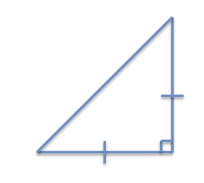
5. Comprehension: To make sure that students understand the characteristics of different types of triangles, demonstrate calculating the height of a triangle on the classroom board. Do this in an interactive way that involves students' participation.
6. Draw a right isosceles triangle on the board, as shown in Figure 2.
7. Place hash marks on the two equal sides to indicate that they are equal in length.
8. Measure the length of the base of the triangle with a yardstick or meter stick and write it next to the base for students to see.
9. Ask students to pretend they are engineers working on a design of a triangular building (shown in Figure 2 and on the board), and need to identify the type of triangle in the design.
10. Once students correctly identify it as a 45° right triangle, also known as a 45-45-90 triangle, ask them how they could calculate the height of the triangle.
11. Guide students towards the correct answer: the height of a 45° right triangle is the same as the length of its base.
12. Repeat this process using a scalene right triangle. Clarify that if the triangle is not a 45° right triangle, the height must be physically measured and cannot be assumed based on the length of the base.

    

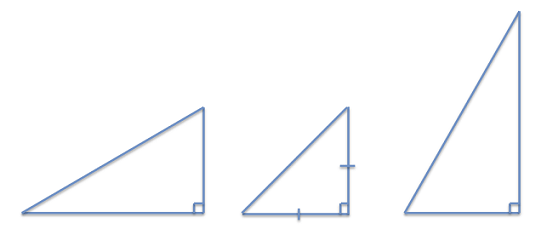
13. Application: Draw three right triangles on the board, as shown in Figure 3.
14. For each triangle, give the length of the base of the triangle. Do this by either measuring the base or assigning a randomly chosen value.
15. Ask students to estimate the lengths of the heights of the triangles. Some of the triangles have 45° angles and others do not.
16. For each estimate, ask students to explain their reasoning, based on the lengths of the sides in the triangle. For example, students may notice that the triangle on the left in Figure 3 appears to be a little less than double the length of the height.
17. Next, ask students to estimate the height of the ceiling in the classroom by using the following estimation process:

• Have students sit on the ground, each holding out a protractor at a 45° angle.
• Ask them to move backwards or forwards until they find a spot where the straight edge of the protractor is pointing right at the intersection of the wall and ceiling.
• Once students find this spot, have them to raise their hands. Bring students with raised hands a piece of tape to mark the spot on the floor.
• Have students work in pairs or groups of three to measure the distance between each student's spot and the wall.
• Using the analogy of a 45° right-angle triangle, students estimate the height of the ceiling. In this analogy, the distance from where they are sitting to the wall represents the length of the base of the triangle.
• Have students record their estimates on their worksheets and compare results with one another.

  

18. Analysis: Direct the class's attention to the right isosceles triangle prepared before the activity by marking on the floor with tape and surrounding it with textbook walls (see Figure 4).
19. Have students place the robot at the corner formed by the hypotenuse and the base of the triangle such that it travels along the base of the triangle upon the program execution.
20. When the program terminates, within some experimental tolerance, the robot should reach the corner formed by the triangle's base and height.
21. Next, have a student rotate the robot 90° and run the same program again.
22. Then have a student rotate the robot 45° and have the robot travel along the hypotenuse.
23. Through this visual experimentation, students verify that the two sides of a right angle isosceles triangle are equal, and the third side is longer.
24. Ask students to use their observations from the experiment to make inferences about any differences they noticed between the actual height of the triangle and their estimates.
25. Ask students to form into groups of two or three students to brainstorm and discuss what other things can be estimated with the trigonometry technique that they have learned. Possible answers: the heights of buildings, skyscrapers, bridges, trees, cell towers and homes.
26. Ask students why they think using an electronic sensor or math for measurements might work better than a yardstick when building a skyscraper. Ask them to imagine engineers trying to measure the height of a skyscraper with a yardstick! Ask them to discuss ideas about how to estimate the height of a suspension bridge or the height of a building based on the shadow it casts, for example.
27. Finally, ask students to end their discussion with the consideration of measuring even more distant objects by using more complex geometry or other types of sensors; for example, the distance from one city to another or the distance to the moon or sun.
28. Synthesis: Ask students to imagine that they are construction workers standing at the top of a building on a construction site. Ask them what they would do to estimate the horizontal (ground) distance from the top of their building to another building or tree near the construction site, assuming that they know the height of the building they are on.

    

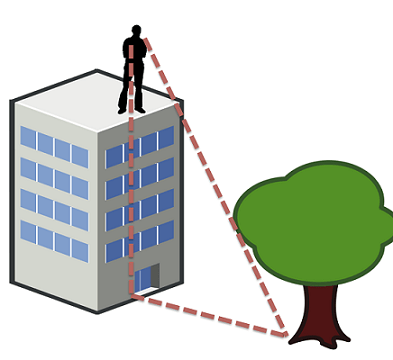
29. Show or sketch Figure 5 to illustrate to students how right triangles can be employed in this new situation.
30. Have students form into small groups and in each group have one student stand on a chair and point to an object (such as another chair) using his/her arm to form a 45-degree triangle.
31. Then have students use protractors to better estimate the same 45-degree angle. This is the angle formed by pointing the movable arm of the protractor towards the object.
32. In order to find their height above the ground, direct one student to use the LEGO intelligent brick with the LEGO ultrasonic sensor attached. Do this by pointing the ultrasonic sensor at the ground and reading the value displayed on the LCD screen of the brick running the "View" program. (Note: No separate program is needed to do this; just use the built-in sensor viewing capability of the EV3 brick. Find this built-in program by going to the main menu > selecting the "View" option > selecting the "Reflected Light" option > selecting the port that the color sensor is connected to.)
33. When students use the LEGO brick in this way, they are using modern technology to measure distances just like engineers on construction sites. Using the information gathered, which is the angle and height, students can estimate the distance along the floor to their objects. This is the distance from their position on the chair to the object being viewed.
34. Finally, have students compare the actual distance (measured with rulers) to their estimates, recording their results on their worksheets. Have each student in each group do this.
35. Evaluation: Next, have students compare the accuracy of their results in measuring the height of the ceiling in the classroom.
36. While standing flush with a wall, direct students in each group to use the LEGO brick with ultrasonic sensor to measure the distance from their shoulders to the ceiling as well as from their shoulders to the ground.
37. By adding these two values from the sensor, students obtain the height of the classroom.
38. Next, have students compare these values with the prior results obtained by estimation during the application subsection of the activity.
39. Finally, provide students with the actual ceiling height so they can compare that value with their estimates.
40. Lead a class discussion to share and compare results and conclusions.
41. Collect the completed worksheets for grading.
42. Administer the post-activity assessment (same as pre-activity assessment).

Vocabulary/Definitions

cubit: An ancient Egyptian standardized measurement unit equal to the length of the arm of a royal master from the elbow to the end of the fingers (~18 inches or 46 cm).

equilateral triangle: A triangle in which all three sides are the same length, resulting in each of its angles being 60°.

estimation: The process by which we take an educated guess as to what the real value of an object is, without measuring the exact value.

isosceles triangle: A triangle with two equal sides, resulting in two angles being the same.

right triangle: A triangle that has one angle equal to 90°; its sides are called the hypotenuse (longest side), base and height. Also called a 45° right triangle or a 45-45-90 triangle.

scalene triangle: A triangle with sides of three different lengths resulting in all three angles of being different.

Assessment

Pre-Activity Assessment

Before beginning the activity, administer the seven-question Triangles Activity Assessment to give students a chance to think about questions that will be answered during the activity, and gauge their baseline understanding of the subject matter.

Activity-Embedded Assessment

During the activity, have students complete the Triangles Activity Worksheet with recorded observations, measurements and reflections. Observe students' worksheets during the activity. Collect the worksheets at activity end to assess students' progress during the activity.

Post-Activity Assessment

After the activity, administer the same Triangles Activity Assessment again to determine student comprehension and skill enhancement.

Investigating Questions

What is a triangle? (Answer: A triangle is a closed, three-sided figure or polygon.)

How can we estimate the height of a building? (Answer: By using a right triangle and knowing our distance from that building.)

What is special about a 45-degree right triangle? (Answer: This type of triangle has a base length equal to its height.)

Activity Scaling

• For lower grades, begin the activity by considering a square and asking: What makes a square a square? Through illustrations, teach students that a square has four sides all of which have the same length and the adjoining sides of a square all form 90° angles. Next, ask students to examine the resulting shape when a square is sliced in half by a diagonal line. Ask students to name the kind of triangles formed. Lead them to notice that the resulting triangles have two equal-length sides that form right angles. Explain that they can use the length of one side of a right-angle triangle to estimate the length of the other (equal-length) side. Have students practice estimating a 45° angle by using their arms. For example, in the application phase, when measuring the classroom ceiling height, have elementary school students move about in the classroom holding out their arm at approximately 45° angles instead of using protractors.
• For upper grades, after the Introduction/Motivation review of all trigonometry concepts, including the use of protractors, explain the basics of sine and cosine functions and how they relate to right-angle triangles. Ask students to investigate how the knowledge of the length of the base of the triangle along with the angle formed with the hypotenuse constitutes sufficient information to calculate the height of the opposite side of the triangle. For example, in the application phase, when measuring the classroom ceiling height, instead of a 45° angle, ask students to use a different angle and follow the same procedure as above with a protractor. Finally, ask students to measure the angle formed by the known side of a right-angle triangle and its hypotenuse.

References

Copyright

Contributors

Supporting Program

Acknowledgements

This activity was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.