Lesson Navigating by the Numbers

Learning Objectives

After this lesson, students should be able to:

• Describe how navigation and engineering are based on mathematics
• Describe how the Pythagorean Theorem solves real-world problems.
• Explain the difference between accuracy and precision

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Introduction/Motivation

How important is math in navigation? (Possible answer: It depends on the goal of the traveler.) If you have unlimited time and your destination is visible from miles away, you may not need math. But if you want to get somewhere as fast as possible or the destination is not visible until you are on top of it, math is an essential component to get you where you're going. Engineering is another important factor in navigational technology. Imagine how navigation allows us to explore unknown (or known) territories with a small, portable device that works almost everywhere — we can thank engineers for the amazing technology.

You can navigate to your home without doing any math because there are visual clues to guide you. You can even drive from one city to another, and within a new city, without math because signs have been put up to direct drivers. On the other hand, if you try to cross an ocean where there are no landmarks, you could not navigate accurately without math. For the Polynesians crossing the Pacific Ocean, approximate methods worked because they could use visual clues (such as birds, waves, stars) once they were within 100 miles or so of their destination. Even then, however, they had to imagine angles, count multiples of the distances between stars, and visualize vectors of wind and water currents. Essentially, these early Polynesian sailors were doing geometry in their heads.

As the world grows more complex and engineering provides new technologies, we want to navigate faster and know exact distances and times of travel. How did people first determine distances between cities? Or, how about the size of the Earth? (Answer: They measured the distance between two cities and then used trigonometry to extrapolate that to the size of the Earth.) Is it possible to determine the width of a river without crossing it? (Answer: Yes, but it requires that you understand, and use, trigonometry.)

This is all possible using relationships of simple shapes and angles. These principles can be applied to determine almost any distance or height given appropriate reference points. At the heart of both navigation and engineering is the art and science of measuring on, near, or beneath the surface of the Earth — known as surveying. Surveyors are able to determine very exact relative distances and heights, and this allows precise positioning of anything being built, greatly improving strength, accuracy, and even the safety of the final product. A survey engineer is needed in many career areas, including: the forest service, city and road planning, building construction, cartography (map making), mining, and even building satellites.

Lesson Background and Concepts for Teachers

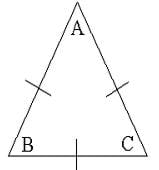
The sum of the angles in any triangle is always 180°.

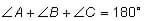
Types of triangles:

Pythagorean theorem was an idea discovered by Pythagoras, a Greek mathematician who lived from 569-500 B.C. It is said that he discovered the special property of right-angled triangles while looking at the tiles of an Egyptian Palace. Pythagoras said, "In a right-angled triangle, the area of the square on the hypotenuse equals the sum of the squares on the other two sides."

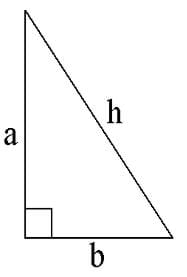
h is the hypotenuse

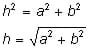
A radian is the angle made when the radius of a circle represents an arc on its perimeter.

One radian is the measure of the angle created at the center of a circle by an arc on the perimeter equal in length to the radius of the circle. Students can relate this measurment to the real world association of measuring the arc length of distance travelled on earth in the associated activity Stay in Shape.  A radian is a different way to measure an angle than using degrees.

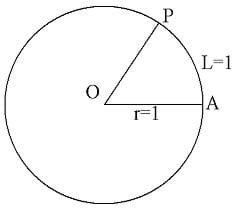
and length, L = 1 unit

then ∠AOP = 1 radian

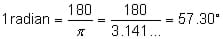
1 radian = 57.30 degrees

If there are 360º in a circle, then 360º / 57.3º per radian = 6.28 radians on the perimeter of a circle. Notice that number equals 2 x 3.14 (pi or π) radians; therefore, 3.14 radians = 180º.

See more descriptions and sample problems at the following website: http://www.staff.vu.edu.au/mcaonline/units/trig/trigraddegrees.html

Trigonometry

Trigonometry is a branch of mathematics dealing with relationships of the angles and sides of triangles. The three basic trigonometric relations that we are concerned with — sine, cosine and tangent — are ratios of the lengths of two sides of a particular triangle. A very useful type of triangle is a right triangle, which has one angle equal to 90º. By definition, the 90° angle is made by two lines that are perpendicular to each other (like the corner of a square), and the third side of the triangle is made by a sloping line connecting the two perpendiculars. This sloping line is called the hypotenuse, and the name comes from the Greek words hypo (meaning under) and teinein (meaning to stretch). Essentially, hypotenuse means to stretch under the 90º angle. It is easiest to show this visually.

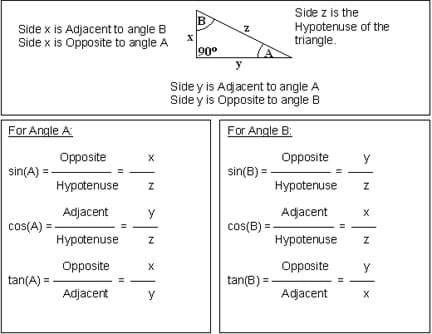
The letters SOH CAH TOA can effectively help students remember which sides go with which functions (Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, etc.). Mnemonics may help students memorize the relations: "Some Old Hag Caught A Hippie Tripping On Art" or "Some Oaf Happily Cut A Hole Through Our Apartment". Students can relate trigonometry to real world engineering applications such as basic surveying with the fun associated activity Trig River.

Associated Activities

• Stay in Shape - Students learn how distances on the surface of the Earth are arcs, and not straight lines. They also learn how to calculate the arc length. The come to understand why knowing about geometric shapes such as triangles and circles is fundamental to understanding navigation.

  Watch this activity on YouTube

• Trig River - Students act as engineers and use trigonometry to learn basic surveying. They also learn how to determine the width of a "river" without actually crossing it!

  Watch this activity on YouTube

Lesson Closure

Without knowledge and use of math at some level, most navigation, and engineering, is random wandering and luck. Even using the sun as a guidepoint means you use geometry: You must have a mental picture of a plane (the Earth), a reference point (the sun), and the angle away from the reference point toward your destination. Understanding the mathematical relationships of shapes, angles, and the physical universe allows navigation to become efficient and safe rather than just hoping to reach a destination. Even the simplest equation, speed x time = distance, can be a mental guess (say roughly 20mph x about ¾ hour = 15 miles) or a precise calculation (21.3257mph x 44.3552 hours = 15.7651 miles). Whether the goal is finding a continent across an ocean or determining a satellite orbit to within centimeters, engineering and math can get you there.

Vocabulary/Definitions

geometry: The mathematical relationships of points, lines, angles, surfaces and solids.

trigonometry: The mathematical relationships between the sides and the angles of triangles.

Assessment

Pre-Lesson Assessment

Discussion Question: Solicit, integrate and summarize student responses.

• How important is math in navigation? (Answer: It depends on the goal of the traveler. If you have unlimited time and your destination is visible from miles away, you may not need math. But, if you want to get somewhere as fast as possible or the destination is not visible until you are practically on top of it, then math is essential.)

Post-Introduction Assessment

Voting: Ask true/false questions and have students vote by holding thumbs up for true and thumbs down for false. Tally the votes, and write the totals on the board. Give the right answer.

• Thumbs Up: if you think it is good to use math when navigating.
• Thumbs Down: if you think navigation can be close enough without math.
• Thumbs Up: if you think math is important for engineers to know how to use.

Lesson Summary Assessment

Student-Generated Questions: Solicit, integrate and summarize student responses.

• Have students come up with one question of their own to ask the rest of the class. Be prepared to provide help to some students form questions. Have students take turns asking their questions to the class for as long as time permits.

Lesson Extension Activities

Use the latitude and longitude of two cities on the globe to find how far apart they are: http://jan.ucc.nau.edu/~cvm/latlongdist.php  

Estimate the size of the Earth: Use the following link, http://jan.ucc.nau.edu/~cvm/latlongdist.php, to find the distance between two cities that are on the same longitude line. By knowing the difference in latitude between the cities and that the circumference of the Earth has 360º of latitude, the students should be able to come up with an estimate of the Earth's circumference. (Answer: Divide the distance between cities by the difference in latitude (degrees) so that the distance per degrees of latitude is known. 360º multiplied by this distance/º should give a number very close to the circumference of the Earth at the equator. (Answer: About 24,900 miles or 40,070 km.)

Have students research other methods of determining the circumference or radius of the Earth. Eratosthenes (276-194 BC) was a Greek scholar who was the first person to determine the circumference of the Earth. Many additional methods have been found since the hard work of Eratosthenes.

References

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.