Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00
Group Size: 1
Activity Dependency: None
Subject Areas: Earth and Space, Geometry, Measurement
Summary
Accuracy of measurement in navigation depends very much on the situation. If a sailor's target is an island 200 km wide, sailing off center by 10 or 20 km is not a major problem. But, if the island were only 1 km wide, it would be missed if off just the smallest bit. Many of the measurements made while navigating involve angles, and a small error in the angle can translate to a much larger error in position when traveling long distances.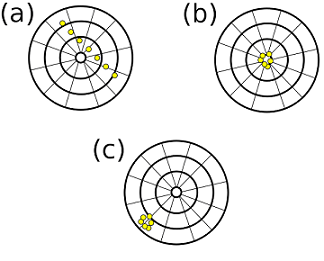
Engineering Connection
One of the most useful tools in engineering is the computer. Some engineering mathematics are so complicated that problems would be impossible to solve without a computer. Computers help engineers determine how accurate and precise something must be to work correctly; engineers can save time and costs by avoiding over-designing systems to be more accurate and precise than necessary.
Learning Objectives
After this activity, students should be able to:
- Understand the difference between accuracy, precision, and error.
- Recognize basic trigonometric functions and analyze functional relationships.
- Understand that math is fundamental to navigation
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Explain and use the relationship between the sine and cosine of complementary angles.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
(+) Understand and apply the Law of Sines and the Law of Cosines to find unknown measurements in right and non-right triangles (e.g., surveying problems, resultant forces).
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Represent and analyze quantitative relationships between dependent and independent variables.
(Grade
6)
More Details
Do you agree with this alignment?
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Define trigonometric ratios and solve problems involving right triangles.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Describe methods and equipment used to explore the solar system and beyond
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each student (or team) needs:
- A computer with Microsoft Office Excel® installed
- A copy of the Computer Accuracy Excel file loaded on their computer
- A copy of the Computer Accuracy Worksheet
- Pencil
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_navigation_lesson04_activity2] to print or download.Introduction/Motivation
When we sent astronauts to the moon, do you think it mattered if they were off by 1 degree? (If you have a protacotor, hold it up in front of the students.) How about if they were off by 1/10th of a degree? Would they still make it? Should we worry if they are off by 1/1000th of a degree? (Answer: It depends on the mission requirements, but have students keep these thoughts in mind during the activity.) These and other questions can be answsered by understanding, and doing, math while navigating.
Procedure
Accuracy and Precision in Measurement
There are two basic concepts to any collection of measurements, accuracy and precision. Accuracy is how close the measured data is to the actual value. For example, if you know that you have a mass standard that is 50.00 grams, and you measure it to be 49.98 grams, then your measurement is very accurate. On the other hand, if you measure it to be 43.24 grams, your measurement is not very accurate.
Precision is how close your measurements are relative to each other, not the actual value. For example, let say you measured that same mass standard and came up with the values:
43.24, 43.30, 43.20, 43.25, 43.32
You could say that your measurement was very precise because all the values are very close to each other. On the other hand, if your measurements were:
50.03, 43.40, 53.01, 47.54, 30.23
Your measurements would not be very precise because they are all far apart relative to each other.
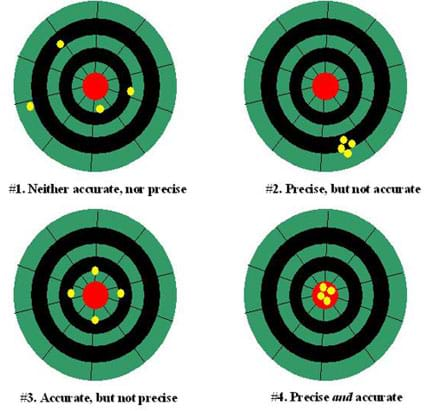
A dartboard is a common example of showing the difference between accuracy and precision (please see Figure 1). Assume that someone throws four darts at a dartboard. If they are far apart and unevenly spaced, they have neither precision nor accuracy (#1). The closer the darts are to the center, the better accuracy they have. The closer the grouping of darts is to one another, the better precision they have (#2). If the darts are evenly spread around the center, the dart thrower has low precision but high accuracy — they are not close to each other but all of the darts are equally far from the center (#3). And finally, if all of the darts are closely grouped in the center of the dartboard, the thrower has both high accuracy and precision (#4) because the darts are either on or very close to the target.
Trigonometry
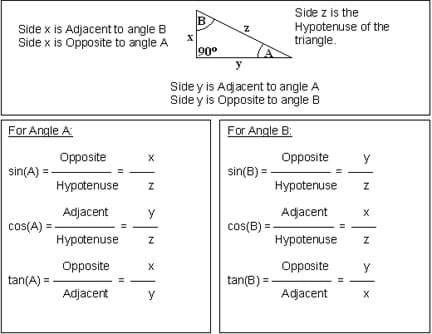
Trigonometry is a branch of mathematics dealing with relationships of the angles and sides of triangles. The three basic trigonometric relations that we are concerned with — sine, cosine and tangent — are ratios of the lengths of two sides of a particular triangle. A very useful type of triangle is a right triangle, which has one angle equal to 90º. By definition, the 90° angle is made by two lines that are perpendicular to each other (like the corner of a square), and the third side of the triangle is made by a sloping line connecting the two perpendiculars. This sloping line is called the hypotenuse, and the name comes from the Greek words hypo (meaning under) and teinein (meaning to stretch). Essentially, hypotenuse means to stretch under the 90° angle. It is easiest to show this visually.
Before the Activity
- Perform a trial-run of the activity beforehand.
- Print out enough Computer Accuracy Worksheets for each individual or group.
- The MS Excel® files are write-protected against changes (with the exception of the data entry boxes), but the protection can be removed, if necessary. If students are fairly computer savvy, a password may be added to further guard against file corruption (but, if you are going to do this, make the change and save the file before loading onto each student computer). To add a password to the file, the following instructions are provided:
- On the Tools menu, point to Protection, and then click Unprotect Sheet.
- Then again, from the Tools menu, point to Protection, and then click Protect Sheet.
- When prompted, leave all boxes checked and enter a desired protection password for the worksheet. Passwords are case sensitive. To unprotect the sheet again, you must type the password exactly as it was created, including uppercase and lowercase letters.
- Load the Computer Accuracy Excel file onto all computers to be used and put it in an easy to access place (the Desktop, for instance) or have the file opened up when students arrive to class.
- MAKE SURE to start the students on the Excel file with answers that are incorrect! If necessary, input "10" into all of the yellow boxes before the students arrive.
With the Students
Before students sit at computers:
- Ask students a discussion question to get them thinking about the topic. (Hold up protractor if you have one.) When we sent astronauts to the moon, do you think it mattered if they were off by 1 degree? How about if they were off by 1/10th of a degree? Would they still make it? Should we worry if they are off by 1/1000th of a degree? (Answer: It depends on the mission requirements, but have students keep these thoughts in mind during the activity.)
- Divide the class into groups (if enough computers available) and give each student or group a Computer Accuracy Worksheet.
- Discuss the concepts of the "Sail to an Island Harbor" problem in terms of the increased accuracy needed compared to just finding the island. Remind the students that they know the exact measurements from their ship to the center of the island. However, they do not want to simply reach the center of the island, they want to find the harbor. Students will need to adjust the angle so that they are 1 km north of the island. This will allow the ship to get close enough to the harbor to see it with the naked eye if they are slightly off. What happens if it is foggy outside? The ship now needs to be within 100m (0.1 km) of the island to be able to see it. How accurate does the new angle need to be?
- Discuss the concepts of the "Rocket to a Moon Orbit." This problem shows how the error in the navigation measurement of the initial angle can greatly affect the final destination. Remind students that they will run this experiment twice. Once with an accuracy error of ± 0.1°, and again with an accuracy error of ± 0.01°. (A new angle of around 37.38° will work well. Students will not be able to launch successfully with an error of ± 0.1° because all three outcomes are possible with the given error).
At the Computers:
- Have students do the "Sail to an Island Harbor" problem and come up with creative things to search for on the mystery island.
- Have students do the "Rocket to a Moon Orbit" problem and answer the questions at the bottom of the Worksheet.
- Each group or individual should print out the Excel file with the correct angles (assuming printers are available – otherwise students could write their numbers on the worksheet).
- Work the problem equations backward to find the needed angles without all the guess work. This will require using the "arcsin" or "inverse sin" function on a calculator. Is it faster to solve the equations backward or guess on the computer?
Assessment
Pre-Activity Assessment
Discussion Questions: Solicit, integrate and summarize student responses.
- (Hold up protractor if you have one.) When we sent astronauts to the moon, do you think it mattered if they were off by 1 degree? How about if they were off by 1/10th of a degree? Would they still make it? Should we worry if they are off by 1/1000th of a degree? (Answer: It depends on the mission requirements, but have students keep these thoughts in mind during the activity.)
Activity Embedded Assessment
Worksheet/Computer Calculations: Have the students complete the worksheet; review their answers to gauge their mastery of the subject.
- Students follow and complete the attached Excel® file and worksheet.
Post-Activity Assessment
Student Generated Questions: Solicit, integrate and summarize student responses.
- Have students come up with one (or more) question of their own to ask the rest of the class. Be prepared to help some students form a question. Have students take turns asking the class their question.
Troubleshooting Tips
These worksheets could be confusing if not explained thoroughly from the start. Remind students that in the case of both the ship and the rocket, there are known distances and angles and they have to make corrections to them to reach a target (harbor or orbit).
Activity Extensions
Have students go to: http://www.staff.vu.edu.au/mcaonline/units/trig/ratios.html to investigate a navigation example using trigonometry.
Have the students find the largest accuracy error that still allows a safe launch (i.e., the rocket arrives at exactly 2000 km and has +/- error equal to 99 km).
Activity Scaling
- For lower grades, eliminate step #4 (of "At the Computers") in the With the Students section.
- For upper grades, have students do the "Sail to an Island Harbor" problem by hand first (give them a first guess of 37.1º and tell them they should try to get an opposite side length within 0.1 km of 602.8) and then check their answer with the Excel® file. Hopefully, they will only have to do the calculations three times: 37.1 (see, it needs to be smaller), or 37.05 (it needs to be bigger) and then, 37.075 (bingo!).
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students investigate error in the context of navigation because without an understanding of how errors can affect your position, you cannot navigate well. Introducing accuracy and precision develops these concepts further. Also, students learn how computers can help in navigation.

Students use right triangle trigonometry and angle measurements to calculate distances using accuracy and precision. They understand the relationship between triangulation technology and other fields of study (i.e. mathematics).

Students learn that navigational techniques change when people travel to different places — land, sea, air and space. For example, an explorer traveling by land uses different navigation methods and tools than a sailor or an astronaut.
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Jeff White; Matt Lippis; Penny Axelrad; Malinda Schaefer Zarske; Janet YowellSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326.
Last modified: October 7, 2022








User Comments & Tips