Hands-on Activity Sextant Solutions

Learning Objectives

After this activity, students should be able to:

• Use trigonometric functions to determine angle measurements.
• Analyze functional relationships and examine how a change in one variable results to change in another.
• Explain the connection between computer technology and navigation
• Explain how advancements in technology have improved humans' ability to navigate

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

Each student (or group) needs:

• computer with Microsoft Office® Excel® installed
• Sextant Corrections Excel® File, loaded on the computer
• Sextant Corrections Worksheet, one per student or one per group; if working in groups, the teacher determines whether each student gets a worksheet to complete or if students complete one worksheet per group
• pencil
• calculator

Worksheets and Attachments

Introduction/Motivation

(Continuing with the concept of trying to measure small angles accurately, introduce the sextant and discuss it with the class.)

What is sextant? (Answer: A tool developed by early navigators to determine latitude and longitude.) Instead of naviagators trying to line up a separate horizon line and sun line (to determine one's location), the sextant allowed the two images to be moved together—greatly increasing the accuracy of the angle measured.

Why would measuring a precise angle be important? (Answer: By knowing this angle and your local time, your latitude can be determined. If you also know the Greenwich Mean Time [GMT], your longitude can also be determined.)

What happens if the angle is measure incorrectly? (Answer: It will likely affect what you think is your current location.) Computers can help ensure that angles are correctly measured. When higher accuracy is needed, calculations become more difficult so using computers is even more practical. Computers allow you to try many numbers in an equation quickly—giving the operator a better chance to understand what the equation represents.

Procedure

A sextant's accuracy is expressed in "seconds of arc." A degree is divided into 60 minutes (noted as 60') and a minute is divided into 60 seconds (noted as 60''). A good thing to remember is that each minute of angular measurement represents a distance of 1 nautical mile. A sextant scale can generally read out to one-fifth or one-tenth of a minute—quite an accurate reading. But, that reading is not the final accuracy, as several corrections must be made to that angle. At this point, the navigator must perform what amounts to a full page of corrections and calculations using astronomical tables and charts. The accuracy of the correction values affects the final result and the calculations offer ample opportunity for human error.

Depending on the accuracy of the corrections, the final angular measurement could easily be off by several minutes or more, so most navigators (assuming they are skilled and have good weather) expect at best an accuracy of within a few miles.

Today, refined manufacturing techniques and robust materials make sextants last longer but do not improve the accuracy of the tool, which is limited by the fuzzy edges of celestial objects. Skill in use and better understanding of the math and geometry involved can improve accuracy slightly (compared to the past). But, a large chance of error still exists in the doing many pages of calculations needed! This is where a modern advantage comes in—the computer.

When used correctly by an experienced navigator and under ideal weather conditions, a well-made sextant can measure an angle with precision to the nearest 10 seconds of arc (10 seconds of a degree is about 0.003 degrees of a 360-degree circle!). A computer can do the corrections and calculations quickly, and an accuracy of 0.2 miles in final position is possible. More likely, it will be about twice that under normal weather conditions (0.4 miles), and in poor conditions, it may still be 1-2 miles off. This is no better than measurements taken in good weather conditions hundreds of years ago, but thanks to the computer, navigators no longer have to do all the math by hand.

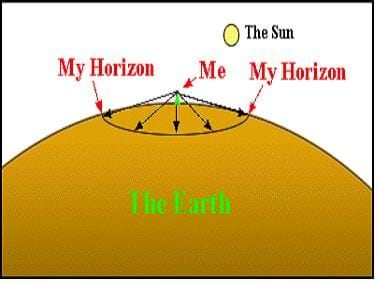
Sextant Use and Error

The sextant is a high-precision instrument. Caution must be used when handling a sextant since even mild shaking might cause damage. The movable arm has an arc range of 60°, and this is why it is called a sextant. You double this measurement to 120° to find your altitude angle. Every sextant has an inherent error called its offset. Sextants can be calibrated to determine their offset. Once the offset is known, you correct for the error in the sextant calculations.

Besides the sextant offset, many other sources of error exist. In this activity, we will look at two sources of error when using a sextant.

1. Looking at Figure 1, the person who looks at the horizon is not looking straight, but down a bit. This is because the Earth is round, not flat. The angle that you look down depends on how tall you are. If you are on top of a building that is in the middle of a big field, you have to look down quite a bit to see the horizon. If you are lying on your stomach in the field, you do not have to look down at all (this is illustrated in the Sextant Corrections Worksheet). It is easier to use a sextant when you are standing, so the angle that you are measuring is actually larger than the true altitude. This error is called the "dip of the sea horizon." Luckily, it is easy to figure out using the following equation:

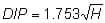
H is the height of your eye in meters and DIP is the correction in minutes of arc. Subtract this from the angle you measure using the sextant.

2. Another source of error is the refraction effect of the atmosphere. The Earth's atmosphere bends the light coming from the sun. The sun might be below the horizon, but the atmosphere bends the sunlight so that you still see it. Just like the DIP, this makes the altitude seem larger than it is. The amount of bending depends on the atmospheric pressure, the temperature and your altitude. A good approximation for this error is:

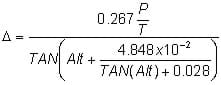
The triangle is called delta and is in minutes of arc

P is the atmospheric pressure in millibars (1 atm = 1,013 millibars)

T is the temperature in °Kelvin

Alt is the altitude in degrees (reading from the sextant corrected for dip)

Before the Activity

1. Make copies of the Sextant Corrections Worksheet, one per group or one per student.
2. The MS Excel® files are write-protected against changes (with the exception of the data entry boxes), but the protection can be removed, if necessary. If students are computer savvy, add a password to guard against file corruption (but, if you are going to do this, make the change and save the file before loading onto each computer). Follow these steps to add a password to the file:

• On the Tools menu, point to Protection, and then click Unprotect Sheet.
• Then again, from the Tools menu, point to Protection, and then click Protect Sheet.
• When prompted, leave all boxes checked and enter a desired protection password for the worksheet. Passwords are case sensitive. To unprotect the sheet again, type the password exactly as it was created, including uppercase and lowercase letters.

3. Load the Sextant Corrections Excel® File onto all computers and put it in an easy-to-find location (such as on the computer desktop), or better yet, have the spreadsheets open when students arrive.

Note: In the "Refraction of the Atmosphere" section, the Temperature and Pressure data boxes are not protected. This is to enable the option of investigating these variables, but they are not highlighted to keep the basic lesson more focused. See Activity Scaling section.

With the Students

Before students go to the computers:

1. Divide the class into groups (depending on the number of computers available) and give each student or group a worksheet.
2. Discuss the concepts of the "Dip of the Sea" correction. If students have calculators, have them check the 2-meter height example answer.
3. Discuss the concepts of the "Refraction of the Atmosphere" correction. Reassure them they will NOT have to do this calculation by hand. Emphasize that the computer will be doing that calculation every time they put in a new number. This enables students to experiment and try many angles and look for trends in the results.

At the Computers:

1. Have students do the "Dip of the Sea" correction and answer the worksheet questions.
2. Have students do the "Refraction of the Atmosphere" correction and answer the questions at the bottom of the worksheet.
3. Have each group or individual turn in the completed worksheet; no print out is needed.
4. Try doing the Refraction example equation. The 10 °C temperature must be converted to Kelvin (283.15 °K) when used in the equation, and all other values are as shown. Note the results are given in minutes of arc, and 1 degree has 60 minutes of arc.

Assessment

Pre-Activity Assessment

Discussion Questions: Solicit, integrate and summarize student responses.

• Who would believe me if I told you that when you are looking at a sunset, the sun has actually already set? Encourage discussion: How much can we trust our eyes? Is the sun setting or are we? How could the sun have already set if we can still see it? (Answer: It is a true statement because the Earth's atmosphere refracts [bends] the rays of sunlight over the horizon, allowing us to still see the rays for a while after the sun has geometrically set!)

Activity Embedded Assessment

Worksheet/Computer Calculations: Have student follow and complete the Sextant Corrections Worksheet and Sextant Corrections Excel® File. Review their answers to gauge their mastery of the subject.

Post-Activity Assessment

Questions/Answers: Ask the students and discuss as a class:

• Would someone using a sextant on the moon need to make these same corrections? Why or why not? How might they be different? (Answer: The horizon dip effect would still need to be corrected on the moon and it would be larger because the moon is smaller than Earth; therefore, its horizon "dips" away even faster than Earth's. Imagine standing on a basketball! Looking down, you can see almost 90 degrees around the horizon of the ball. This is a HUGE dip error. The refraction of the atmosphere correction would not be needed since the moon has almost no atmosphere.)

Activity Scaling

• For younger students, have them help each other and do one worksheet per group. Also, do not have students complete Step #4 (of "At the Computers") in the Procedure > With the Students section.
• For more advanced students, let them vary the temperature and atmosphere values for the refraction correction. A normal range is -15 °C to 40 °C, and 970 mbar to 1030 mbar. Collecting and plotting this data is a good way to see which affects the equation the most. Challenge students to determine why these values increase or decrease the refraction. (Answer: Cold air is denser than hot air and high-pressure air is denser than low-pressure air; therefore, a denser atmosphere creates more refraction.)

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under grants from the Satellite Division of the Institute of Navigation (www.ion.org) and the National Science Foundation (GK-12 grant no. 0338326). However, these contents do not necessarily represent the policies of the National Science Foundation and you should not assume endorsement by the federal government.