Lesson Projections and Coordinates:
Turning a 3D Earth into Flatlands

Learning Objectives

After this lesson, students should be able to:

• Describe the true shape of the Earth, that it is more than simply "round."
• Explain the difficulty of trying to make a rounded object exist in a flat map space.
• Articulate the reality that all flat maps of the globe are flawed in some way and be able to discern what those compromises might be. Be able to list common ways in which maps alter reality in their representation of space.
• Identify the important components of any geographic coordinate system—a value for every spatial dimension, a designation that is unique to every location within the system.
• Explain that coordinate systems are just designed systems. Any number of coordinate systems can be generated or used, though they have various strengths and weaknesses.
• Explain how latitude and longitude relate to the curved Earth surface as angles.
• Explain how engineers apply coordinate systems to map various surfaces.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

International Technology and Engineering Educators Association - Technology

State Standards

Worksheets and Attachments

Introduction/Motivation

The True Shape of the Earth

What shape is the Earth? Is it flat, a cube, a football, a sphere? For whatever answer you think, how do you know that it is that shape? Are you sure that the Earth isn't flat? Did Columbus really prove that? If the Earth is round, then show me. Can you show me that Earth is round by looking out the window? What if we went to a tall building nearby? Would I be able to see that the Earth is round as you say if I went to a 100-story building? How about a 150-story building? Would it take going up high on an airplane to see the Earth's curve? In fact, if you go to a tall building or into an airplane, you will not see the Earth curve in any way. Why is that? The reason that is, assuming that the Earth is round, is that we are very small on the surface compared to whole size of Earth. Can you imagine being small enough to fit on this little spot (use an orange or a globe to illustrate with a real physical object)? Would you see the Earth curve then? You're right that you probably would not.

What about maps? Are maps flat or round? Have you ever seen a round map? (If no one answers "yes," then point out that a globe is a round map.) No one said that maps must be round, but why are so many maps round? Is it just because it is too hard to make little curved surfaces for people to carry around? Maybe it would simply be too hard to fold up a rigid curve and put it in your pocket? Well, using what we were just saying about being able to see the Earth's curves while standing on Earth, how different would a curved map of our city look from a flat map of our city? How much curve would you even see in the map if you cannot see the Earth's curve while you are walking on it? In fact, you might not be able to tell much difference at all. In the same way that the Earth's surface curves compared to our scales, a map of a city-sized area or smaller behaves similarly.

Returning back to the shape of the Earth, we are agreeing that the Earth is "round" in some way and has curves. But which one of these shapes is it really? (Show an image of different types of sports balls.) Is it a sphere, more like a football, or maybe even a golf ball? What if I told you that the Earth is not a sphere at all? Would you believe me? Who told you it was a sphere? Just because the Earth is round, does that mean that it "has to" be a sphere? In fact the Earth is NOT a sphere at all. It is closer to a sphere than a flat disk, but an even better approximation for the shape of the Earth is an ellipsoid. (Go on to explain what an ellipsoid is. Note the reason that the main difference is a "bulge" at the equator and outline the rotational causes for the bulge.) So are you confused yet? Well prepare to be confused again because the Earth is not really an ellipsoid either, but rather what we call a geoid (pronounced GEE-oid).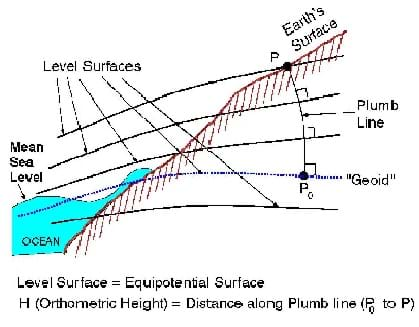

A geoid is "the equipotential surface of the Earth's gravity field that best fits, in a least squares sense, global mean sea level." [1] This a way of saying that there is a surface of equal gravity that would coincide with the real water level of the entire world's oceans if they suddenly stopped moving. The geoid is not something that you can "see" in a normal sense. It is based on a gravity field. So why does it vary? (Point to an illustration of the geoid.) Yes it's true that the Earth's surface varies because of natural topography—the rise and fall of the land. Mountains exist underwater and on continents, but this is not what we're actually talking about. The geoid varies because gravity pulls on different objects to different degrees depending on their masses. Which is heavier, dirt or water? Dirt is generally heavier or denser because it sinks in water. So one of the reasons that the geoid varies as you see is that soils and water are not distributed evenly on the Earth's surface. The different types of materials that exist below the Earth's surface do not necessarily distribute evenly either. This creates the effect of a varying gravity surface that gives us the geoid. [2]

Projections

So why does it matter if we know the shape of the Earth? Scientists and engineers created flat maps because they are much easier to read and use for navigation. In order to create an accurate map, the true shape of the Earth matters because we have to project it in some way. Hence what is called a projection. When you project a 3D object to a 2D surface, you create some inaccuracies. It is better to start with a model of the Earth that is more correct before you introduce more inaccuracies. So a geoid model or even a simple ellipsoid is better for making a map than a true sphere.

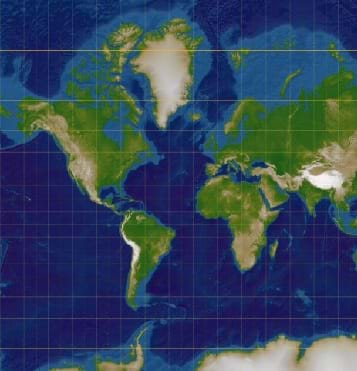
Let's examine the inaccuracies that might occur when you project the Earth to flat space. (At this point, unpeel an orange to demonstrate what happens when you break open a round object and flatten it. First, draw "continents" on an orange, then peel the orange in one continuous peel. When you flatten the peel on a piece of paper, it becomes clear how the Earth's surface must be broken in some way to make possible any kind of flat map projection.) Now let's examine some different projections that people use. Take the Mercator projection. It is one of the very oldest (est. 1569), but it misrepresents the true Earth in some ways. Can you see the errors in the map? One obvious distortion is what happens with the island of Greenland. Look at Greenland and notice how big it appears compared to the African continent. It appears to be about the same size, but in reality Greenland is 14 times SMALLER than Africa. This projection is made by imagining the Earth as if it were inside a can. You roll the Earth onto the inside of the can and then unroll the can. What you have in the end are land masses in the middle of the Earth that are fairly close to accurate (such as Africa, China, the US), but the land masses closer to the poles are expanded vertically to reflect more land than is really there. The same is true for extremely northern and southern oceans. (Conduct a similar discussion for the Albers Conic Equal Area projection. Note that Greenland and Africa are the correct size in this projection, but their shapes are now distorted.)

Coordinates

So consider what would happen if you went to the North Pole. What would it look like there? So what if you knew that you were right on the exact spot that was the North Pole? If you step backward, what direction are you moving? What about if you step left or right? Any direction that you move from that position is south. There is no other way to go because you are at the point on the Earth that defines what we call north. Of course, a compass would not work correctly at this location because a compass generally uses magnetic north, which in this instance is not the same as true north. So how good would a standard "compass rose style" map do you in this situation? It wouldn't do you very well because all of your coordinates are based on using the cardinal directions. In reality, navigators, cartographers, petroleum geologists and all those that have an interest in going to the North Pole generally do not use the standard latitude and longitude spherical coordinate system. They use an alternative system called Universal Polar Stereographic (UPS) that divides the North and South Pole into a more useful flat surface grid at these extreme locations. Students can expand their knowledge of coordinate systems with the associated activity Who Can Make the Best Coordinate System? where they make their own coordinate systems using a common area across all groups and compete to see who can make the best one.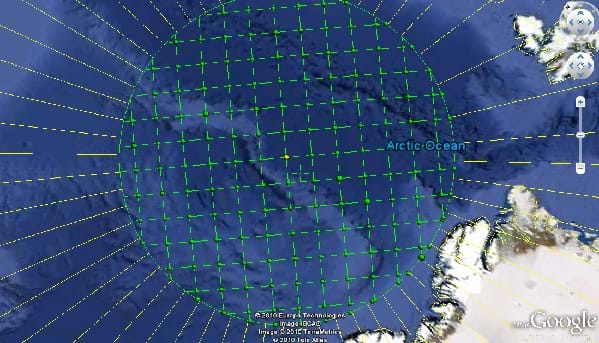

Let's look at another example of coordinates so we can see what makes something a coordinate system and why a coordinate system is something significant. Perhaps someone has played the classic Milton Bradley game, Battleship. If you look at a map of Battleship (grid of lettered rows and numbered columns), can you describe any location on the map? Yes you can. We use two dimensions and two coordinates to describe those dimensions. This is a very simple and useful type of map in some situations. It requires almost no explanation. (Further discussion can be generated on this topic using the Who Can Make the Best Coordinate System? activity.)

Now examine two common coordinate systems. The first is standard latitude-longitude and the second is called Universal Trans Mercator (UTM). Latitude-longitude actually measures angles, which is why it is given in units of degrees, from the centerlines of the Earth, either the Prime Meridian or the Equator.Note that the Prime Meridian, unlike the Equator, is arbitrarily chosen to go through Grenwich, UK. It just as easily could have gone through Bangkok, Moscow, or Chicago. This is one aspect of this coordinate system that is based on a convention that was chosen. The Equator makes a little more logical sense because it is the north-south middle line between the poles. Notice that the lines of this coordinate system curve to follow the Earth's surface and that for the case of longitude, they all meet as one at the poles. This meeting is part of the reason why the UPS system is a more useful coordinate system than latitude and longitude at the polar extremes. Students can further investigate coordinate systems such as google maps in the associated activity What's Wrong with the Coordinates at the North Pole?

Another common system of coordinates is UTM. It is different than latitude and longitude because when you actually look at it on the surface of the Earth, all of the lines, north-south lines (called easting) and east-west lines (called northing), meet at right angles. If you look at a globe, you can see that latitude-longitude does not do this. UTM is a projected coordinate system that is based on the Mercator projection, the same one that makes Greenland 14 times too large. So the world is already flat in this system, and it is easy to make the lines at right angles similar to Battleship. Another difference with UTM is that to know what a coordinate means, the zone of UTM must be specified. The same coordinate exists in every zone in the UTM system (60 zones), and so the coordinate is meaningless without the zone. Can you see the advantage to having a coordinate system that has every coordinate line at right angles? How might it be easier to measure distances or use a map for navigation with a "right-angle based" map?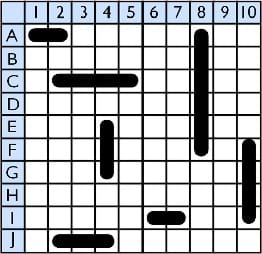

Lesson Background and Concepts for Teachers

A correct understanding of the meaning and use of coordinates and projections is absolutely essential to the use of paper maps and GIS. Most people do not think about coordinates beyond a simple understanding that latitude and longitude exist. A GPS on a hiking trail, a cell phone or as part of an onboard car navigation system show a blinking dot, and it is usually assumed to be correct. These measurements are generally accurate as presented on-screen (± a few meters), and part of the reason that it happens easily is because they all use the same coordinate system, which is World Geodetic System 1984 (WGS84). If coordinates are ever collected from a consumer grade GPS system, the coordinates may be collected in many different coordinate systems, but a calculation is done in the unit to deliver that coordinate. If that coordinate is then taken a step further and placed in a GIS with still a different coordinate system, then another transformation has occurred. If then still, that GIS uses a projection to display the spatial data then another transformation has occurred because the WGS84 from GPS is generally a geographic, un-projected coordinate reading. If anyone wants to use field-collected, downloaded, or hand-drawn GIS spatial data (for example, tracing an aerial photo), the importance of projection and coordinate becomes apparent. Students can explore GIS navigation with the fun associated activity Searching for Bigfoot and Others Like Him where students create their own GIS data layer in Google Earth

The study of the shape of the Earth, its measurement, and its representation is called geodesy. Concepts of the Earth as an ellipsoid, a sphere and a geoid all come from researchers in this field. Many texts can be consulted for greater information on these shapes, which in the end amount to some kind of model of the shape of the Earth that may be used on a map or in a GIS. For this lesson, it is less important to understand exactly how these models are generated and more important to know their level of accuracy in relation to the real Earth. One might think that the ellipsoid, since it is generally considered to be a less accurate representation of the Earth, would hardly be used today as compared with the geoid. This is, however, untrue. The Clarke 1866 ellipsoid, for example, was developed by Alexander Ross Clarke in that year, but it is still used today in the English-speaking world in the North American Datum 1927 (NAD27) coordinate system.

Many, many projections of the Earth's surface have been generated and are still being generated as part of research efforts today. Projections matter less and less the smaller the space that is being spatially represented, and yet those who need representation of large areas continually search for more efficient projections. Most of the classic projections of the globe change size, shape or angles of the continents and oceans. Some distort according to one category (for example, size) while others attempt to strike a balance between the two. The Mercator projection is a conformal projection because it preserves angles perfectly. This creates straight lines of latitude and longitude that make aerial and nautical navigation simpler because a single heading appears as a straight line. The Robinson projection stands in contrast to Mercator because it is a compromise of angles and size. It does not preserve either, but rather strives to present a nice overall view of the entire world. More recent efforts at creating projections abandon the need to have all spaces filled on the map. When the skin of an orange is broken as an analogy to demonstrate the breaking of the Earth in projections, the cartographer can choose a few ways to deal with the breakage—changes angles of objects or add extra land or water in the gaps. While some classic projections leave gaps at the break points, more recent projections leave the Earth as a broken object. These projections prefer to represent the individual continents and oceans more accurately rather than trying to preserve an overall unity in space.

Associated Activities

• Who Can Make the Best Coordinate System? - Students learn about coordinate systems in general by considering what they are expected do and who decided how they look. Then they make their own coordinate systems using a common area across all groups and compete to see who can make the best one. They analyze some work better than others and apply those observations to evaluating and choosing geographic coordinate systems commonly available today.

  Watch this activity on YouTube

• What's Wrong with the Coordinates at the North Pole? - Students complete a self-guided exercise in worksheet format combined with Google Earth that helps them explore practical and observable differences between different projection and coordinate systems. The activity improves their skills in using various Google Earth features.
• Searching for Bigfoot and Others Like Him - Cryptids, creatures of questionable existence, are used as a source of data to guide students into the creation of their own GIS data layer in Google Earth. The activity serves the purpose of a tutorial to teach students how to make data layers with a simple subject. Then they use that skill on other topics such as plastics in their neighborhood.

Lesson Closure

In a GIS, the projection and the coordinate system must be specified in order for anything to be displayed and for any analysis to be done. When using the system, if you do not understand the limitations of the projection or coordinate system, then any analysis you do might not be telling you what you think that it is telling you. Also, a great deal of calculation is required to convert between projections and coordinate systems in a GIS. Most GIS programs have that calculation already built in. You will get to experience the differences between coordinate systems in an activity involving Google Earth.

Vocabulary/Definitions

Albers conic equal area projection: A conic, equal area map projection that is centered over the north pole.

conformal projection: A map projection that guarantees that angles will be preserved, but shapes and size may not be.

easting: Refers to UTM and other similar coordinate systems (e.g., State Plane). The measurements in the system that are east and west.

ellipsoid: A three-dimensional geometric object that is generated by rotating an ellipse about an axis equivalent to its minor axis. It may also be thought of as simply a higher dimension analogue of an ellipse.

geodesy: The study of the shape of the Earth, its measurement, and its representation.

geoid: The equipotential surface of the Earth's gravity field that best fits, in a least squares sense, global mean sea level. [1]

GIS: Acronym for geographic information system. "A geographic information system (GIS) integrates hardware, software, and data for capturing, managing, analyzing, and displaying all forms of geographically referenced information." Source: www.esri.com; refer to the "What is GIS?" article for more details.

latitude: The angular distance measured north or south from the Earths' equator. It is not to exceed 90˚. If a north or south indication is not given for latitude then usually a negative sign (-) is used to differentiate south latitude from north latitude. [3]

longitude: the angular distance of a place east or west of the meridian at Greenwich or west of the standard meridian.

magnetic north: The direction that a standard compass points to as north. It is not necessarily the same as true north, and many maps gives an adjustment for the error, called the magnetic declination, to improve accuracy.

map projection: The result of projecting a sphere or spheroid (e.g., ellipsoid) onto a flat plane. Projections are sometimes created by mapping the spheroid or a piece of the spheroid onto a standard 3D object such as a cylinder or cone and then unrolling the 3D object so that it is flat.

northing: Refers to UTM and other similar coordinate systems (e.g., State Plane). The measurements in the system that are north and south.

prime meridian: The 0˚ line of longitude that passes through the Royal Observatory, Greenwich in London, UK. On the other side of the Earth, it meets with the International Date Line (180˚) to create a full circle.

Robinson projection: A standard map projection that is neither equal-area or conformal but rather attempts to strike a balance between either extreme in order to provide a more unified and accurate representation of the world. Unlike the Mercator projection, the longitude lines are now curved, but the size distortion of polar objects is reduced.

spatial information: Any set of information in prose, tabulated, in a database, or any other kind of medium that has some location associated with the information. Locations may be as general as a hand-drawn circle on an aerial photo or as complex as an xyz coordinate with respect to a particular coordinate system. Non-spatial data either has no location given with it, or it is a type of information in which it is not possible to give an accompanying location.

true north: The direction on the Earth that points to the North Pole.

universal polar stereographic (UPS) coordinate system: A coordinate system meant to be used in cooperation with UTM. It employs the use of a Cartesian coordinate system that centers on North and South Poles, and its usability only covers a specified area around the poles.

universal trans Mercator (UTM): A coordinate system based on an adjusted form of the Mercator projection (called the transverse Mercator projection) in which the cylinder used to make the projection is rotated 90˚. Coordinates in this system are Cartesian and are in reference to one of 60 global zones.

world geodetic system 1984 (WGS84): A standard coordinate system that uses the 1996 Earth Gravitational Model geoid and is referenced to the center of the Earth. Coordinates are given as latitude and longitude though the "prime meridian" used is slightly different from the classic Prime Meridian through Greenwich.

Assessment

Classwork/ Homework

Activity 2: What's Wrong with the Coordinates at the North Pole? As students complete the work in class, it should become clear what their grasp is on the material through observation and individual assistance. Answer key and student versions are both included. Be sure to adjust the worksheet locations if you want to make the questions involve locations that are more significant to your students. Also be certain to obtain the EarthPoint grids before attempting the activity. (Lesson2Supp_Proj and Coor Worksheet.docx and Lesson2Supp_Proj and Coord Worksheet_Answer Key.docx)

Additional Multimedia Support

• Google Earth installation (free to install).
• "Unfolding the Earth" short video from New Scienties, https://www.newscientist.com/video/?bclid=1904732932&bcpid=25196461001&bctid=55885952001
• The "What's Wrong with the Coordinates at the North Pole?" exercise requires some downloadable files from http://www.earthpoint.us/Grids.aspx (EarthPoint). It is easily obtained by sending an email to site owner Bill Clark (see contact info at http://www.earthpoint.us/Contact.aspx)

References

Copyright

Contributors

Supporting Program

Acknowledgements

This digital library content was developed by the University of Houston's College of Engineering under National Science Foundation GK-12 grant number DGE-0840889. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.