Quick Look
Grade Level: 8 (7-9)
Time Required: 30 minutes
Expendable Cost/Group: US $1.00
Group Size: 2
Activity Dependency:
Subject Areas: Data Analysis and Probability
Summary
Students learn about coordinate systems in general by considering questions concerning what it is that the systems are expected do, and who decided how they look. They attempt to make their own coordinate systems using a common area across all groups and compete to see who can make the best one. Then they analyze why it is that some systems work better than others and consider what those observations mean for evaluating and choosing geographic coordinate systems commonly available today.
Engineering Connection
Geographic coordinate systems are rarely designed by engineers today except for specific situations, such as chemical plants, where it makes sense to introduce an entirely new system rather than use a standard such as universal trans mercator (UTM). It is valuable to understand how coordinate systems were designed and implemented because engineers must choose what coordinate systems work best whenever they are doing any kind of GPS application.
This activity relates to engineering because it asks students to challenge conventional coordinates by letting them know that they can design a coordinate system just as well as anyone else. Often, having the motivation to design a new system, product or structure is an important skill for engineers. This activity also teaches that the design process naturally includes collaboration and critique, thus students should be prepared to explain and defend their decisions, exercises that contribute to finding the best design solutions possible for given situtations.
Learning Objectives
After this activity, students should be able to:
- Identify the value of coordinate systems in general.
- Explain that coordinate systems are arbitrary and may be changed according to need.
- Evaluate a coordinate system according to why it is or is not useful.
- Design and explain a coordinate system based on the given parameters; explain how this is part of the engineering design process.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Understand that a function is a rule that assigns to each input exactly one output. The graph of a function is the set of ordered pairs consisting of an input and the corresponding output.
(Grade
8)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Use devices to control technological systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Texas - Science
-
design and implement experimental investigations by making observations, asking well-defined questions, formulating testable hypotheses, and using appropriate equipment and technology;
(Grades
6 -
8)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- map of the area that the class will be using
- some Sharpie® markers, or slightly fatter tipped pens
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/uoh_dig_mapping_activity1] to print or download.Introduction/Motivation
Coordinate systems are important in concept and practice for geographical information systems (GIS). They serve two main functions. The most important function is to provide a system to uniquely locate any point on the map. That map might describe the surface of the Earth, the lunar surface [3], or the celestial coordinate system [4]. The other important function that coordinate systems provide is that of regionalization. If coordinates have zones (for example, UTM) or regions (for example, hemispheres in latitude-longitude), then places within those zones can be grouped together for different geographic regions.
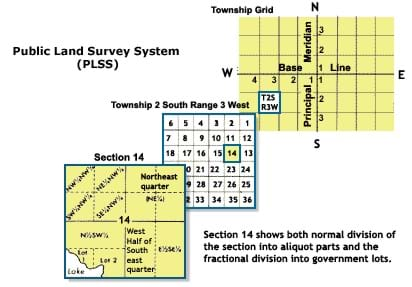
Geographic coordinates generally fall into two major types of grid systems. Some grid according to the accurate representation of the Earth as a curved surface. These coordinates are like latitude and longitude, they assume that the Earth is a spheroid of some kind, and thus when they are projected onto a flat map, they show curvature and non-orthogonality. Other coordinate systems such as UTM take the Earth as a projection and then place perfectly orthogonal straight lines on top of that projection. For accuracy, the methods that allow curves are better, but from a usability standpoint, the orthogonal systems are better. A prime example of a historic use of regular orthogonal coordinates is that of township, range and section as used in the the Public Land Survey System. This system was developed to efficiently divide the American West into land cadastres that could easily be organized and sold to settlers who did not already know landmarks in the area by which to measure property boundaries. [5]
One coordinate system is not necessarily better than another because many things about coordinate systems are arbitrary. A common example is the initial location of longitude lines in a standard geographic coordinate system. Zero degrees longitude runs through Royal Observatory, Greenwich, UK, but it could have just as easily have been any other place. Even the numbering systems used in many coordinate systems are arbitrary. Milton Bradley's game Battleship uses Latin letters to describe rows and columns. They could just have easily used Greek letters with numbers.
The point of this exercise is for each student to take the same geographic area given in the form of some kind of map and to design a better coordinate system that they think makes sense to them. Each student (or group) that participates will have a few minutes to draw the coordinate system directly onto the map in any fashion that they choose. No convention at all is required. Encourage students to apply their creativity and understanding of maps to solve this engineering challenge. The only requirement is that each location has a coordinate (or coordinates) that describes it uniquely from all other locations. When the time is up, we'll ask each student to explain their coordinate system and then ask the class what they like and dislike about each system. You should discover that there are many different systems that could be used and what you choose to use will be according to how you want to describe the map and the locations on it that are more important to you. Explain to students that engineers can define new measurement systems to help them better gather and analyze data.
Procedure
Before the Activity
- Print out maps in a large enough size and resolution to see details. Print enough to accommodate the number of groups expected per class.
- Group size note: Groups may be composed of 1-4 students.The goal is to have students think creatively about coordinate systems. If a group of four can have everyone participate, then the group can be that large. If this is not the case, then organize smaller group sizes (all the way down to one) so that all members of each group have input into the coordinate system they design.
- (optional) Set up a "coordinate designing song" (such as something techno) to play in the background during the timed period of the design. It can highten the competitive feel between the groups.
With the Students
- Discuss coordinates with students. What do coordinates do? Why are they necessary in maps and GIS? What requirements do they have, and why are they the way they are? Are latitude and longitude something obvious when you look at a globe? Would everyone have made that choice of coordinates, or did someone have to choose it for some designed purpose?
- Discuss some examples of common coordinate systems that might be encountered. Geographic coordinates, projected coordinates (UTM, State Plane), planetary coordinates (such as Mars), celestial coordinates, Battleship, and possibly even something as applied as grids used for archaeological digs. Highlight the utility of the system. It wasn't necessarily chosen because it looked pretty but because it accomplished something specific for navigation, classification or property identification.
- Introduce the map that you are going to use for the class and explain to them that it has no coordinate system. Then give the maps to the groups and tell them they will have 2-3 minutes to design the best coordinate system that they can right there on the map.
- Begin the timer, and let the designing happen.
- Conclude by asking students to explain the coordinate system choices (or at times showing that they did indeed make choices) and asking other students to judge the usefulness of the various systems. Also explain how engineers often build off of systems that are currently used to make them "better" for helping solve a specific problem. In this case, the given problem is mapping a certain area.
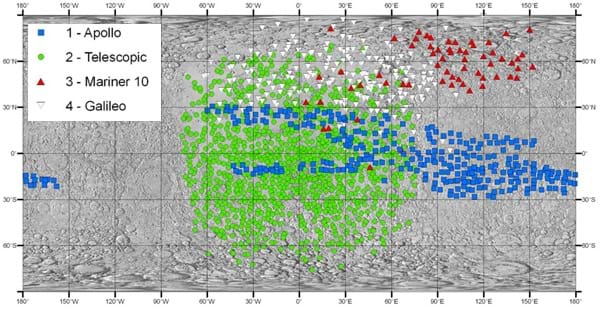
Figure 3. An example of the selenographic coordinate system that is used on the Earth's moon. This example shows the locations of particular NASA satellites and landings on and around the lunar surface.
Vocabulary/Definitions
cadastre: An official register of the quantity, value, and ownership of real estate used in apportioning taxes. [6]
orthogonality: The property of coordinates that indicates whether the grid lines are or are not at right angles to each other.
Assessment
Pre-Activity Assessment
Coordinate System Familiarity: See how many different types of coordinate systems or coordinate system related concepts students already know and write them on the board. Make a count of how many different systems can be identified and how many different types of spatial areas are described by these systems (for example, particular cities, other planets, the ocean, the brain, etc.). Expect that most students do not know more than geographic latitude and longitude, but this is an opportunity to inform them of the reality that our geographic coordinate systems exist as they do simply because people decided to make them that way. Really, any coordinate system could have been devised that made sense for their purposes.
Activity Embedded Assessment
Student Engagement: As participating students are drawing their coordinate systems, assess whether the spectator students are thinking about the concepts. Ask questions like, "Why do you think they are doing the coordinate system that way?" "Do you think what they are doing will work?" or "How would you have done a coordinate system?"
Post-Activity Assessment
Examine the Results: Have students who drew the coordinates explain why they chose the coordinates that they did. As the facilitator, notice if some students chose to center their system on the center of the map (for example. a downtown area) or to make their coordinates non-orthogonal. Some students may have inadvertently created a coordinate system that is interesting, but it might be difficult to understand or may generate locations that are described by more than one coordinate pairing. Ask questions that challenge students to realize the consequences of their choices for their system. For the spectator students, ask them questions that elicit comparison between the coordinate systems. Which would you use? Why would you choose that one? How could this system be improved? What is unusual or novel about this system that you never thought about before? How would you begin to show distances in this coordinate system?
Troubleshooting Tips
Students may have trouble beginning to think about what kind of coordinate system they want to design for the map. Give them examples of simple coordinate systems such as those used in the Battleship game or an amusement park map to help get them thinking.
Activity Scaling
- For lower grades, use larger groups so that students can combine ideas. Also, you may want to add some elements to the coordinate system and let them finish it out. For example, put some sort of grid lines in place and let students decide on the labeling scheme or if they want to further subdivide the grid.
- For upper grades, have students work more independently and possibly give them additional requirements such as use of color-coding or a need to define the system according to particular units of measure. For example, require students to choose a standard grid size according to the use of the map and explain why that grid size is appropriate.
Additional Multimedia Support
Online Game: Generate additional excitement about coordinates through an online version of Battleship, http://www.learn4good.com/games/board/battleship.htm
Video: Discovering Math: The Rectangular Coordinate System. The introduction is useful to explain how latitude-longitude was developed and how it is used. http://videos.howstuffworks.com/hsw/25069-discovering-math-the-rectangular-coordinate-system-video.htm
Map Documents: For the coordinate drawing, use either of the maps provided in the Maps Useful for Coordinate System Drawing. (These maps of Nashville and Waco are also listed in the References section). The only requirement is that the map be fairly simple and not already have some obvious coordinate system on it.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students complete a self-guided exercise in worksheet format combined with Google Earth that helps them explore practical and observable differences between different projection and coordinate systems. The activity improves their skills in using various Google Earth features.

Students learn about projections and coordinates in the geographic sciences that help us to better understand the nature of the Earth and how to describe location.

Students explore using a GPS device and basic GIS skills. They gain an understanding of the concepts of latitude and longitude, the geocaching phenomenon, and how location and direction features work while sending and receiving data to a GIS such as Google Earth.

Through an adult-led field trip, students organized into investigation teams catalogue the incidence of plastic debris in different environments. They investigate these plastics according to their type, age, location and other characteristics that might indicate what potential they have for becoming...
References
Map of Atlanta, GA, 1919. In The Automobile Blue Book Publishing Co., 6th edition. University of Texas Libraries. http://www.lib.utexas.edu/maps/historical/atlanta_ga_1919.jpg
Map of Milano, Italy, 1913. Baedeker, K. In Baedeker's Northern Italy Handbook For Travelers, 14th edition. University of Texas Libraries. http://www.lib.utexas.edu/maps/historical/milano_1913.jpg
About Map Projections. ESRI, ArcGIS 9.2 Help Accessed March 25, 2010. http://www.esri.com/about-esri/about/history.html
Map Projections with Tissot's Indicatrix. Wikimedia Commons. Accessed March 25, 2010. http://commons.wikimedia.org/wiki/Category:Map_projections_with_Tissot's_indicatrix
A Standardized Lunar Coordinate System for the Lunar Reconnaissance Orbiter; LRO Project White Paper Version 4. May 14, 2008. NASA Goddard Space Flight Center: Greenbelt, MD, 2008. http://pds-imaging.jpl.nasa.gov/documentation/LRO_Coordinate_System.pdf
Astronomical Coordinate Systems, Students for the Exploration and Development of Space (SEDS). Accessed March 24, 2010. http://spider.seds.org/spider/ScholarX/coords.html
The Public Land Survey System (PLSS). National Atlas. Accessed March 24, 2010. http://www.nationalatlas.gov/articles/boundaries/a_plss.html
Merriam-Webster Online. Accessed March 18, 2010. http://www.merriam-webster.com
Map of Nashville, TN, 1919. In The Automobile Blue Book Publishing Co., 1919. University of Texas Libraries. http://www.lib.utexas.edu/maps/historical/nashville_tn_1919.jpg
Map of Waco, TX, 1892. In U.S. Geological Survey, 1892. University of Texas Libraries. http://www.lib.utexas.edu/maps/historical/waco1898.jpg
Copyright
© 2013 by Regents of the University of Colorado; original © 2010 University of HoustonContributors
Nathan Howell; Andrey KoptelovSupporting Program
National Science Foundation GK-12 and Research Experience for Teachers (RET) Programs, University of HoustonAcknowledgements
This digital library content was developed by the University of Houston's College of Engineering under National Science Foundation GK-12 grant number DGE 0840889. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.
Last modified: May 5, 2021









User Comments & Tips