Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00 (activity can also be done individually so students can keep their quadrants)
Group Size: 2
Activity Dependency: None
Subject Areas: Earth and Space, Geometry, Measurement
Summary
Celestial navigation is the art and science of finding one's geographic position by means of astronomical observations, particularly by measuring altitudes of celestial objects — sun, moon, planets or stars. This activity starts with a basic, but very important and useful, celestial measurement: measuring the altitude of Polaris (the North Star) or measuring the latitude.
Engineering Connection
Mathematical words and concepts used in celestial navigation, such as angle, average, quadrant and elevation, are common vocabulary for all types of engineers. For example, an environmental engineer might wish to collect water samples from a polluted stream, compute the average toxin level, and see if the stream elevation has any effect on the toxicity. Measuring altitudes and angles are also important in the work of aerospace engineers who position satellites in orbit, and civil engineers who design structures.
Learning Objectives
After this activity, students should be able to:
- Explain the advancement of navigational techniques based on historical contributions.
- Invent a simple device to read latitude.
- Describe the interactions of objects in the universe.
- Explain how the measurement of angles and altitudes is used in engineering.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
-
Patterns of the apparent motion of the sun, the moon, and stars in the sky can be observed, described, predicted, and explained with models.
(Grades 6 - 8)
More Details
Do you agree with this alignment?
-
Technologies extend the measurement, exploration, modeling, and computational capacity of scientific investigations.
(Grades 6 - 8)
More Details
Do you agree with this alignment?
Common Core State Standards - Math
-
Describing the nature of the attribute under investigation, including how it was measured and its units of measurement.
(Grade
6)
More Details
Do you agree with this alignment?
-
Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including the perpendicular bisector of a line segment; and constructing a line parallel to a given line through a point not on the line.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on a single count or measurement variable
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Describe the nature of the attribute under investigation, including how it was measured and its units of measurement.
(Grade
6)
More Details
Do you agree with this alignment?
-
Summarize, represent, and interpret data on a single count or measurement variable.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Make formal geometric constructions with a variety of tools and methods.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Describe methods and equipment used to explore the solar system and beyond
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- 1 straw or 12-inch ruler (straws if students will keep the quadrants)
- 1 piece of string (about 6 inches)
- 1 sheet of poster-board or stiff paper (such as two pieces of construction paper glued together)
- 1 small weight (such as a washer, metal nut or any small, heavy object)
- 1 protractor (if available; share with other groups if necessary)
- tape
- 1 pencil
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_navigation_lesson02_activity2] to print or download.Introduction/Motivation
How did ancient navigators planning to sail out of sight of land stay on course and return home? (Answer: They measured the altitude of Polaris, the North Star, when they left homeport.) In today's terms, this would be called measuring the latitude of the homeport.
How did knowing the latitude of Polaris enable them to find their ways home? (Answer: To return after a long voyage, early navigators needed only to sail north or south, as appropriate, to bring Polaris to the altitude of homeport. Then they would turn left or right, as appropriate, and "sail down the latitude," keeping Polaris at a constant angle.)
In this activity, you will learn the basics of celestial navigation.
Procedure
Background
Because the Earth rotates 360 degrees in one day, the stars appear to move across the sky just like the sun. Actually, the stars are stationary (relative to us), and we rotate around them — just like we rotate around the sun. Polaris is the only bright star in the Northern hemisphere that does not move (not much, anyway), while all other stars do move, as seen in the Star Trails Worksheet. This lack of movement by Polaris is because it is almost directly above the spin axis of the Earth.

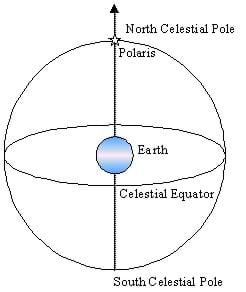
Before the Activity
- Decide whether to have students make paper or protractor quadrants (see below). If paper is chosen, make enough copies of the Make a Paper Quadrant–Instructions Sheet.
- If you want students to be able to take home/keep their quadrants, then have them work individually, rather than work in pairs.
- Print out the Polaris Latitude Worksheet, as needed.
- Print one or more copies of the Star Trails Sheet.
- Cut out a paper star or picture of a star and place it high in the center of a classroom wall (the higher the better!) to serve as the classroom's North Star.
With the Students
- Show the students the Star Trails Sheet, either as an overhead or hold it up. Ask what the picture is of, and have students brainstorm ideas of why it looks the way it does. Try to elicit more in-depth explanations of the pattern and the star in the middle, explaining that the picture is of star trails due to the Earth's rotation. Guide students to the idea that Polaris, the North Star, does not move because it is directly above the Earth's axis of rotation. Why is Polaris not directly overhead when we look at the night sky? (Answer: Because we are not at the North Pole.) How high is Polaris in the sky? (Answer: It depends on where you are.) The North Star can help you find out where you are on Earth.
- Give students a Polaris Latitude Worksheet, and ask them to follow the instructions. Have them use the principle described on the worksheet to determine the latitude of their desks in the classroom. Point out the classroom's "North Star" and ask students: "Does anyone have a protractor big enough to measure the angle to the star? No? Well, it is time to do some engineering!"
- Give each student a "Make a Paper Quadrant–Instructions" Sheet, and follow the instructions. If not enough protractors are available, make Protractor Quadrants (see instructions below). (Note: Have them use paper if you want them to be able to keep their quadrants.)

a. Tape a straw or ruler to the protractor so that it lies along both the 90-degree and center mark of the protractor (that is, so it bisects the half-circle protractor).
b. Tie or tape a 6-inch piece of string to the center hole of the protractor, making sure the string hangs freely.
c. Tie a weight to the other end of the string. The string should lie along the 0-degree mark of the protractor if the straw or ruler is held parallel to the ground.
- Direct students to determine the relative latitude of their desks by positioning their eyes, along with their quadrants, level with the edge of their desks.

- Find the classroom's North Star elevation by sighting through the straw, or by touching a ruler to your cheekbone (under your eye) and then pointing the other end directly at the star.
- Let the weight swing freely until it stops so that the string is hanging straight down.
- Have your partner read the scale. If working alone, slightly tilt the stick so that the string touches the quadrant scale. Then with your finger and thumb, hold the string against the scale, and bring the scale end around where you can read it. Record this measurement on the back of your worksheet.
- Trade positions with your partner and have him/her take a second measurement. Record this measurement on the back of your worksheet.
Assessment
Pre-Activity Assessment
Brainstorming: In small groups, have students engage in open discussion. Remind students that no idea or suggestion is "silly." All ideas should be respectfully heard. Show them a picture of star trails, like the one in the Lesson Background section and ask them the following question. Then have them share their ideas with the class before explaining star trails to them.
- What are we seeing in the night sky in this photograph? Why does it look like that? (Answer: It is a photograph of "star trails" created by the Earth's rotation. It is formed by taking many consecutive exposures of the night sky so that we can see the relative movement between us on Earth and the stars in the universe.)
Activity Embedded Assessment
Worksheet: Have students fill out the worksheets during the activity. Review their answers to assess their comprehension of the subject. Using the Polaris Latitude Worksheet, students measure angles on paper and then calculate the latitude of their desks relative to the classroom's simulated North Star.
Post-Activity Assessment
Problem Solving: Have students engage in open discussion to come up with solutions to questions/problems. For example, now that they have become celestial navigators, ask them to guess the latitude of the photo location of the Star Trails Sheet. (Answer: About 5-10 degrees north of the equator.)
Safety Issues
Alert students to use caution if using rulers near their eyes to sight the classroom's North Star.
Troubleshooting Tips
Although it may be tricky to get the paper and/or protractor quadrant reading precise the first time, encourage students to keep trying. Make sure they let the weighted string come to a complete rest before taking the quadrant measurement.
Activity Extensions
Have students use the quadrants that they made in this activity to measure the elevation of the real North Star. Then, compare the answers to your city's latitude. Assign this as homework or in class if extra time is available.
Using the Polaris Latitude Worksheet, have students pick another latitude line on the Earth picture and draw their own tangent lines to that point. Then, have them measure the angle between the new tangent line and the line to Polaris to see if it matches their latitudes. Will this technique work at all locations on the Earth? (Answer: No. It will not work anywhere in the Southern Hemisphere because the North Star is not visible there. However, other celestial measurements can be made anywhere on Earth to measure latitude.)
Activity Scaling
- For 6th grade, do activity as is.
- For 7th grade, plot and discuss differences in results of the desk latitudes found. If a row of desks is facing the wall with the star, do students at the ends of the row have different latitudes values than those in the middle? (Answer: Yes, they could because the ends of the row are farther from the star and therefore see a slightly smaller angle.) Is the difference in latitude of the nearest two rows to the star the same as the difference between the farthest two rows? (Answer: The first two rows should have a larger difference because the room is flat. The further you are from the star, the less effect moving back one row has on the angle of the star.)
- For 8th grade, choose a city along a line of latitude about 140 miles directly south of the city you are in. Tell students that the height of Polaris when viewed from that city is about 2 degrees LOWER than the height you see in your city. From this information, challenge them to come up with an estimate of the Earth's circumference. (Answer: Divide 140 miles by 2 degrees, and you find that 1 degree of latitude is equal to 70 miles. The Earth, a circle, has 360 degrees. Multiply that by 70, and you come up with 25,200 miles — very close to the circumference of the Earth at the equator, which is about 24,900 miles or 40,070 km.)
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

In this lesson, students learn how great navigators of the past stayed on course — that is, the historical methods of navigation. The concepts of dead reckoning and celestial navigation are discussed.
References
"Dometrails." September 2, 2000. Online image. Astronomy Picture of the Day. Accessed October 26, 2003. http://antwrp.gsfc.nasa.gov/apod/image/0009/dometrails_cfht_big.jpg>.
Woodfill, Jerry. Medieval and Twentieth Century Navigation. August 28, 2002. National Aeronautics and Space Administration. Accessed October 16, 2003. http://vesuvius.jsc.nasa.gov/er/seh/navigate.htm>
Copyright
© 2004 by Regents of the University of ColoradoContributors
Matt Lippis; Penny Axelrad; Janet Yowell ; Malinda Schaefer ZarskeSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under grants from the Satellite Division of the Institute of Navigation (www.ion.org) and the National Science Foundation (GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: December 19, 2024






User Comments & Tips