Lesson Not So Lost in Space

Learning Objectives

After this lesson, students should be able to:

• Understand the basic concept of an orbit around the Earth or sun.
• Understand the types of measurements that are made from Earth to track interplanetary spacecraft.
• Understand satellites and their usefulness in space exploration.
• Understand that navigational technology is based on fundamental math and science concepts

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

NGSS: Next Generation Science Standards - Science

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Introduction/Motivation

Ask students if anyone knows the name of the first artificial satellite launched into orbit around the Earth. (Answer: On October 4, 1957, the Soviet Union launched Sputnik I.) How many satellites would you guess are currently orbiting the Earth? (Answer: about 3,000)

Ask students if they know the names of current space exploration missions that go beyond the Earth. (Answer: The Galileo spacecraft recently ended a 14-year mission to the planet Jupiter and its moons by crashing into the planet on Sept 21, 2003. The 2003 Mars Exploration Rovers are currently enroute to Mars, expecting to arrive in January 2004. More recently, the Mars Curiosity Rover was launched in 2011 and is currently sending us information and pictures about Mars. You can find detailed information on NASA (National Aeronautics and Space Administration) missions at: https://www.jpl.nasa.gov/missions/)

How do these spacecraft get from Earth to other planets? Is it like driving a car or flying an airplane? How do they know where they are along the way and when to make adjustments? In this lesson, we explore how space agencies like NASA keep track of where these interplanetary travelers are and how to get them to their destinations.

Lesson Background and Concepts for Teachers

Planetary Orbits

The motion of planets or spacecraft around the sun is governed primarily by the gravitational attraction between the central body (the sun or planet) and the secondary body (the planet or spacecraft). The same is true for a satellite traveling around the Earth or other planet, where the Earth is now the central body and the satellite is the secondary body. Hold on...if gravity attracts the planets towards the sun and satellites towards the Earth, what keeps all this stuff from colliding? [Possible answers students may give: There is no gravity up in space (not true). There is only a little gravity (this is true – Newton found that if the distance from the center of Earth doubles, gravity is a quarter as large as what it is at the surface of Earth. But, with some gravitational force, this question still applies). Actual answer: The Earth is moving tangentially to the sun at a speed high enough to counteract the attracting force of sun's gravity. Similarly, if a satellite is given speed in any direction tangent to the surface of the Earth, it will curve and follow a trajectory around the Earth]. Without the gravity of the Sun, the Earth would travel away from the Sun. However, without the speed of the Earth, the Earth would fall into the Sun. Those two counteracting forces create the orbit. The same applies to satellites orbiting around Earth. In fact, at a distance of 100 km, a satellite needs to be moving at 8 kilometers per second to stay in orbit. At a higher altitude, satellites can travel slower.

The trajectory, or path, of a planet or spacecraft is referred to as an orbit. In the early 1600s, Johannes Kepler described the orbits of planets in his famous "Three Laws":

1. The orbit of each planet is an ellipse with the sun at the focus.
2. The line joining the planet to the sun sweeps our equal areas in equal times.
3. The square of the period of a planet is proportional to the cube of its mean distance to the sun.

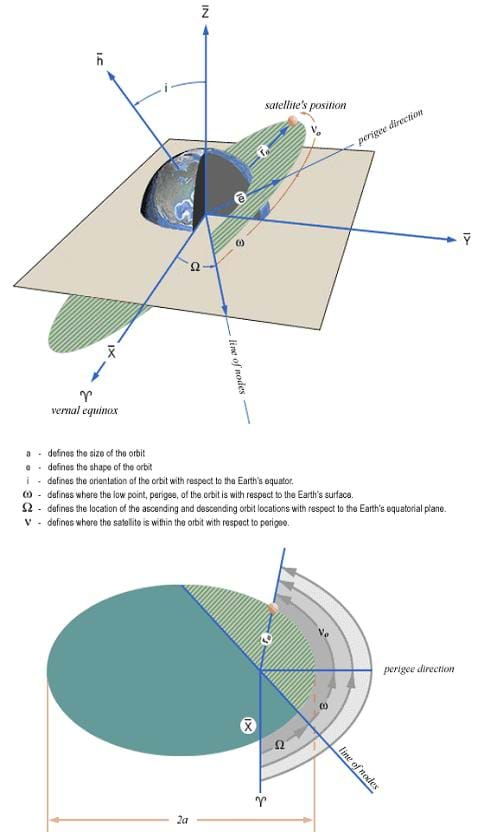
Kepler's laws were based on empirical evidence: observations of the planet Mars made by Tycho Brahe. At the time, Keple hoped that he would be able to describe planetary motion by circles, but the experimental evidence proved otherwise, and he was forced to resort to a little-known geometrical shape — the ellipse. It is interesting to note that Kepler did not understand the physics of why planets followed these paths; but rather just described mathematically what he found in the data. Roughly half a century later, Sir Isaac Newton filled in the gap, explaining the physics of the motion with his famous laws of motion and gravitation. Orbits of planets about the sun and satellites about the Earth are typically described by six Keplerian elements (Figure 1).

They can be divided into parameters that describe the size and shape of the orbit:

a - The semimajor axis (a) is the longest axis of the ellipse going through the two foci.

e - The eccentricity (e) describes the elongation of the ellipse. The distance between the two foci can be computed as 2ae.

And the orientation of the orbit plane:

Ω – The right ascension of the ascending node (Ω) describes where the orbit crosses the equatorial plane relative to a reference direction known as the vernal equinox.

i – The inclination of the orbit (i) describes how the orbit plane is tipped relative to the equatorial plane.

ω – The argument of perigee (ω) describes where the point of closest approach to the planet lies within the orbit plane. It is an angle measured in the plane of the orbit from the ascending node to the point of closest approach.

θ – The last parameter describes where the planet or spacecraft is within its orbit, measured from the perigee and given the unusual name of "true anomaly" (θ).

When an orbit is not circular, it has only one point that is closest to the central body and one point that is farthest from the central body. The closest point is known as the periapse and the farthest point is known as the apoapse. If the central body is the Earth, these points are also referred to as the perigee and apogee, respectively. Similarly, if the central body is the sun, the names change to perihelion and aphelion.

Very clear and accessible information on orbits and definitions can be found at: https://solarsystem.nasa.gov/basics/

Planets in the solar system all travel in orbits with the sun at the focus. Most planets are in almost circular orbits with both foci at the sun. The orbits of Mercury and Pluto are both somewhat elliptical with eccentricities of 0.2 and 0.5, respectively. The eccentricity of Pluto's orbit causes it to sometimes travel inside the nearly circular adjacent orbit of Neptune.

According to Kepler's laws, if you know the semimajor axis of the orbit, you can find the orbit period (i.e., how long it takes to travel around the central body). The period of an orbit is given by:

P = 2 π SQRT( a³ / μ)

Where a is the semimajor axis of the orbit and μ is the gravitational constant for the central body. For Earth it is: μ_E=398600 km³/s². From this, you can see that the larger the orbit, the longer the period. For a circular orbit you can also compute the speed at which the object travels as follows:

s = SQRT( μ/ a )

This shows that the smaller the semimajor axis (i.e., the smaller the orbit), the faster the speed at which the satellite must travel. For example, the International Space Station in orbit around the Earth has a semimajor axis of about 6756 km. So, using the equation for the period given above, we find that its period is about 5,526 seconds or 92 .1 minutes. Using the speed equation, we can calculate its speed as 7.68 km/s. In comparison, a TV broadcasting satellite, in a geosynchronous orbit around the Earth, has an orbital period of 24 hours!

To get from one orbit to another, a spacecraft must transfer to an elliptical path that connects its current orbit to the desired orbit. A simple way to do this is the Hohmann transfer. To execute a Hohmann transfer, a spacecraft fires thrusters tangentially along the direction of travel for a short burst. This initial "delta-v" changes the energy of the orbit to put it on an elliptical path. The periapse of the new orbit is at the starting orbit, and the apoapse of the orbit is at the target orbit. After half an orbital period, the satellite is at the right altitude for its new orbit, but it must again increase its speed to stay in the new higher orbit. A second delta-v is performed to circularize the orbit at the higher altitude. The Hohmann transfer is efficient for fairly small orbital changes. More complex maneuvers using gravity-assist fly-bys are also used to provide more efficient transfers to distant planets.

Measurements

Unmanned satellites and spacecraft are generally tracked by ground stations to determine their orbits. NORAD (the North American Aerospace Defense Command) currently tracks all objects larger than 30 cm in orbit around the Earth. NASA's Deep Space Network (DSN) is used to track interplanetary craft. Commercial satellites are tracked by private ground stations, and some satellites (like the GPS satellites) have their own dedicated tracking networks. A tracking station receives transmissions from the satellite and may also send out a ranging signal that is reflected or echoed by the satellite.

Three basic types of ground-based measurements are used to determine an orbit: range, Doppler, and angles.

Angle measurements are the most straightforward and generally the least accurate type of measurement. A ground station antenna connected to a receiver is scanned to find the highest signal power from the satellite. The antenna sweeps horizontally across in azimuth and vertically in elevation. When it locks on to the signal, the azimuth and elevation angles of the antenna indicate the direction to the satellite. By making a sequence of angle measurements over time, the orbit of the satellite can be estimated.

Range measurements can be made by timing the arrival of marked pulses or symbols in the communications link. The ground station transmits a signal to the satellite or spacecraft and the spacecraft receives and retransmits this signal. This is known as a transponder. The ground station measures the roundtrip time of the signal, divides by 2, and multiplies by the speed of light to find the range to the satellite. More precise measurements can also be made by using more than one ground station on the Earth. Differences between ranges measured at the different stations allow delays in the transponder to be determined and permit much more precise ranging measurements.

Doppler measurements represent the rate of change of range to the satellite. They are a measure of frequency shift of a transmission. Assume that a transmitter at rest emits a signal or tone of a certain frequency that we will call the base frequency. When a transmitter approaches a receiver, the receiver hears or senses a higher frequency than the base frequency. At the "point of closest approach," that is, when the transmitter and receiver are as close as possible, the received frequency is equal to the base frequency. As the transmitter moves away from the receiver, the received frequency is lower than the base frequency. The figure below illustrates the Doppler shift as a function of time as a satellite in a low Earth orbit moves overhead a ground station. The closer to directly overhead the satellite moves, the more dramatic the Doppler shift will be. Scientists can use a sequence of Doppler measurements to determine the orbit of a satellite or spacecraft.

Today, orbit determination programs use all available measurement types to form the best estimate of a satellite's trajectory. The accuracy of the estimates depends on the type of orbit and the quality and quantity of observations from the ground.

Sightings

Many near-Earth satellites can be seen using a backyard telescope. A few are also visible to the naked eye. A good example is the International Space Station (ISS). The ISS is a very large structure, 3,300 sq. ft. in area, in an almost circular low-Earth orbit, about 250km above the surface of the Earth. The inclination of the orbit is 51.5 deg. Because of its large size and reflective surfaces, and under good viewing conditions (on a clear night when the sun's rays hit it just right), you can see the station pass across the sky with your naked eye (no telescope).

To observe a satellite (or planet or comet), you will need to know what time and where it will rise and set in the sky for your location on Earth. You will also need to know the quality of the "viewing conditions;" that is, how well it will be illuminated by the sun. 

Associated Activities

• A Roundabout Way to Mars - Students will use a cardboard and strings to explore Earth and Mars orbits around the sun and a transfer orbit from one to the other.

  Watch this activity on YouTube

Lesson Closure

Ask students about the difference between driving a car and guiding a satellite from one orbit to another. Does a planet like Venus that is in an orbit close to the sun, travel faster or slower than a planet like Jupiter that orbits farther from the Sun? (Answer: Closer-in planets travel faster. They need the extra velocity to counteract the higher gravitational attraction.) From your location, which way does the space station move across the sky? (Answer: From most areas of the continental US, the passes will be W to E, sometimes SW to NE or other variations. They last for a few minutes and sometimes reach fairly high elevations.) How would it look from the North Pole? (Answer: The satellite would only appear at very low elevations and skirt across near the horizon.)

Vocabulary/Definitions

azimuth: The angle measured at an observer's location in the horizontal plane between an object and the direction to North.

central body: A massive object (like the sun or a planet) that attracts a satellite or planet. Orbit – The closed path a satellite or planet takes around a central body.

doppler: The frequency shift of a signal due to motion of the transmitter and receiver.

elevation: The angle measured at an observer's location between the direction to an object and the horizon.

Keplerian elements: Six parameters that describe the size, shape, and orientation of an orbit.

range: The straight-line distance from an observer to the object observed.

trajectory: The path taken by a spacecraft.

Assessment

Pre-Lesson Assessment

Question/Answer: Ask the students and discuss as a class:

• Ask students if anyone knows the name of the first artificial satellite launched into orbit around the Earth. (Answer On October 4, 1957, the Soviet Union launched Sputnik I.)
• How many satellites would you guess are currently orbiting the Earth? (Answer: about 3,000)

Post-Introduction Assessment

Voting: Ask a true/false question and have students vote by holding thumbs up for true and thumbs down for false. Count the votes, and write the totals on the board. Give the right answer.

• True or False: Unmanned satellites and spacecraft are generally tracked by ground stations to determine their orbits. (Answer: True)

Post-Lesson Assessment

Practice Problem: Calculate the orbit period of the earth: a = 1.496 x 10⁸ km and μ = 1.327 x 10¹¹ km³/s².

(Answer: P= 2π*sqrt(a³/μ) = 2π*sqrt( (1.496 x 108 km)³/(1.327 x 10¹¹ km³/s²) ) =3.156 x 10⁷ seconds = 365.3 days!)

Bingo: Provide each student with a sheet of paper containing a list of the lesson vocabulary terms. Have each student walk around the room and find a student who can define one vocabulary term. Students must find a different student for each word. When a student has all terms completed s/he shouts "Bingo!" Continue until two or three students have bingo. Ask the students who shouted "Bingo!" to give definitions of the vocabulary terms.

Lesson Extension Activities

Have students interested in hands-on construction of a satellite, visit the following NASA website: https://www.jpl.nasa.gov/missions/. This website has a build-your-own DSN station activity as well as contains a lot of interesting video clips of the Mars missions and other missions

For more advanced students, have them look up the orbital period and radius of each of the planets. Graph the period as a function of the radius.

References

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.