Quick Look
Grade Level: 8 (6-8)
Time Required: 30 minutes
Expendable Cost/Group: US $5.00 Under $5 total (minimal or none, depending on office-type supplies that are available).
Group Size: 2
Activity Dependency: None
Subject Areas: Algebra, Earth and Space, Geometry, Measurement
NGSS Performance Expectations:

| MS-ESS1-2 |
Summary
Students explore orbit transfers and, specifically, Hohmann transfers. They investigate the orbits of Earth and Mars by using cardboard and string. Students learn about the planets' orbits around the sun, and about a transfer orbit from one planet to the other. After the activity, students will know exactly what is meant by a delta-v maneuver!
Engineering Connection
Aerospace engineers must be creative when planning the best routes and methods to send a spacecraft from Earth to another planet since space travel is never a direct linear path, but involves transfers between circular orbits. Engineers apply their understanding of math, especially geometry, to determine the most efficient interplanetary trajectories, and thus minimize costs by reducing the need for supplies and fuel as much as possible. They design techniques that take advantage of gravity and the behavior of forces in space.
Learning Objectives
After this activity, students should be able to:
- Describe the geometry of circles and ellipses.
- Use scaling factors.
- Describe space travel and Hohmann transfers.
- Explain the relationship between space travel technology and other fields of study (i.e. mathematics).
- Explain how orbits exist.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-ESS1-2. Develop and use a model to describe the role of gravity in the motions within galaxies and the solar system. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Develop and use a model to describe phenomena. Alignment agreement: | Earth and its solar system are part of the Milky Way galaxy, which is one of many galaxies in the universe. Alignment agreement: The solar system consists of the sun and a collection of objects, including planets, their moons, and asteroids that are held in orbit around the sun by its gravitational pull on them.Alignment agreement: The solar system appears to have formed from a disk of dust and gas, drawn together by gravity.Alignment agreement: | Models can be used to represent systems and their interactions. Alignment agreement: Science assumes that objects and events in natural systems occur in consistent patterns that are understandable through measurement and observation.Alignment agreement: |
Common Core State Standards - Math
-
Fluently divide multi-digit numbers using the standard algorithm.
(Grade
6)
More Details
Do you agree with this alignment?
-
Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Fluently divide multi-digit numbers using standard algorithms.
(Grade
6)
More Details
Do you agree with this alignment?
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.
(Grade
7)
More Details
Do you agree with this alignment?
Colorado - Science
-
Describe methods and equipment used to explore the solar system and beyond
(Grade
8)
More Details
Do you agree with this alignment?
-
Recognize that mathematical models are used to predict orbital paths and events
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each group should have:
- Cardboard (about the size of, or slightly larger than, 8½" x 11")
- A few sheets of white paper (8½" x 11")
- Thread
- 4 Pens or pencils in different colors
- 6 Pushpins
- Ruler
- Scissors
Introduction/Motivation
Space travel is one of the most exciting, high tech, and challenging fields in engineering. In 1961, Soviet cosmonaut Yuri Gagarin was the first human in space. In 1969, American astronaut Neil Armstrong was the first human to walk on the moon. Aerospace technology has developed enormously since then, and aerospace engineers continue to seek safe and efficient ways to travel in space.
When imagining space travel, one should think of it not as a direct linear path from point A to point B, but more like a transfer between circular orbits. It is possible to travel in a straight line from A to B; but in the vicinity of a planet or star, the gravity of the planet or star causes the natural motion of objects to follow an elliptical (or hyperbolic) path. All objects have a natural attraction between them, called gravity, which is relative to their masses and distance apart. A huge amount of fuel would be needed to overcome gravity and follow a straight path. Instead, orbital transfers are designed to take advantage of gravitational motion by scheduling velocity changes, known as delta-v maneuvers at precise times and places in the orbit.
Procedure
Background
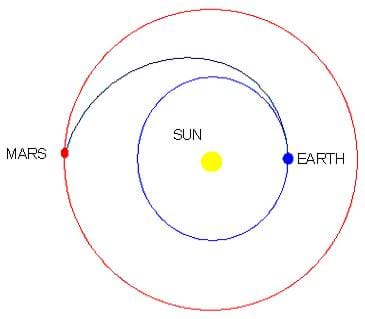
In order to save money on rocket fuel, engineers have designed a way to launch a spacecraft from Earth to Mars that allows the spacecraft to coast and take advantage of the two planets' orbits. This method is called a Hohmann transfer and is a way to transfer from one circular orbit to another circular orbit that is in the same plane (inclination), but a different altitude. This transfer occurs when the launch and arrival points are lined up on opposite sides of the Sun. With the planets in this position, the travel trajectory between them is an ellipse. If the trajectory was from Earth to Mars — like the one of this activity — the ellipse has its perihelion (closest point in to the sun) at the orbit of Earth and its aphelion (furthest point from the sun) at the orbit of Mars.
Before the Activity
- Gather all necessary materials.

With the Students
- Open with a discussion question and a prediction to get students' minds on the activity. First, ask the students how they would go from the Earth to Mars. Brainstorm and encourage wild ideas. Write ideas on the board. Next, ask them if they know how far apart the Earth and Mars are from the sun. Encourage guesses. Tell them they will learn in this activity.
- To draw orbits, we have to scale the actual orbital distance to the size of a paper. The average distance from the sun to the Earth is 149,600,000 km and from the sun to Mars is on average 228,000,000 km. Have the students select a scale (such as: 1 cm = 10,000,000 km) that allows both orbits to be drawn on the paper. Find the orbit radius for the Earth (RE) and Mars (RM) on your scale.
- Ask for a vote from students on the following true or false question: the easiest way to travel between two planets is a direct line. Get a show of hands from students and write the numbers on the board. (Answer: False, it is possible to travel in a straight line from A to B; but in the vicinity of a planet or star, the gravity of the planet or star causes the natural motion of objects to follow an elliptical (or hyperbolic) path. A huge amount of fuel would be needed to overcome gravity and follow a straight path. Instead, orbital transfers are designed to take advantage of gravitational motion by scheduling velocity changes, known as delta-v maneuvers at precise times and places in the orbit. See lesson background information for more detail.)
- Give the materials to the students.
- Tell the students to place a piece of paper on the cardboard and use 4 tacks to hold down the corners. Put one pushpin in the center to represent the Sun. It can be labeled accordingly.

- Cut a piece of thread for the Earth orbit that is 2 times the radius (RE) plus a little extra. Tie the two ends together. The extra length of thread allows for the knot and the extra distance taken up by the pushpin. Do the same for Mars (2 x RM).
- Using the two thread loops and two different colored pens or pencils, draw each orbit around the "Sun" (see figure 3). This is accomplished by putting the loop around the pushpin on one end and the pencil or pen on the other. Make sure the string is pulled tightly all the way around the orbit.
- Now set up the transfer orbit from the Earth to Mars. To do this, you will need to put another pushpin at the focus of the elliptical transfer orbit (see Figure 4). This focus is located at a distance from the Sun equal to the difference between the Mars orbit radius and the Earth orbit radius (RM-RE)
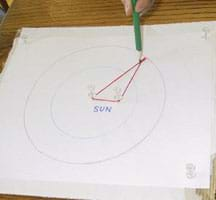
- Use the Mars thread to trace the transfer orbit. Loop the thread around both tacks and the pencil so that the string is in the shape of a triangle as you draw the orbit. Use a different colored pencil to trace the ellipse created by the third string. The orbit should touch the Earth orbit on one side and the Mars orbit on the opposite side.
- Run the post-assessment activity as directed in the Activity Assessment / Evaluation section below.
Assessment
Pre-Activity Assessment
Prediction/Discussion: Ask the students to predict:
- How they would go from the Earth to the Mars.
- How far apart the Earth and Mars are from the sun. (Answer: The average distance from the sun to the Earth is 149,600,000 km and from the sun to Mars is 227,940,000 km.)
- What is an orbit, and why do they exist? (Answer: A natural cyclic motion of one body around a larger body. Consider the moon as an example. Why does the moon circle the earth and not float away? The attraction (force of gravity) of Earth holds it in an orbit around our planet).
Activity Embedded Assessment
Voting: Ask for a vote from students on the following question. Get a show of hands from students and write the numbers on the board for each answer. Discuss the correct answer.
- True or false. The easiest way to travel between two planets is a direct line. (Answer: False, it is possible to travel in a straight line from A to B; but in the vicinity of a planet or star, the gravity of the planet or star causes the natural motion of objects to follow an elliptical (or hyperbolic) path. A huge amount of fuel would be needed to overcome gravity and follow a straight path. Instead, orbital transfers are designed to take advantage of gravitational motion by scheduling velocity changes, known as delta-v maneuvers, at precise times and places in the orbit.)
Post-Activity Assessment
Inside/Outside Circle: Have the students stand in two circles such that each student has a partner. Three people may work together if necessary. The outside circle faces in and the inside circle faces out. Ask the students a question. Both members of each pair think about the question and discuss their answers. If they cannot agree on an answer, they can consult with another pair. Call for responses from the inside or outside circle or the class as a whole.
Define: Ask the students to define the following terms:
- Orbit: The path of a celestial body or an artificial satellite as it revolves around another body.
- Perihelion: The point nearest the sun in the orbit of a planet or other object.
- Aphelion: The point on the orbit of an object that is farthest from the sun.
Discussion Questions: Have students discuss the role of gravity in the motions of the planets and other celestial bodies. Ask them the following questions to guide their discussion:
- What is gravity? (Answer: The attraction between the molecules of one object and the molecules of another.)
- Why does the moon orbit around Earth? Why does Earth orbit around the sun? (Answer: The moon orbits around us because Earth has much more mass (81 times more!) than the moon. We orbit the sun because the sun has much more mass than the Earth (333,000 times more!))
Safety Issues
Make sure students are careful with the pushpins and leave all four upon their desk when leaving the classroom. They should not put the pushpins in their mouths.
Troubleshooting Tips
When tracing the orbits, the students should have enough tension on the string to trace an even, smooth orbit; however, the pushpins might come loose if pulled on too hard. Have one student hold the pushpins down while the second student traces the orbits.
Activity Scaling
- For 6th and 7th grades, do the activity as is.
- For 8th grade, have students draw additional orbits from the sun to other planets.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn how engineers navigate satellites in orbit around the Earth and on their way to other planets in the solar system. In accompanying activities, they explore how ground-based tracking and onboard measurements are performed.

The purpose of this lesson is to teach students how a spacecraft gets from the surface of the Earth to Mars. Students first investigate rockets and how they are able to get us into space. Finally, the nature of an orbit is discussed as well as how orbits enable us to get from planet to planet — spec...

Students explore the outermost planets of our solar system: Saturn, Uranus and Neptune. They also learn about characteristics of Pluto and its interactions with Neptune. Students learn a little about the history of space travel as well as the different technologies that engineers develop to make spa...

Students acquire a basic understanding of the science and engineering of space travel as well as a brief history of space exploration. They learn about the scientists and engineers who made space travel possible and briefly examine some famous space missions.
References
http://www.nasa.gov/home/index.html
http://en.wikipedia.org/wiki/Hohmann_transfer_orbit
http://nssdc.gsfc.nasa.gov/planetary/factsheet/sunfact.html
http://nssdc.gsfc.nasa.gov/planetary/factsheet/moonfact.html
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Penny Axelrad; Janet Yowell; Malinda Schaefer ZarskeSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326.
Last modified: October 13, 2020









User Comments & Tips