Quick Look
Grade Level: 9 (8-10)
Time Required: 30 minutes
Expendable Cost/Group: US $0.00
Group Size: 1
Activity Dependency: None
Subject Areas: Earth and Space, Geometry, Measurement
Summary
Students use vector analysis to understand the concept of dead reckoning. They use vectors to plot a course based on a time and speed. Then they correct the positions with vectors representing winds and currents.
Engineering Connection
Although first described by mathematicians, nearly every branch of engineering uses vectors as a tool today, especially to calculate force and stress. Mechanical, aerospace, civil and chemical engineers who design using fluid dynamics concepts use vectors in their calculations to describe real-world forces such as wind and water movement. Electrical engineers also use them to describe the forces of magnetic and electric fields.
Learning Objectives
After this activity, students should be able to:
- Explain that vectors can represent distances and directions and are a good way to keep track of movement on maps.
- Use vectors to understand directions, distances and times associated with movement and speed.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
(+) Recognize vector quantities as having both magnitude and direction. Represent vector quantities by directed line segments, and use appropriate symbols for vectors and their magnitudes (e.g., v, |v|, ||v||, v).
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
(+) Solve problems involving velocity and other quantities that can be represented by vectors.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
(+) Add and subtract vectors.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Add vectors end-to-end, component-wise, and by the parallelogram rule. Understand that the magnitude of a sum of two vectors is typically not the sum of the magnitudes.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Apply the Pythagorean Theorem to find the distance between two points in a coordinate system.
(Grade
8)
More Details
Do you agree with this alignment?
-
Objects in the real world can be modeled using geometric concepts.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Objects in the plane can be described and analyzed algebraically.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each student needs:
- Vector Voyage Worksheet 1
- Vector Voyage Worksheet 2
- 3 different colored pencils (blue, green and red match the worksheet instructions)
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_navigation_lesson02_activity1] to print or download.Introduction/Motivation
Can you describe speed and distance? (Answer: distance = speed x time; write this on the board.) Remember that for this relationship to work, the units must match. For example, if speed is measured in miles per hour, then time must be converted into hours in order for the answer to be correct.
How did ancient sea captains keep their ships on course throughout their voyages? (See if students have any ideas.) They used dead reckoning to figure out where they were going. Do you think that they followed the sun, the shoreline or even the stars? (Wait for some student responses.) Yes, they did. However, by knowing the speed, time and course of their travel, they could determine where and approximately when they would arrive, which was a great advantage!
Columbus—and most other sailors of his era—used dead reckoning to navigate. With dead reckoning, navigators find their positions by estimating the course and distance they have sailed from known points. Starting from a known point, such as a port, a navigator measures out the course and distance from that point on a chart, pricking the chart with a pin to mark the new position. These early navigators used math to help them find their way and stay on course when wind, current and other factors affected their journeys. Unfortunately, Columbus never reached the destination where he thought he would end up. Why do you think that happened? How accurate is dead reckoning?
Procedure
Dead reckoning is the process of navigation by advancing a known position using course, speed, time and distance to be traveled. In other words, figuring out where you will be at a certain time if you hold the speed, time and course you plan to travel.

The course is the direction you intend to steer the vessel. For this exercise, the "course," or heading, is always due west (270 degrees measured clockwise from 0 degrees north). A heading is which way the vessel is going at a given point. The track actually followed can be very crooked due to wave action, current, wind and the helmsperson (the person responsible for steering the vessel). "Course made good" is the course actually traveled.
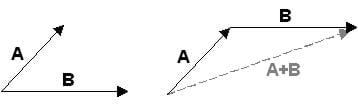
Vectors are arrows that represent two pieces of information: a magnitude value (the length of the arrow) and a directional value (the way the arrow is pointed). In terms of movement, the information contained in the vector is the distance traveled and the direction traveled. Vectors give us a graphical method to calculate the sum of several simultaneous movements. If movement is affected by only one variable (represented by vector A or B), then a vessel would arrive at the end of that vector. If movement is affected by two variables (represented by the sum of A and B), then a vessel's final position can be found by linking the two vectors together.
Before the Activity
- Make copies of the Vector Voyage Worksheet 1 and Vector Voyage Worksheet 2, one each per student.
- Print out the Vector Voyage Worksheet 1, 2 and 3 Answer Keys for yourself.
- Provide students with a brief introduction to vectors.
With the Students
Ask the students: Should sailors worry about wind and current when traveling long distances? (Answer: Yes. Wind and currents can take a ship far from the course it would follow otherwise. If the navigator is not keeping track of the affects of the wind and current, the ship could become hopelessly lost.)
Ask the students: How are vectors related to speed? (Answer: A [velocity] vector tells both speed and direction [N, S, E, W], while speed alone does not tell you direction.)
- Give each student a Vector Voyage Worksheet 1.
- Using the specified color of pencil, have students draw the 10 square movement vectors straight across the map and answer the worksheet questions.
- Have students redraw the 10 square movement vectors on the map while adding the wind vector corrections for each month. Each month's movement vector must start from the end of the previous month's wind vector (refer to Vector Voyage Worksheet 1 Answer Key). Have students answer the worksheet questions.
- Have students redraw the 10 square movement vectors and wind correction vectors on the map while adding the current vector corrections for each month. Each month's current vector now starts from the end of the previous month's wind vector. Each month's movement vector must now start from the end of the previous month's current vector (refer to Vector Voyage Worksheet 2 Answer Key). Have students answer the Vector Voyage Worksheet 2 questions.
- Once they are done, point out how they would have landed on the U.S. without the effects of wind or ocean currents. However, because of wind and ocean currents, they ended up in Cuba.
- Inform students that each square is 100 miles in length. Then have them calculate the distance for Part 1. (Answer: 3,500 miles.)
Vocabulary/Definitions
dead reckoning: The process of navigating by calculating one's current position by using a previously determined position, and advancing that position based upon known or estimated speeds over elapsed time and course.
Assessment
Pre-Activity Assessment
Discussion Question: Solicit, integrate and summarize student responses.
- Should sailors worry about wind and current when traveling long distances? (Answer: Yes. Wind and currents can take a ship far from the course it would otherwise follow.
- Should a navigator pay attention to wind? To current? (Answer: Yes. If the navigator is not keeping track of the affects of the wind and current, the ship could become hopelessly lost.)
Activity Embedded Assessment
Worksheets: As directed in the Procedure > With the Students section, have students complete the activity worksheets and answer the worksheet questions.Review their answers to gauge their mastery of the subject.
Post-Activity Assessment
Student-Generated Questions: Have each student pick a spot on the African coast and then determine the wind and current correction vectors that would take a ship there after 1 month of sailing east 10 squares. Have them exchange these corrections with a partner (without letting the partners see their sheets), and calculate where they would arrive in Africa using their partner's corrections on their own sheets.
Troubleshooting Tips
Getting started drawing vectors may be confusing for students. If necessary, help them by drawing the first two vectors on the chalkboard so the entire class can see, or in small groups.
The wind correction vector is added to the end of the first vector arrow for month 1. The vectors for Part 3 of the worksheets must build off of the added vectors in Part 2. Both the wind and the ocean affect the landfall; this is represented accurately only by building off the wind correction vectors.
Vector Voyage Worksheet 3 Answer Key offers a summary of this activity and clearly illustrates the vector movement directly. This answer key is an excellent teacher reference for students who are having difficulty with this exercise.
Activity Extensions
With students using the Blank Vector Voyage Worksheet, have them plot their own courses, recording movements, directions and corrections along the way. Have them give the new course instructions to a partner to determine if they can sail to the new spot.
Activity Scaling
- For lower grades, do the wind correction part of the activity together as a class. Then have students try the current correction on their own.
- For higher graders, have students calculate the actual total distance traveled by the ship on the way to Cuba. The actual distance traveled by the ship is the resulting vector from the sum of the three movement vectors each month. Students can draw these vectors on their maps by starting at the beginning of the solid 10 square vector for each month and drawing an arrow straight to the final position of the ship for that month. Use the Pythagorean Theorem (a2+b2=c2) to find the lengths of these vectors. (Answer: The distance from Spain to Cuba is 3,683 miles.) Expect students to also be able to calculate the distance from Spain to Florida in the same manner. (Answer: 3,940 miles.)
- For higher grades, have students calculate the speed of the ship in miles per month and miles per hour. (rate = distance/time) (Answer: Florida is 1.37 mph or 985 miles/month, Cuba is 1.7 mph or 1,228 miles/month, and New York is 1.39 mph or 1,000 miles/month.) Are these speeds fast or slow? How about for a ship with no engines? What would happen to the food supply if the ship always encountered a breeze of 6 squares east?
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn that navigational techniques change when people travel to different places — land, sea, air and space. For example, an explorer traveling by land uses different navigation methods and tools than a sailor or an astronaut.

In this lesson, students learn how great navigators of the past stayed on course — that is, the historical methods of navigation. The concepts of dead reckoning and celestial navigation are discussed.

In this lesson, students investigate the fundamental concepts of GPS technology — trilateration and using the speed of light to calculate distances.
Copyright
© 2004 by Regents of the University of ColoradoContributors
Jeff White; Matt Lippis; Penny Axelrad; Janet Yowell; Malinda Schaefer ZarskeSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under grants from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education, and National Science Foundation (GK-12 grant no. 0338326). However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: October 21, 2020








User Comments & Tips