Quick Look
Grade Level: 8 (7-9)
Time Required: 30 minutes
Expendable Cost/Group: US $0.00
Group Size: 1
Activity Dependency: None
Subject Areas: Earth and Space, Geometry, Measurement
Summary
Students learn how to identify the major features in a topographical map. They learn that maps come in a variety of forms: city maps, road maps, nautical maps, topographical maps, and many others. Map features reflect the intended use. For example, a state map shows cities, major roads, national parks, county lines, etc. A city map shows streets and major landmarks for that city, such as hospitals and parks. Topographical maps help navigate the wilderness by showing the elevation, mountains, peaks, rivers and trails.Engineering Connection
Interpreting maps is an essential skill for many types of engineers. Topographic maps include symbols, scales, units and grids — a common language familiar to engineers. Engineering component manufacturing drawings always include this same type of information. For example, some symbols identify important locations on a component, such as its center of gravity. In the drawings, lengths are specified by a consistent set of units. Circuit diagram serve as maps for electrical design; they include unique symbols that communicate to others how to build the circuit.
Learning Objectives
After this activity, students should be able to:
- Convert from one unit of measure to another.
- Understand how scaling works
- Understand how interpreting maps is an essential skill for engineers
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.
(Grade
7)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve problems involving scale drawings of geometric figures, including computing actual lengths and areas from a scale drawing and reproducing a scale drawing at a different scale.
(Grade
7)
More Details
Do you agree with this alignment?
Colorado - Science
-
Describe methods and equipment used to explore the solar system and beyond
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each group (student) should have:
- 1 Topographical Worksheet 1
- 1 Topographical Worksheet 2
- 1 Scale Worksheet
- A pencil
- A calculator
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_navigation_lesson05_activity2] to print or download.Introduction/Motivation
To be able to use a map to find your way, you must first determine where your current location is on the map. You typically do this by comparing the landmarks you see to those shown on the map. You might use a physical landmark like a park or the intersection of two roads. In the U.S., most streets are marked with signs, so finding a street intersection is not too difficult. In some cities around the world, street signs are not very common, so matching up where you are with a point on the map can be tough.
What if you were not traveling to another city but taking a trip in the wilderness? What kind of information do you think that you would need to know? (Possible answers: locations and names of trails, rivers, and mountains.) What if there was a mountain right in the middle of where you wanted to go? Most of us would think to go around the mountain instead of up and over it. How is a map helpful? A map might only show an "X" to indicate the peak (top) of a mountain, but the mountain is large and extends far beyond the actual peak. What would be really helpful would be a map that also tells us how high the mountain is. With such a map, you could determine how big the mountain really is. Luckily, there is a map made just for such purposes: it is called a topographical map.
Procedure
All maps have a scale and a legend. The scale of a map — which is based on the physical size of the map — shows the actual distance between different locations. People can determine this by relating the distance between points on a map (usually an inch) to the actual physical distance between those points on Earth. For example, a scale that might be found on a state map equates one inch to 50 miles.
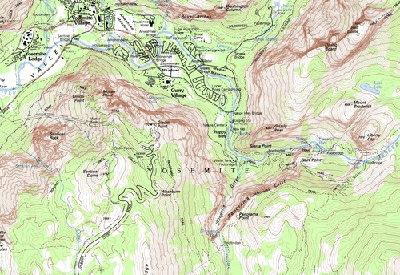
The scale is noted in the map's legend, a set of definitions and background information about what is shown on the map. The legend tells us the name of the area that the map is showing (like which city), the scale (how big the area is), and a list of landmark types and their corresponding symbols (see Figure 1). Common symbols are an X, for peaks, and a Δ (triangle), which denotes a campground. Also shown on the map is its orientation. The orientation tells which direction is north. Most maps (state, road, topographical) show north as pointing straight up. So when we look at a map with the majority of words horizontally readable from left to right, north is always pointing up. City maps are usually oriented so that the layout of the city makes the most sense. If all the roads in a city run northwest to southeast, having a map oriented with north up would make the map look crooked. So, for convenience, a city map for this area would be oriented with northwest toward the top of the page. The orientation arrow still points to north, but it is not pointing up.
Topographical Maps
One frequently-used type of map is called the topographical (or, topo) map. The most important feature of a topo map is that it shows the elevation (or height) of the land using contour lines (see Figure 2). Contour lines connect points around a given area (think of a mountain) that are at the same elevation. Each contour line represents a specific elevation, and on a given map, there is a fixed elevation difference between contour lines. In Figure 2, the innermost circle on the left is marked 40. That means that every point on that line is at an elevation of 40 ft. A closed contour ring like this represents either a peak or a valley — you can tell which one by checking the next few contour lines. In the figure below, the next ring is marked at 30 ft. So, you can see that the 40-ft. contour line encloses a peak with an elevation of at least 40 ft. and not more than 50 ft. (If it is higher than 50 ft., there would have to be another inner ring on the left.) In this picture, you can see that there are actually two peaks — the one on the right goes up to 50 ft. As you move away from the two peaks the terrain levels out so that the 20-foot contour line actually encloses both of the peaks. You can use peaks and valleys on a topo map as landmarks to help identify where you are.
To get a better feel for what is represented by the topo map, we will look at a cross-section of the area. Assume we are interested in going from point A to point B on the map in Figure 2. The cross-section of this path is shown below the contour map, and is known as an elevation plot. The cross-section shows the height of the terrain along the path. You can see from this diagram that traveling directly along the line from A to B would involve going straight up and down the two peaks!
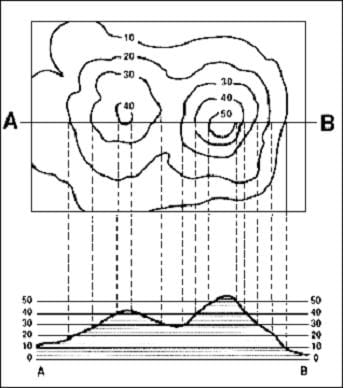
Topo maps are tricky to read at first, but, with a little practice and some helpful tips, reading and understanding them becomes much easier. An experienced map reader can easily spot hills and peaks on the topo map and know, roughly, how difficult or easy it would be walk the terrain. The first thing to notice is the distance between the contour lines. If the lines are far apart, the slope (or elevation change) is small and vice-versa: if the contour lines are close together the slope is greater. The Grand Canyon, known for its high canyon walls, would have contour lines that are very close together. A state like Nebraska, known for its flatness, would barely even have contour lines. This is illustrated in Figure 2. On the left side, the 10-ft. contour line is far away from the 20-ft. contour line. Looking at the same point on the elevation plot, you can see that the slope is pretty shallow. It would be easy to walk up this slope. But, looking at the right hill, the distance between the 40-ft. contour line and the 50-ft. contour line is small. The corresponding elevation plot shows a steep slope. Walking that part of the line would be much more difficult.
Scale, Orientation and Grids
Topo maps use a set of standard scales. This number is a ratio of the distance on the map related to the actual distance. For example, if the ratio were 1:4, an inch on the map would represent 4 inches of actual distance. Of course, this scale would be far too small to be useful, so actual scales are much larger. Below are the three most common scales for topo maps.
- 1:250,000 – These maps cover a large area such as a county or small state. Using this scale, an inch on the map is approximately an actual distance of 4 miles. These maps are useful for long-range exploration.
- 1:62,500 – These maps cover a moderately sized area like a national park. An inch on the map equates to roughly one mile of actual distance.
- 1:24,000 – These maps cover a small sized area. An inch on this map equates to 2,000 ft. This unit of measurement is useful for surveying, so these maps are generally made for this purpose.
The orientation of topographical maps is always north. In other words, north is always pointing up. Topo maps are specifically designed to be used easily with a compass.
Topo maps also have a grid. This grid separates the map into many small square sections. This makes it easier to read the map, to use a compass, and to discuss your location with other people. It is easier to say "I am in grid A5" than it is to say "I am at N40'0.1 by W103'45.6." This grid is made by drawing lines some distance apart that run north-south and then drawing lines that run east-west that same distance apart. This results in a square pattern on the map. These lines are also useful when using a compass.
Before the Activity
- Read through all the steps of the activity.
- Print out Topographical Worksheet 1 and Topographical Worksheet 2 for each student.
With the Students
Part I
- Ask students if they have ever used a topographical map before. What does a topo map look like? How are they helpful? Discuss the features of topographical maps as described above.
- Give each student Topographical Worksheet 1.
- Tell them they have 3 minutes to connect the four pictures.
- When each student has finished, have him or her compare answers with a partner.
- Now have them mark or circle the highest point on each topographical map.
Part II
- Hand out the Topographical Worksheet 2 to each student, and give them each 5 minutes to connect the three pictures.
- When each student has finished, have him or her compare answers with a partner.
- Next, have them mark or circle the highest and lowest point on each topographical map. Give the students 5 minutes to finish the second part of the worksheet.
Part III
- Give each student the Scale Worksheet.
- Ask the students to convert each scale into miles, yards and feet. (You may need to remind students that there are 5,280 feet in one mile.)
- Students will then predict and explain what scales would be best for fitting a classroom, school, or town on a piece of paper.
Assessment
Pre-Activity Assessment
Discussion Questions: Solicit, integrate and summarize student responses.
- Ask students if they have used a topographical map, what one looks like, and how to use it. Discuss the features of topographical maps as discussed in the Procedure section.
Activity Embedded Assessment
Worksheets: Have the students follow along with the activity on their worksheet. After students have finished their worksheet, have them compare answers with their peers.
Post-Activity Assessment
Drawing: Have students depict their subject knowledge gained by drawing a picture.
- Students should draw a topographical map of either their yard or their neighborhood.
Troubleshooting Tips
For the scaling worksheet (Part III), it may be helpful to write the math conversions on the board for students: 1 mile=5,280 ft., 1 foot=12 in., 1 yard=36 in. For advanced students, you may require them to figure out the conversions on their own.
Activity Extensions
Have students can convert to metric (1 km=39370 in., 1 meter= 40 in. (approx)). Using the original scale of 1 in. to X in., students can also calculate what 2 in. would be worth. How about 10 in. or 100 in.?
Out of foam, cut a stack of random, yet increasingly smaller, shapes to represent a hill or landform. Have students trace the foam shapes onto paper, placing the largest shape on the middle of the paper and tracing it, then replacing the shape with the next smallest shape to trace and so on. This activity allows students to use a stack of foam to draw a topographical map — with a resultant drawing that looks similar to an actual topo map.
Activity Scaling
- For 6th grade, have students complete only Part II of "With the Students" in the Procedures section.
- For 7th and 8th grades, conduct activity as is.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn to identify the common features of a map. Through the associated activities, students learn how to use a compass to find bearing to an object on a map and in the classroom.

Students learn that navigational techniques change when people travel to different places — land, sea, air and space. For example, an explorer traveling by land uses different navigation methods and tools than a sailor or an astronaut.

Students learn how to determine location by triangulation. After the process of triangulation is described, students practice finding their locations on a worksheet, in the classroom and outdoors.

In this activity, students learn how to actually triangulate using a compass, topographical (topo) map and view of outside landmarks.
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Matt Lippis; Penny Axelrad; Malinda Schaefer Zarske; Janet YowellSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326.
Last modified: August 10, 2017








User Comments & Tips