Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00
Group Size: 2
Activity Dependency: None
Subject Areas: Earth and Space, Geometry, Measurement
Summary
Students learn about and use a right triangle to determine the width of a "pretend" river. Working in teams, they estimate of the width of the river, measure it and compare their results with classmates.
Engineering Connection
Sometimes engineers cannot directly measure an object's size or distance because it would take too much time, or it is physically impossible (a tape measure to find the distance from the Earth to Pluto?). Instead of actually measuring a size or distance, engineers use trigonometry and other mathematical relationships to estimate it very accurately.
Learning Objectives
After this activity, students should be able to:
- Use right triangle trigonometry and angle measurements to calculate distances
- Convert from US customary to metric units
- Perform averaging and comparison of numbers
- Explain how engineers use trigonometry and other mathematical relationships to estimate distances
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Explain and use the relationship between the sine and cosine of complementary angles.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each group should have:
- Trig River Worksheet
- protractor (or printed copy of the attached Paper Half Protractor)
- 1 piece of string (6-inch long). Any long, very thin items could be substituted, such as spaghetti noodle, pipe cleaner, etc.
- pencil
- tape measure or meter stick (groups can share)
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_navigation_lesson03_activity2] to print or download.Introduction/Motivation
Is it possible to determine the width of a river without crossing it? (Answer: It is possible to come very close to determining the width of a river of any size, using triangles.) The same principle used to determine the width of a river can be applied to other situations, including determining the height of a hill, a tree or a building. The simple geometric shape that makes this all possible is the triangle. During this activity, you will learn how to use triangles to determine the width of a river.
Procedure
Trigonometry is a branch of mathematics dealing with relationships between the angles and sides of triangles. The three basic trigonometric relations that we are concerned with in this activity are: sine, cosine, and tangent (abbreviated as sin, cos, and tan). They are the ratios of the lengths of two sides of a particular triangle. The type of triangle that is most useful to mathematics is a right triangle, which has one angle equal to 90º. By definition, the 90º-angle is made by two lines that are perpendicular to each other (like the corner of a square), and a sloping line connecting the two perpendicular lines makes the third side of the triangle. This sloping line is called the hypotenuse, and the name comes from the Greek hypo (meaning under) and teinein (meaning to stretch). It is easiest to show this visually:
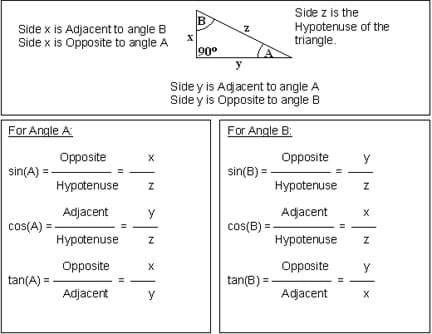
The letters SOH CAH TOA can help students remember which sides go with which functions (Sine = Opposite / Hypotenuse, etc.). Mnemonics may help 6-8th graders memorize the relations: "Some Old Hag Caught A Hippie Tripping On Art" or "Some Oaf Happily Cut A Hole Through Our Apartment."
Before the Activity
- Print out enough Trig River Worksheets for each student and the Paper Half Protractors, if enough protrators are not available for students to use/share.
- Determine whether to conduct the activity indoors or outside.
- Prepare or choose objects that can be used as markers and shore boundaries.
With the Students
Is it possible to determine the width of a river without crossing it? (Allow discussion and entertain any creative ideas: walk through the river, throw a rope across, use stepping-stones, etc. Then state that this river that does not allow solutions those solutions because it is too deep, the current is too swift, it is too wide, you do not have that tool, etc.) If a student knows about using triangles, have them explain as much as they can or introduce the idea and give a quick review of a right triangle — drawing and labeling it on the board.
Define a "river" for the students. For example, if working inside, rearrange desks to form the two "banks" of the river (with space for students to work on each "shore"). If working outside, choose a spot with two widely spaced (2-5 meters) and roughly parallel lines to define the "river" banks. For example, a wide sidewalk, two lines on a football field, or a strip of grass with straight edges. If a small "river" is being measured, have the students measure in centimeters, if a larger "river" is being used, have the students measure in meters. Because these are ratios of distance, the result at the end should have the same unit (meters, centimeters, etc.) used to make the initial measurement.
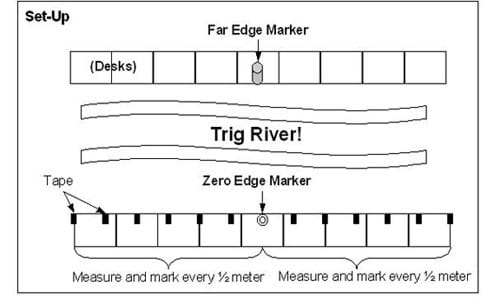
- On one side of the river (as close to the middle of that side as possible, set an object that will be the Far Edge Marker. Normally this represents a tree right at the edge of the opposite side of the river.
- Directly across from the marker, place a Zero Edge Marker (see Figure 1). All the students should be on this side of the river.
- Lay the measuring tape along the "zero edge bank" with one end at the Zero Edge Marker and place a piece of tape every ½ meter on the river edge of the desks. Repeat this in the other direction (see Figure 1).
- Give each student a worksheet.
- Each student should make an estimate of how wide the river is and record it on the back of their worksheet (anywhere on the paper is acceptable).
- Each group will work from a different tape mark. When both students of a group are at their disignated mark and have written on their worksheet the distance their tape is from the Zero Edge Marker, give each group a protractor.
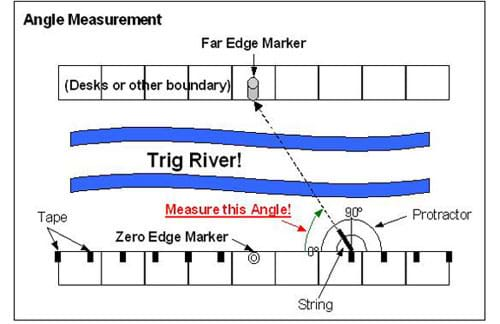
- Lay the protractor with the center point on the middle of the tape and the zero angle pointing toward the Zero Edge Marker (see Figure 2).
- One student will hold the protractor in place while the other places one end of the string on the center point of the protractor and aims the other end at the Far Edge Marker. Read the angle the string passes over on the protractor (counting up from zero; this should not be more than 90 degrees), and record it on the worksheet. While the students do this, the teacher can measure the actual distance between the two markers; do not reveal the distance yet.
- Partners switch jobs and record a second measurement on their worksheet.
- Complete the worksheet calculations. (Leave the desks and markers in place.)
- Have students compare their estimate of the river width to the actual measurement. How close was their estimate?
- Have the students use both metric and English units to measure the distance from the zero marker. Compare the two results at the end.
Question and Answer #1: Were students who were closer to the zero marker more or less accurate than those further away? (Answer: Students close to the zero marker should be less accurate because the values of the tangents of angles close to 90º become large quickly and a small error in the angle measurement results in a large distance error. Note that the same problem would be seen as the measured angle approached zero degrees, but a student would have to be infinitely far away for that.)
Question and Answer #2: Could this measuring method be used in the wilderness if you did not have a calculator or Trig Tables? (Answer: It is not easy to memorize the tangent values for all angles but one value is very easy to remember: tan(45). Have the students find this value and then explain why they get a simple answer.)
Assessment
Pre-Activity Assessment
Discussion Question: Solicit, integrate and summarize student responses.
- Is it possible to determine the width of a river without crossing it? (Allow discussion and entertain any creative ideas: walk through the river, throw a rope across, use stepping-stones, etc. Then state that this river does not allow those solutions because it is too deep, the current is too swift, it is too wide, you do not have that tool, etc.) See "With the Students" in the Procedure section.
Prediction: Have the students estimate how wide the river is and record predictions on the board.
Activity Embedded Assessment
Worksheet: Have the students complete the activity worksheet, Trig Calculations; review their answers to gauge their mastery of the subject.
Post-Activity Assessment
Question/Answer: ask the students and discuss as a class:
- Were students closer to the zero marker more or less accurate than those further away? (Answer: Students close to the zero marker should be less accurate because the values of the tangents of angles close to 90º become large quickly and a small error in the angle measurement results in a large distance error. Note that the same problem would be seen as the measured angle approached zero degrees, but a student would have to be infinitely far away for that.)
- Could this method be used in the wilderness if you did not have a calculator or Trig Tables? (Answer: It is not easy to memorize the tangent values for all angles but one value is very easy to remember: tan(45). Have the students find this value and then explain why they get a simple answer.)
Safety Issues
- Have students use caution not to bump heads when grouping up on taped marks; they may have to take turns if their tape marks are too close for a group of students.
- To avoid tripping over desk legs, remind students to move carefully between the "banks" of the imaginary river.
Troubleshooting Tips
Students may get confused on the trigonometry involved in this activity. After all of the students have tried to figure out the distance across the river, choose one of the tape marks and have the class walk through the activity together for reinforcement.
Activity Extensions
Using the following website, have students complete the navigation example using trigonometry: http://www.staff.vu.edu.au/mcaonline/units/trig/ratios.html.
Activity Scaling
- For lower grades, conduct the activity without step #12 in the Procedure section.
- For upper grades, have students determine the difference between their river estimate and the actual value. Then as a class, plot all the differences (in estimated vs. actual values) vs. the distances from the zero marker. Do the estimates become more or less accurate when measured near or far from the zero marker? Is there an optimal distance from the zero marker that minimizes the error?
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn about trigonometry, geometry and measurements while participating in a hands-on interaction with LEGO® MINDSTORMS® technology. First they review fundamental geometrical and trigonometric concepts. Then, they estimate the height of various objects by using simple trigonometry. Students...

Students learn that math is important in navigation and engineering. They use the Pythagorean Theorem to solve real-world problems.

Students explore the concept of similar right triangles and how they apply to trigonometric ratios. Use this lesson as a refresher of what trig ratios are and how they work. In addition to trigonometry, students explore a clinometer app on an Android® or iOS® device and how it can be used to test th...

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Jeff White; Penny Axelrad; Janet Yowell; Malinda Schaefer ZarskeSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326.
Last modified: May 10, 2022









User Comments & Tips