Quick Look
Grade Level: 11 (9-12)
Time Required: 15 minutes
Lesson Dependency: None
Subject Areas: Geometry, Measurement
Summary
Students explore the concept of similar right triangles and how they apply to trigonometric ratios. Use this lesson as a refresher of what trig ratios are and how they work. In addition to trigonometry, students explore a clinometer app on an Android® or iOS® device and how it can be used to test the mathematics underpinning trigonometry. This prepares student for the associated activity, during which groups each put a clinometer through its paces to better understand trigonometry.Engineering Connection
Some objects and distances in our world are very difficult—even impossible—to directly measure by hand or with tools. Engineers who design different types of structures, either incredibly large or very small, or machines, which might travel distances deep under the sea or far into space, must have an accurate understanding of lengths and dimensions, even when they cannot be measured. Often in these cases, engineers use trigonometry and other mathematical relationships to find very close approximations to lengths and dimensions. In the design of large structures, engineers must ensure that forces acting on the structure will balance so that they remain stationary. Engineers use trigonometry to account for vertical and horizontal components of the different forces that act on structures, thus determining that the structure will be able to stand without collapsing before it is even constructed. These strategies, based on mathematical knowledge, enable engineers to design solutions to problems that might otherwise be unsolvable.
Learning Objectives
After this lesson, students should be able to:
- Describe how a clinometer can be used by engineers.
- Use a clinometer to measure angles.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Use computers and calculators to access, retrieve, organize, process, maintain, interpret, and evaluate data and information in order to communicate.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use various approaches to communicate processes and procedures for using, maintaining, and assessing technological products and systems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
National Council of Teachers of Mathematics - Math
-
use trigonometric relationships to determine lengths and angle measures
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
use geometric models to gain insights into, and answer questions in, other areas of mathematics
(Grades
9 -
12)
More Details
Do you agree with this alignment?
National Science Education Standards - Science
-
Identify a problem or design an opportunity. Students should be able to identify new problems or needs and to change and improve current technological designs.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Nebraska - Math
-
Apply geometric properties to solve problems involving similar triangles, congruent triangles, quadrilaterals, and other polygons.
(Grades
9 -
11)
More Details
Do you agree with this alignment?
-
Identify and apply right triangle relationships including sine, cosine, tangent, special right triangles, and the converse of the Pythagorean Theorem.
(Grades
9 -
11)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/uno_handheld_lesson01] to print or download.Pre-Req Knowledge
Students should have completed a high school course in geometry and understand congruency and similarity in geometric shapes. Students should also have a beginning knowledge of trigonometry.
The teacher must know how to operate the clinometer app for iOS or Android. Most clinometers are self-explanatory with just a little experience. If you use the plaincode clinometer (suggested in the Materials List), it works best to hold the mobile device vertically with 0° displayed at the top of the clinometer, and then rotate the mobile device left or right so that the top or bottom of the device lines up with the sloped side of the angle that you are measuring. The other side of the angle should be aligned horizontally. The degree displayed on the clinometer is the degree measure of the angle. Additional information is provided in the Background Information & Concepts for Teachers section.
Introduction/Motivation
Trigonometry is a branch of mathematics that explores the relationships between the lengths of triangle sides and angles. Engineers routinely use trigonometric concepts to calculate angles. Civil and mechanical engineers use trigonometry to calculate torque and forces on objects, such as bridges or building girders. An example is the calculation of the static forces on an object that is not moving—such as a bridge. The reason a bridge is static (not moving) is because the forces that act on it balance (cancel each other out). Engineers use trigonometry to decompose the forces into horizontal and vertical components that can be analyzed.
Understanding the forces at work on objects is a critical part of statics, which is an essential area of engineering. The study of statics and the related calculations are used by engineers to ensure that buildings and bridges will not collapse due to forces acting on them.
To get started, I'd like everyone to draw two right triangles with congruent corresponding angles (see Figure 1), which implies that the triangles are similar. Similarity is a geometric concept meaning that all corresponding angles are congruent and the ratios of corresponding sides are equal. In layman's terms, similar figures are larger or smaller (scaled) copies of each other. From the geometry concept of similarity, you will extend into trigonometry. 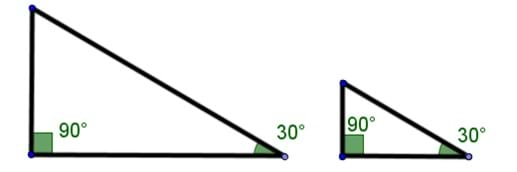
Consider these questions related to your drawn figures:
- What do you notice about the angles of these two triangles? (Answer: The corresponding angles are all congruent.)
- How do you know ALL of the corresponding angles are congruent even though not all are marked as such? (Answer: Since all of the angles in a Euclidian triangle must sum to 180 degrees, and two corresponding angles are already congruent, an explanation using the transitive property or substitution can be made to show the third angles' congruence.)
- How many sides/angles of a right triangle must we know in order to figure out all of the other sides/angles? (Answer: Knowing at least one acute angle and one side allows for discovery of all other parts of a right triangle.)
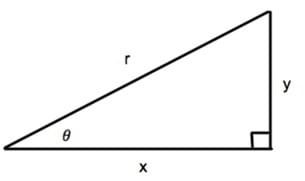
Figure 2. A right triangle
Remember the three trigonometric ratios. (Show students Figure 2 when reviewing the trigonometric ratios, using sides a, b and c, and the acute angle θ to model the relationships.)
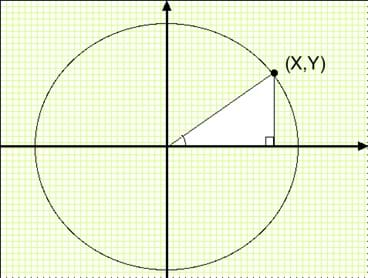
- Sine is opposite over hypotenuse in a right triangle. This means that sin(θ) = y/r.
- Cosine is adjacent over hypotenuse. This means that cos(θ) = x/r.
- Tangent is opposite over adjacent in a right triangle. This means that tan(θ) = y/x.
Why does this work? Think about similar triangles. Remember that the angles are congruent and the corresponding sides are in equal ratios.
Next, take out your Android or iOS device and launch the clinometer app (see Figure 3). Experiment with the app to see what it does. How could this app be used to explore trig ratios? (Many possible answers, but the goal is to lead students to realize that they can measure an angle and the sides of a right triangle and verify that the trig ratios are correct). Refer to the associated activity Trigonometry via Mobile Device for more direction on how to integrate mobile devices with this lesson.

(To sum up the introduction and to get students thinking about the possible applications of trigonometry and clinometers and how they each can be applied to engineering, brainstorm the answers to the following questions as a class.) What types of careers might use trigonometry and clinometers? Where might engineers use trigonometry? For what types of projects might engineers use clinometers?
(Following the discussion, have student pairs use the Internet to confirm their thoughts and/or research other possible answers. When finished, summarize students' results on the classroom board so that the entire class benefits from student research on how engineers use trigonometry and the possible engineering applications of trigonometry and clinometer use.)
Lesson Background and Concepts for Teachers
Similar triangles are the basis for right-triangle trigonometry. Since right angles are congruent, any right triangles that have one other corresponding angle congruent will be similar by geometry's angle-angle similarity postulate. When triangles are similar, the ratios of corresponding sides will be equal. Trigonometry uses this property of similar triangles by calculating the ratios of two sides in a triangle. For instance, sine is the ratio of the side opposite the angle to the hypotenuse in a right triangle. This means that any right triangle with an acute angle of 30° will have the ratio of opposite to hypotenuse of 1:2.
A clinometer is a device that can be used to measure angles. The app on a mobile device allows you to use the mobile device to measure angles. Using the plaincode app with 0° at the top of the clinometer (as shown in Figure 3) you can use either the top or the bottom of the mobile device to measure an angle. By placing the device on a sloped surface and using the clinometer app, the angle of the sloped surface can be read.
Clinometers can be used to measure angles between objects or the tilt of a stationary object, allowing for indirect measurement of distance using trigonometry. The Android or iOS device must be nearly vertical to use the angle measuring function of the clinometer, when it is in the mode matching that of Figure 3. When the clinometer app matches Figure 3, with 0° at the top of the clinometer, rotate the Android or iOS device left or right until the top or bottom of the device matches the sloped side of the angle. The other side of the angle should be aligned horizontally. The degree measure of the angle can then be read from the clinometer. Figure 4 shows the alignment of the clinometer in measuring an angle.
Civil engineers often need to measure very large objects, such as skyscrapers and bridges. It is impractical, and often impossible, to measure these objects with a tape measure. When direct measurements are not possible, technology and mathematics are used instead. Right-triangle trigonometry uses one side of a triangle that is known, combined with a known angle to calculate the other sides of the triangle (which might be the height or length of a building, for example). Engineers use devices such as clinometers to measure the angle required to perform trigonometric calculations.
Various Definitions of Basic Trigonometric Functions
In recognizable terms:
Trig functions are ratios of the legs and hypotenuse of the right triangles used in the Pythagorean Theorem. The basic trig functions are related to the reference angle (the given angle or its equivalent).
In conceptual terms:
If we look at a rectangular coordinate system and place an angle (θ) so that its vertex is located at the origin and the adjacent leg of the angle lies on the abscissa, the basic trigonometric functions of that angle are defined to be:
- Sine – the ratio of the length of the leg opposite the reference angle divided by the length of the hypotenuse.
- Cosine – the ratio of the length of the leg adjacent to the reference angle divided by the length of the hypotenuse.
- Tangent – the ratio of the length of the leg opposite the reference angle divided by the length of the leg adjacent to the reference angle.
In mathematical terms:
The basic trig functions for an angle θ positioned as above are defined, to be:
- sin θ = y/r
- cos θ = x/r
- tan θ = y/x
(Remember from the Pythagorean Theorem that x2 + y2 = r2).
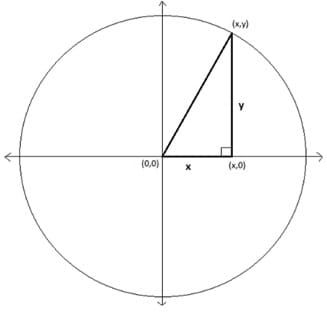
In process terms:
Figure 5 shows a right triangle placed on a coordinate plane with one of its vertices on the origin of the coordinate plane and the center of a circle. One side of the triangle is in the x-direction, begins at the origin and extends a length x. The other side of the triangle is in the y-direction, and extends from the point (x,0) to (x,y). The hypotenuse is of length r and extends from (0,0) to (x,y). Since the trig functions of an angle are defined to be the ratios above, and those ratios do not change based upon the position of the point (x, y) on the hypotenuse, the sine, cosine and tangent are related to the angle θ and not the (x, y) point chosen to calculate the ratios.
Associated Activities
- Trigonometry via Mobile Device - Students investigate the relationships between angles and side lengths in right triangles with the help of materials found in the classroom and an electronic device. Using all or part of a meter stick or dowel and text books or other supplies, students build right triangles and measure the angles using a clinometer application on an Android (phone or tablet) or iOS device (iPhone® or iPad®). Then they are challenged to create a triangle with a given side length and one angle. The electronic device is used to measure the accuracy of their constructions.
Vocabulary/Definitions
clinometer: An instrument for measuring angles of slope, elevation or depression of an object with respect to gravity.
cosine: The ratio of the length of the leg adjacent to the reference angle divided by the length of the hypotenuse.
sine: The ratio of the length of the leg opposite the reference angle divided by the length of the hypotenuse.
tangent : The ratio of the length of the leg opposite the reference angle divided by the length of the leg adjacent to the reference angle.
trigonometry: The study of the relationships between angles and sides of right triangles.
Assessment
Pre-Lesson Assessment
Class Discussion: Ask the class the following questions to gauge their knowledge of trigonometry:
- What do you know about trigonometry? (Example answer: It is a topic of study in mathematics and provides information about the ratios of the sides of right triangles.)
- What tools are available to measure the angle of an inclined surface? (Possible answers: Protractor, level, transit, clinometer.)
- How might you go about measuring the height of a tree or a flag pole? (Example answer: Measure the shadow of the very tall object and measure the angle from the tip of the shadow to the top of the object. Then use the trig function tangent to find the opposite side of the triangle [the height of the object].)
Post-Introduction Assessment
Observations: As students are engaged in the lesson, rove around the room, asking questions and/or observing students working; ask yourself the following (or similar) questions:
- Are students able to explain what the trig ratios are?
- Can students demonstrate that they know how similar triangles are related to trigonometry?
- Do students understand how a clinometer can be used to solve trigonometry problems?
Lesson Summary Assessment
Quiz: Administer the Post-Lesson Quiz to assess students' understanding of trigonometry, clinometers and how engineers use both trigonometry and clinometers in real-world projects.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn that math is important in navigation and engineering. They use the Pythagorean Theorem to solve real-world problems.

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...

Students learn about trigonometry, geometry and measurements while participating in a hands-on interaction with LEGO® MINDSTORMS® technology. First they review fundamental geometrical and trigonometric concepts. Then, they estimate the height of various objects by using simple trigonometry. Students...
Copyright
© 2014 by Regents of the University of Colorado; original © 2013 University of NebraskaContributors
Scott BurnsSupporting Program
IMPART RET Program, College of Information Science & Technology, University of Nebraska-OmahaAcknowledgements
The contents of this digital library curriculum were developed as a part of the RET in Engineering and Computer Science Site on Infusing Mobile Platform Applied Research into Teaching (IMPART) Program at the University of Nebraska-Omaha under National Science Foundation RET grant number CNS 1201136. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.
Last modified: June 13, 2019









User Comments & Tips