Hands-on Activity Trigonometry via Mobile Device

Learning Objectives

After this activity, students should be able to:

• Use a clinometer to measure and explore the angles in right triangles.
• Use trigonometry to find the sides of a triangle given another side and angle.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

Each group needs:

• yard or meter stick (or tape measure)
• sticks or dowels of varying lengths
• 5-6 textbooks or other stackable objects
• masking tape (to hold shapes forming the right triangle in place)
• Android device (phone or tablet) or iOS device (iPhone or iPad)
• clinometer app (available for free from Apple's iTunes store and Google's Play store) such as: Android clinometer: Clinometer (+bubble-level) by plaincode; iOS clinometer: Clinometer HD – bubble level and slope finder by plaincode
• Post-Activity Quiz, one per student

Worksheets and Attachments

Pre-Req Knowledge

Students should have a basic understandingi of trigonometry and know how to run an application on a mobile device.

Completion of the associated lesson, Handheld Trigonometry, to gain an understanding of how to use the clinometer app and learn how trigonometry and clinometers are used in real-world engineering, is strongly recommended. NOTE: Clinometers can be used to measure angles between objects or the tilt of a stationary object, enabling indirect measurement of distance using trigonometry. The Android or iOS device must be nearly vertical to use the angle measuring function of the clinometer. When the clinometer has 0° at the top position, rotate the iPad or Android device left or right until the top or bottom of the device matches the sloped side of the angle. The other side of the angle should be horizontal. Then the degree measure of the angle can be read from the clinometer.

Introduction/Motivation

Have you ever wondered how to calculate the height of a flagpole or a tree fort or the building across the street? Have you ever wondered why bridges or other structures remain standing? Part of the answers to these questions comes from the engineer's application of trigonometry.

Trigonometry is the study of the relationships between angles and sides of right triangles. Civil engineers use trigonometry to help design many structures or to troubleshoot problems. They also use trigonometry to calculate the forces at work on objects so that they understand why something moves or does not move. Aerospace engineers use trigonometry for navigational purposes. The application of trigonometry in so many fields of engineering is a powerful example of how mathematical concepts are vital to engineering design and technology.

Procedure

Background

Student teams explore trigonometry using an Android or iOS device to measure angles. They test their knowledge of trigonometry by experimenting to see if its geometric principles and relationships hold true in the real world. Next, they apply trigonometry and a little engineering design to solve a problem.

Before the Activity

• Prepare the Android and/or iOS devices with a clinometer app.
• Gather the other materials. It is recommended that you provide a variety of stick lengths, so groups are doing calculations different from other groups. Be sure you know the length of each stick, that is, stick A = 8 inches, stick B = 11 inches, etc.)
• Make copies of the Post-Activity Quiz.
• Divide the class into groups of three students each.

With the Students

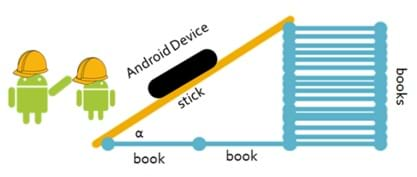
1. To begin, provide each group with a stick of a known length. NOTE: Give each group a different length stick so that each has different calculations.

   

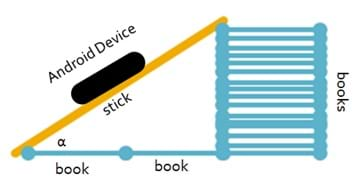
2. Provide each group with a length measuring tool and an Android or iOS device with clinometer app installed.
3. Working in their groups, have students construct right triangles using their stick as the hypotenuse and textbooks or other classroom supplies as the two legs (see Figure 1). Use tape to attach the stick to the book stack so that it does not slip; alternatively, place a heavy object at the base of the stick to keep it from slipping.
4. When you have a right triangle formed, use the mobile device and its clinometer app to measure the angles of the triangle and explore the relationships between the angle measures and the side lengths. The Android or iPad must be nearly vertical to use the angle measuring function of the clinometer. When the clinometer has 0° located at the top, rotate the Android or iPad device left or right until the top or bottom of the device matches the sloped side of the angle. The other side of the angle should be horizontal. Then read the degree measure of the angle from the clinometer. See Figure 2 for more information.
5. After some exploration and practice with the clinometer, inform the teams that they will be given a specific triangle to construct. To accomplish this, students must apply engineering design. Provide each group with a stick of fixed length (this can be a yard or meter stick, or any stick-like object found in the classroom), which represents the hypotenuse of a right triangle. Tell students they can measure this object and use the recorded length in their calculations.
6. Provide each group with a target angle. (NOTE: Assign each group a different acute angle.) The challenge is to create a triangle that has the stick as its hypotenuse and the given angle as one of the acute angles.
7. To begin, have students create a rough draft drawing and calculations of their triangle designs.
8. After a firm plan has been developed, students create polished final drafts of their proposals for the dimensions of the triangle. Require the final drafts to include brief explanations of numerical results.
9. Using their final drafts as a guide, teams build their triangles using a stick and textbooks, blocks, desks or any other teacher-approved classroom objects.
10. Once a group has its right triangle constructed, have the teacher or another student group verify the result using the clinometer app.
11. To conclude, have students write up an explanation of the design process they went through to create their final products. Require the explanation to include final drawing and calculations.

Vocabulary/Definitions

clinometer: An instrument for measuring angles of slope, elevation or depression of an object with respect to gravity.

cosine: The ratio of the length of the leg adjacent to the reference angle divided by the length of the hypotenuse.

sine: The ratio of the length of the leg opposite the reference angle divided by the length of the hypotenuse.

tangent : The ratio of the length of the leg opposite the reference angle divided by the length of the leg adjacent to the reference angle.

trigonometry: The study of the relationships between angles and sides of right triangles.

Assessment

Pre-Activity Assessment

Class Discussion: Ask the class the following questions to gauge their knowledge of trigonometry and how a clinometer works:

• Describe how a clinometer works. (Answer: It measures the angle of an incline.)
• What trigonometric ratios do you know? How do they relate to the sides of a right triangle? (Example answers: The sine of an angle is equal to the opposite side over the hypotenuse. The cosine of an angle is equal to the adjacent side over the hypotenuse. The tangent of an angle is equal to the opposite side over the adjacent side. Each ratio is based on the lengths of the sides of the right triangle.)

Activity Embedded Assessment

Observations: As students are engaged in the activity, rove around the room, asking questions and/or observing students working, and ask yourself the following (or similar) questions:

• Are students effectively communicating using trigonometric vocabulary?
• Are students able to communicate the need for using trigonometry in this situation?
• Do students see the relationship between side lengths and acute angles of a right triangle?
• Is every member of each group playing an effective role in the problem solving process?

Post-Activity Assessment

Quiz: Administer the Post-Activity Quiz to assess students' understanding and ability in applying trigonometric ratios to problems based on a real-life scenario—calculating measurements related to building a radio tower.

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed as a part of the RET in Engineering and Computer Science Site on Infusing Mobile Platform Applied Research into Teaching (IMPART) Program at the University of Nebraska-Omaha under National Science Foundation RET grant number CNS 1201136. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.