Lesson Getting to the Point

Learning Objectives

After this lesson, students should be able to:

• Describe how to use a map and compass to do triangulation and determine their locations.
• Explain bearing measurements.
• Describe how navigation technology plays an important role in many types of engineering design.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Introduction/Motivation

Imagine that you are hiking along a trail in the middle of Rocky Mountain National Park in Colorado. How would you figure out your location? (Listen to student ideas. Possible answers: Look at a map, use a GPS receiver or a compass.) A map gives you information about an area, but it is up to you to figure out how your actual location matches up with what is shown on the map. You can use visual landmarks to help you figure out your approximate location on the map. You can also use a compass to help narrow down where you are in relation to the map.

How would you use a compass to find your location? (Answer: You will have to make measurements to landmarks.)

Now imagine that you are out in the wilderness and you come to the top of a ridge. How can you identify the ridge on the topo map? How can you figure out where you are along the ridge? In today's lesson, we will explore how to use triangulation to answer these questions.

Lesson Background and Concepts for Teachers

Bearing Measurements

The most basic skill in using a compass is taking a bearing. This tells you what direction (or bearing) you are facing or what direction someplace is, like a mountain, tree or building, from where you currently are located. This skill is essential to any activity for which one might use a compass. Simply put, a bearing is the direction to something measured as an angle relative to north. It increases as you turn toward the east, with north=0 degrees, east=90 degrees, south=180 degrees, and west=270 degrees. (Note: Details on using a compass to measure bearing are also described in Lesson 5 of the Navigation unit). Refer to the associated activity Triangulate: Topos, Compasses and Triangles, Oh My! for students to practice the fundamental skills of using a compass. 

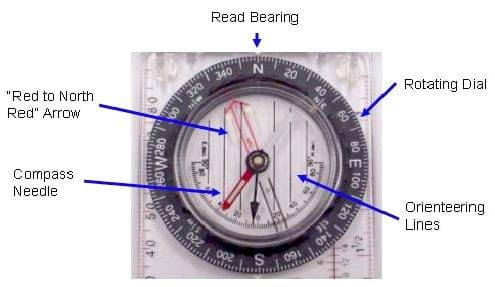
In Figure 2, the black dial shows the bearing angle markings. The bearing will only read out correctly if you have the "N" on the dial aligned with the red arrow (the "Red to North Red" arrow) of the compass needle. After discussing the basics of triangulation, we will discuss a little about correcting for magnetic declination.

Basic Triangulation

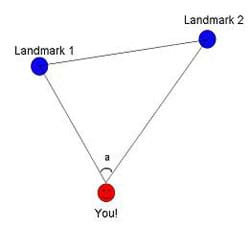
Triangulation is based on finding an unknown location using angle measurements to two known locations. Mathematically, the two known positions define the two vertices (and length of the one side) of a triangle, and the two bearing measurements define two of the angles of the triangle.

These three "knowns" determine the size and orientation of the triangle, thus putting the unknown position at the third vertex of the triangle. In practice, triangulation can be done easily on a map. Refer to the associated activities: Classroom Triangles and Topo Triangulation for students to practice the fundamental skills of triangulation.

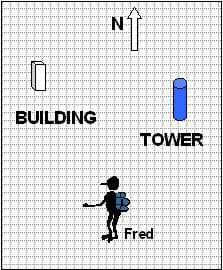
Imagine that you see two landmarks, a building and a tower, at known locations (as illustrated in Figure 3). A lost pedestrian, named Fred, measures the bearing to the tower to be 30 degrees and the bearing to the building to be 345 degrees (see Figure 3). To find his position on the map using triangulation, Fred would draw two lines, one through each of the landmarks beginning where he is standing. The line through the tower should be at an angle of 30 degrees relative to north (as shown in Figure 3), and the line through the building should be drawn at an angle of 345 degrees. His location lies at the intersection of these two lines.

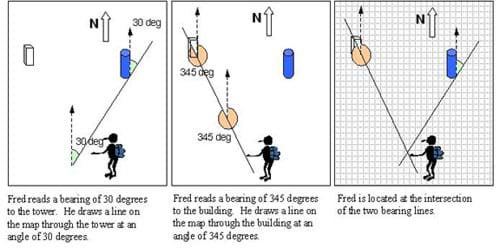
You can use the same approach to find the location of an unknown object by measuring the bearing to it from two known landmarks. For example, we have observers located at the building and the tower. Each measures the bearing to a car at an unknown location. In this example, the bearing to the car measured from the building is 150 degrees, and the bearing to the car measured from the tower is 260 degrees. To find the location of the car, we mark the building and tower locations on the map. Then, through each location we draw a line along the measured bearing as shown in Figure 4. The car must be located at the intersection of the two bearing lines.

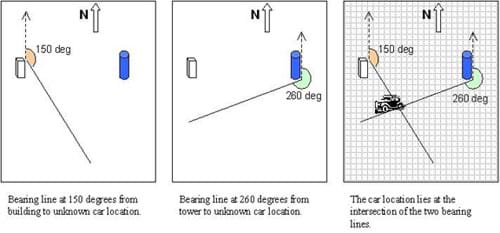
Notice that the bearing measurements can be made at the landmark or at the unknown location. The difference between a bearing from the unknown location to the landmark, and from the landmark to the unknown location is always 180 degrees. That is why you can use the bearing measured at either location to draw the same line.

Triangulation on a Topo Map

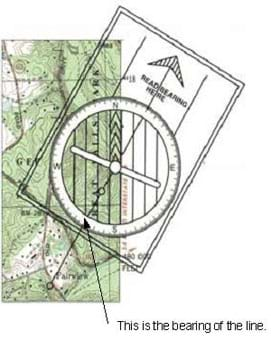
If you are navigating outdoors with the aid of a topo map and a compass, you can apply the triangulation technique to find your location on the map. Using the compass, you take a bearing measurement to two visible landmarks such as hilltops, radio towers or other identifiable sites. A good strategy for triangulation is described below.

First, set the compass up for the bearing to one of the landmarks. To do this, rotate the circle showing the directions until the correct bearing is shown along the arrow. Now, set the compass down on the map so that the long, straight edge lies on the landmark (see Figure 5). Then, rotate the entire compass until the north mark is pointed up on the map (along the vertical lines), keeping the straight edge on the landmark. The arrow points along the correct bearing. Draw a line along the straight edge. Your position lies on this line. Repeat the same procedure for the second landmark. The point at which the lines intersect should be your location.

Correcting for Magnetic Declination

In reality, you must take one more step in order to triangulate on a topo map. When we use a compass to find a bearing with respect to north, we rely on the fact that the geomagnetic North Pole and the geographic North Pole are pretty close to each other. It turns out that the geomagnetic North Pole moves around pretty slowly relative to the geographic North Pole. In 2004, it is located approximately at 82.3° North and 113.4° West (refer to http://geomag.nrcan.gc.ca/index-eng.php for more information).

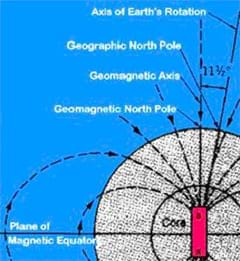
This means that a magnetic compass needle does not point exactly towards geographic north. The angle between geographic and magnetic north at a specific location is known as the magnetic declination.

Topo maps help us make adjustments for this. On a topographical map, near the legend, look for a symbol similar to Figure 7.

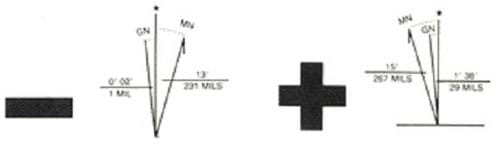
Figure 7 shows the magnetic declination for a map. The sense of the declination describes whether magnetic north is to the east or west of true north. For easterly declinations, a negative sign is shown. For western declinations, a plus sign is shown. These signs indicate how to convert from the true bearing shown on the map to the compass bearing that you would need to follow. For example, in Boulder, Colorado, in 2004, the declination is 10.4 deg East. This means that the direction of magnetic north is 10.4 deg east of true north. If a landmark on the topo map is at a (true) bearing of 10.4 deg, its magnetic bearing is 0 deg (10.4 – 10.4 deg). So, to get there following a magnetic compass you would head off towards 0 deg as shown on your compass. For locations with westerly declination you would add the declination to the true bearing shown on the map to find the magnetic bearing to follow.

When you are using a compass and topo map to find locations by triangulation you have to do the reverse. If you measure the bearing to an object with your compass, you have to add an easterly declination or subtract a westerly declination before drawing the bearing line on your map.

If you are working with a compass and map, two types of adjustments can be made to correct for magnetic declination: temporary and permanent.

Temporary – Work with true bearing on the map, and correct the compass measurements each time. For example, if you want to find your location on the map and you measure bearing using your compass to two landmarks, first adjust the bearing you measured before drawing the lines on the map. If the declination is easterly, add the declination to your reading before drawing the line. A compass bearing of 92 degrees in Colorado would be drawn as a line at 102 degrees on the topo map (92 plus 10). If the declination is westerly, subtract the declination from your measured compass bearing before drawing the line.

Permanent – Some compasses provide a way to make a permanent adjustment, thus eliminating the need to add or subtract the declination. Look for a small screw adjustment on the back of the compass. Turning the screw changes where the red outline arrow points. To permanently adjust the compass, turn the screw until the "red-to-north-red" arrow points to the degree of declination. For example, if our declination is 15 west, turn the screw until the arrow is pointing 15 degrees to the west of north, or 345 degrees (360 minus 15). Figure 8 shows a compass before and after the declination is corrected.

In Figure 8, the left compass shows no declination correction; the red arrow is pointing directly north. The right compass shows a declination correction of 20 degrees west; the red arrow is pointing toward 340 degrees, which is 20 degrees west of north.

Using an Orienteering Compass with a Topographical Map

An orienteering compass is made specifically for use with topographical maps. By using the compass to measure the bearing to two or more landmarks, you can use the basic triangulation and magnetic declination techniques to find your position on a topo map. For instructions on how to determine one's position on a topographical map, see the Lesson Extension Activities section. Students can also use the fun and hands-on associated activity You've Got Triangles! to illustrate how to use simple trigonometry and geometry concepts to estimate and measure the heights of very tall objects. 

Associated Activities

• Classroom Triangles - Students make compass measurements in the classroom to find their locations on a map of the room.
• Topo Triangulation - Students learn how to triangulate with just a map. True triangulation requires both a map and compass, but to simplify the activity and make it possible indoors, the compass information is given.
• Triangulate: Topos, Compasses and Triangles, Oh My! - Students learn how to do triangulation using a compass, topographical (topo) map and view of outside landmarks.
• You've Got Triangles! - With the aid of LEGO® sensor technology, students learn how to use simple trigonometry and geometry concepts to estimate and measure the heights of very tall objects.

Lesson Closure

If you wanted to go somewhere that you have never been to, how could you find your way there? (Expected answer: Use a map.) Are all maps the same size? (Answer: No) What tells us the size of a map and how much area it shows? (Answer: The map's scale.) Where on the map do we find the scale and other important information about the map? (Answer: In the legend.)

If you were planning a wilderness trip, how could a topographical map help you? (Possible answer: It shows the elevation and other interesting features such as mountains, rivers and vegetation.)

If you were lost, could you find your location? (Possible answer: Yes, if you had a map and compass.) What is the method that you could use to find your location? (Answer: Triangulation.)

Vocabulary/Definitions

bearing: The direction in degrees to which an object is located, such as a mountain or tree.

compass: An instrument that uses a magnetized metal bar to indicate the direction of the earth's magnetic poles.

contour line: A line on a topographical map that indicates the elevation along that line.

elevation: The physical height of a location. At sea level this is 0 feet.

legend: A map feature that provides important information about the map, such as the scale, location and landmark symbols used.

orientation: Shows which direction is north on the map.

scale: The ratio of a distance on a map to the physical distance it represents.

topographical map: A map that includes elevation information. Usually used for wilderness travel.

Assessment

Pre-Lesson Assessment

Discussion Question: Solicit, integrate and summarize student responses. Ask the students:

• How could you figure out your location if you were hiking along a trail in the middle of a national park or heavily wooded, mountainous area? (Possible answers: Look at a map, use a GPS receiver or use a compass.)

Post-Introduction Assessment

Discussion Question: Ask the students and discuss as a class:

• Imagine that you are out in the wilderness and you come to the top of a ridge. How can you identify the ridge on the topo map? How can you figure out where you are along the ridge? (Answer: Triangulation, which will be explored further in this lesson.)

Lesson Summary Assessment

Toss-A-Question: With students in groups of two or three students, ask them to independently think of questions formed as a result of the lesson. Have them write the questions on a half sheet of paper. Then have students wad up and toss the paper to a team member who then adds his/her answer idea. If working with three to a group, toss paper to third group member to add her/his answer below the questions. After all students have written down ideas, have them toss the paper to another team, who reads the question/answers aloud to the class. Discuss answers with the class. Refer to the Lesson Closure section for question ideas.

Homework

Map Quest: Assign students to search libraries, homes and/or the Internet to find topographical map examples. Ask them to each bring one to share with the class during the next class period.

Lesson Extension Activities

Have students determine their positions on a topographical map. Topo maps can be obtained in advance free of charge from the US Geological Survey or purchased at most outdoor equipment stores.

1. Determine your declination. Either correct this permanently or just find it to be used later.
2. Find two landmarks on the map that are easily identifiable. Antenna towers or big mountains usually work best (see Figure 9).

3. Find those landmarks outside, and take their bearings with your compass. Write these down on the map, possibly next to the landmark on the map. Make sure to correct for declination. If you permanently adjusted your compass, then this is already corrected for you, but if you only did the temporary adjustment, add or subtract that to your bearings.
4. Do the same for the second landmark.
5. These two lines should intersect. You are (more or less) at the point where they intersect. Now you know where you are!
6. To get a more accurate location, measure a bearing to a third landmark. With three landmarks, the bearing lines do not all intersect at a single point, but their intersections forms a small triangle. Your location is within this triangle.

References

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the NSF and you should not assume endorsement by the federal government.