Hands-on Activity Close Enough? Angles & Accuracy of Measurement in Navigation

Learning Objectives

After this activity, students should be able to:

• Understand that navigation is based on mathematics
• Understand accuracy and precision
• Use right triangle trigonometry and angle measurements to calculate distances
• Understand the relationship between triangulation technology and other fields of study (i.e. mathematics)

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

Each student should have:

• 1 each Accuracy By Hand Worksheet
• pencil

Class will share:

• 3 different colored markers
• 1 piece of string or rope, exactly 10 meters long (use one color to mark the zero point and other colors to mark the 6 and 8 meter points)
• 10-15 small cups to use as markers
• calculators (students may use a Trig Table instead, if calculators are unavailable)
• tape measure or meter stick
• protractors (or copies of Paper Half-Protractor)
• masking tape

Worksheets and Attachments

Introduction/Motivation

Ask the students how accurately things have to be measured. (Answer: It depends on what is being measured.) Should everything be measured down to the millimeter? Can all measurements be rounded off to the nearest foot? Explain that the needed accuracy of a measurement depends on what is specifically being measured (for example, a length of thread vs. a post to build a fence). When navigating, how accurately do we need to measure an angle? (Answer: Again, it depends on how precise you need to be based on what is being navigated.) In this activity, we will investigate how precise measurements need to be to find an Invisible Island.

Procedure

Accuracy and Precision in Measurement

There are two basic concepts to any collection of measurements, accuracy and precision. Accuracy is how close the measured data is to the actual value. For example, if you know that you have a mass standard that is 50.00 grams, and you measure it to be 49.98 grams, then your measurement is very accurate. On the other hand, if you measure it to be 43.24 grams, your measurement is not very accurate.

Precision is how close your measurements are relative to each other, not the actual value. For example, let say you measured that same mass standard and came up with the values:

43.24, 43.30, 43.20, 43.25, 43.32

You could say that your measurement was very precise because all the values are very close to each other. On the other hand, if your measurements were:

50.03, 43.40, 53.01, 47.54, 30.23

Your measurements would not be very precise because they are all far apart relative to each other.

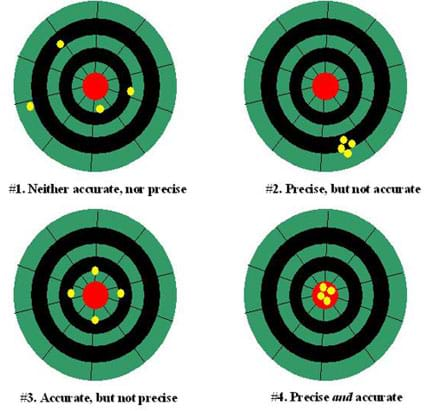
A dartboard is a common example of showing the difference between accuracy and precision (please see Figure 1). Assume that someone throws four darts at a dartboard. If they are far apart and unevenly spaced, they have neither precision nor accuracy (#1). The closer the darts are to the center, the better accuracy they have. The closer the grouping of darts is to one another, the better precision they have (#2). If the darts are evenly spread around the center, the dart thrower has low precision but high accuracy — they are not close to each other but all of the darts are equally far from the center (#3). And finally, if all of the darts are closely grouped in the center of the dartboard, the thrower has both high accuracy and precision (#4) because the darts are either on or very close to the target.

Trigonometry

Trigonometry is a branch of mathematics dealing with relationships of the angles and sides of triangles. The three basic trigonometric relations that we are concerned with — sine, cosine and tangent — are ratios of the lengths of two sides of a particular triangle. A very useful type of triangle is a right triangle, which has one angle equal to 90º. By definition, the 90° angle is made by two lines that are perpendicular to each other (like the corner of a square), and the third side of the triangle is made by a sloping line connecting the two perpendiculars. This sloping line is called the hypotenuse, and the name comes from the Greek words hypo (meaning under) and teinein (meaning to stretch). Essentially, hypotenuse means to stretch under the 90° angle. It is easiest to show this visually.

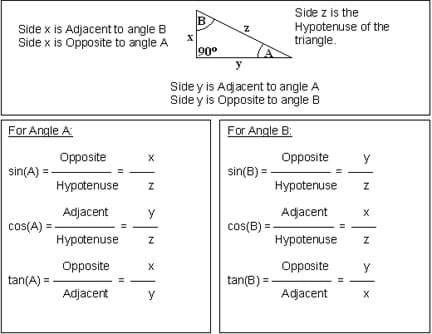
The letters SOH CAH TOA can effectively help students remember which sides go with which functions (Sine = Opposite / Hypotenuse, Cosine = Adjacent/Hypotenuse, etc.). Mnemonics may help students memorize the relations: "Some Old Hag Caught A Hippie Tripping On Art" or "Some Oaf Happily Cut A Hole Through Our Apartment."

Before the Activity

• Make enough copies of the worksheet, trig table, and paper protractor (if needed).
• Determine whether the activity will be performed indoors or outside. A space that has as least a 10 meter square of floor/ground space is needed.
• Measure and mark string or rope (see materials list).

With the Students

1. Give each student an Accuracy By Hand Worksheet.
2. Have students use calculators to do the "Sailing to an Island" and the "Rocket to the Moon" problems on the worksheet.
3. Help students answer the question on the bottom of the worksheet: Why must the rocket to the moon be more accurate than sailing to an island? (Answer: Because the target is smaller relative to the distance traveled than the island is.) This can be seen by looking at the ratio of the size of the target and the distance to it: Island = 50/1000 = .05 and Moon = 1738/382700 = .0045.

Now the students will try this in real life. Explain that you have a navigation mission for them that requires accuracy of measurement. They are going to locate an Invisible Island.

1. Divide the class into teams of two and hand out markers (small cups with tape on them so students can mark their names. If outside, some sort of weight should be added to cup: gram weights, rocks, etc.)
2. If outside, take string/rope and masking tape with you.
3. Take students to the "test" area (field outside, gym, or large enough classroom).
4. Choose a natural straight line (edge of field, sidewalk, line in gym, or even a wall will work) that is at least 8 meters long (25 ft.). Mark the start point with an "X" of tape or object that can be stuck into the ground (a pencil) and place the protractor on the start point (see below).

Tell students that the Invisible Island is located exactly 10 meters away and 37º off of the baseline from the start point.

Note: Students should wait in line to have their turn.

5. One partner will line up the protractor at a 37º angle and hold the zero end of the string at its center point. The other partner, carrying a labeled team cup, will take the end of the string and walk out at a 37º angle until the rope is tight. When both partners think they are close to having the final position at a 37º angle from the baseline, the cup is set down.
6. Have each group take turns placing their cup where they think the island is located. Caution each group not to just put their cup by another groups, as they could wrong.

Once all groups have placed their cup, reveal the location of the Invisible Island:

1. Use the marked string to measure exactly 8 meters along the baseline from the start point and mark this spot with masking tape.
2. Use the protractor to measure a 90º angle at this spot.
3. Use the string to measure exactly 6 meters along this line (see below), perpendicular to the baseline toward the cups. Mark this spot as the island.

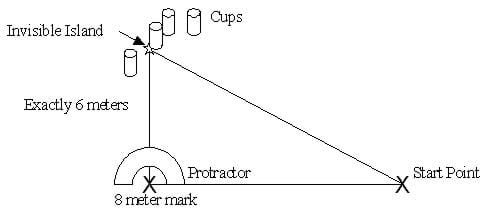
4. Use a meter stick or tape measure to measure the distance of each cup from the actual island location. Rrite the distance on the tape on the cup.
5. Have the teams return to the classroom with their cups.
6. Have the students look at their Accuracy By Hand Worksheet again and notice that the numbers for the "Sailing to an Island" problem are similar to the ones just used: Instead of the island being 1000 km away, the invisible island was 1000 cm away (there are 100 cm in a meter so 10 x 100 =1000cm). From this information, have them estimate how far off their angle measurement was.
7. Run Numbered Heads post-assessment activity with the students as directed in the Assessment & Evaluation section.

Assessment

Pre-Activity Assessment

Discussion Question: Solicit, integrate, and summarize student answers.

• Ask the students how accurately things have to be measured. (Answer: It depends on what is being measured.) Should everything be measured down to the millimeter? Can all measurements be rounded off to the nearest foot? Explain that the needed accuracy of a measurement depends on what is specifically being measured (for example, a length of rope vs. a post to build a fence). When navigating, how accurately do we need to measure an angle? (Answer: Again, it depends on how precise you need to be based on what is being navigated.)

Activity Embedded Assessment

Worksheet: Have the students complete the activity worksheet; review their answers to gauge their mastery of the subject.

• Accuracy calculations: Students should follow and complete the attached worksheet.

Post-Activity Assessment

Numbered Heads: Break the class up into teams of three to five. Students on the team should pick numbers so each member has a different number. Ask the students a question (give them a time frame for solving it, if desired). The members of each team should work together on the question. Everyone on the team must know the answer. Call a number at random. Students with that number should raise their hands to answer the question. If not all the students with that number raise their hands, allow the teams to work on the question a little longer.

• Question: Why was it hard to get the angle right to find the Invisible Island? (Answer: Several possible reasons: the string or rope was much thicker than the divisions on the protractor, the protractor only had divisions of 5 degrees, it was hard to get the string tight, it was hard to keep the protractor lined up, etc.)
• Question: What would need to be done to get as close as only a kilometer away from a marked spot? (Answer: A more accurate angle measurement would need to be made, and the easiest method would be to use something like a 5-foot long protractor that showed divisions down to the 1/100 of a degree. Finding a rope this long would be a problem though.)

Safety Issues

Since this activity requires a large space to complete, be sure to find an open, unpopulated area to use (at least a 10 meter square of ground or floor). Otherwise, the students may run into a wall, desk, playground equipment or other students, which ultimately could cause an injury if students are not careful.

Troubleshooting Tips

If a large, open area is not used, students may not be able to find the Invisible Island due to obstructions.

This is a great springboard for vectors; go over vectors with the class using a chalkboard protractor.

The team activity works better on a flat surface, such as a gymnasium floor or blacktop play area, rather than on grass.

For younger students, a large protractor or chalkboard protractor is easier to measure the angle of the string.

Activity Extensions

Work the Invisible Island km vs. cm equation backward to find how far off the angle the teams were (when they placed their cup on the spot they thought was the Invisible Island). This will require using the "arcsin" or "inverse sin" function on a calculator.

Activity Scaling

• For 6th grade, use or make a fairly large protractor (photocopier enlargement is an option) so that students can more easily find the angle.
• For 7th grade, do the activity as is.
• For 8th grade, have students use a compass to stay on the correct angle until the string is tight.

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326.