Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00 (assumes students have protrators)
Group Size: 1
Activity Dependency: None
Subject Areas: Earth and Space, Geometry, Measurement
Summary
Students learn that math is important in navigation and engineering. They learn about triangles and how they can help determine distances. Ancient land and sea navigators started with the most basic of navigation equations (speed x time = distance). Today, navigational satellites use equations that take into account the relative effects of space and time. However, even these high-tech wonders cannot be built without pure and simple math concepts — basic geometry and trigonometry — that have been used for thousands of years.
Engineering Connection
Understanding the properties of certain shapes is useful to engineers. For example, to measure extremely long distances, engineers use their understanding of geometry and angles. Civil engineers sometimes design buildings with cross-bracing for added strength. Depending on the type of cross-bracing used, different triangle shapes are formed, which greatly affects the structure quality. Computer engineers who design recordable compact discs to store music calculate the disc's circumference (circle perimeter) to determine its storage capacity.
Learning Objectives
After this activity, students should be able to:
- Describe how navigation technology is founded on mathematical principles that have been used for thousands of years
- Use geometric relations of triangles and circles to find distances.
- Use the Pythagorean Theorem.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
(Grade
8)
More Details
Do you agree with this alignment?
-
Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
(Grade
8)
More Details
Do you agree with this alignment?
Colorado - Science
-
Describe methods and equipment used to explore the solar system and beyond
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each student needs:
- pencil
- protractor (can share among students)
- Stay in Shape Worksheet
- Stay in Shape Datasheet
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_navigation_lesson03_activity1] to print or download.Introduction/Motivation
How important is understanding shapes and angles when navigating? (Answer: Very important: being able to determine a position relative to other objects depends on knowing geometric relationships.) As the world grows more complex, we want to navigate faster and know exact distances and times of travel.
How did people first determine distances between cities? Or, how about the size of the Earth? (Answer: They measured the distance between two cities and then used trigonometry to extrapolate that to the size of the earth.) It is all possible using relationships of simple shapes and angles. These principles can be applied to determine almost any distance or height given appropriate reference points. Triangles and their usefulness for measuring distance will be explored in this activity.
Procedure
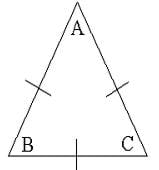
The sum of the angles in any triangle is 180º.
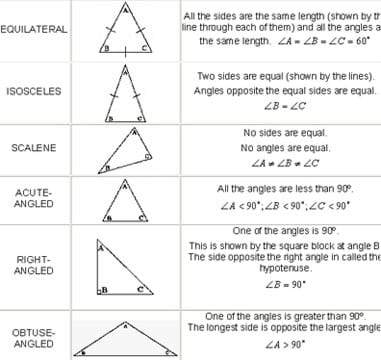
Types of triangles:
Pythagorean Theorem was an idea discovered by Pythagoras, a Greek mathematician who lived from 569-500 BC. It is said that he discovered the special property of right-angled triangles while looking at the tiles of an Egyptian Palace.
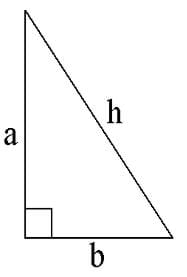
Pythagoras said, "In a right angled triangle, the area of the square of the hypotenuse equals the sum of the squares of the other two sides."
h is the hypotenuse
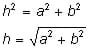
A radian is the angle made when the radius of a circle projects an arc on its perimeter.
One radian is the measure of the angle created at the center of a circle by an arc on the perimeter equal in length to the radius of the circle. A radian is a different way to measure an angle than using degrees.
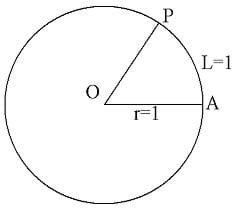
If r = 1 unit
and length, L = 1 unit
then ∠AOP = 1 radian
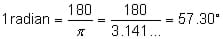
1 radian = 57.30 degrees
If there are 360º in a circle, then 360º / 57.3º per radian = 6.28 radians on the perimeter of a circle. Notice that number equals 2 x 3.14 (pi or π) radians; therefore, 3.14 radians = 180º.
Before the Activity
- Print out enough copies of the Stay in Shape Worksheet and Stay in Shape Datasheet, one each per student.
- Review the properties of triangles and circles, as described above.
With the Students
Remind students that understanding shapes and angles is important in navigation; being able to determine a position relative to other objects depends on knowing geometric relationships. Explain that the word "geometry" comes from the Latin roots geo (meaning land or Earth) and metry (meaning measure). Geometry, therefore, means measurements of the Earth, which is precisely what is needed in navigation.
- Have students brainstorm in groups what they know about triangles and circles. Clarify the true statements and write them on the board.
- Hand out the worksheets and datasheets
- Do the the Ship #1 problem as a class. Have the students try the second ship problem on their own. Note: It may be helpful to write the following chart on the board for the Ship #2 problem. First write the numbers 1-15 across and then have the students come up with the square values for each.

- Do the third ship problem with the class. (For question #3, the relationship between a circle's radius and its perimeter must be established. Discuss what this relationship is from the background section.)
- Ask the students to add any new properties of triangles and circles learned to the list already on the board.
Assessment
Pre-Activity Assessment
Brainstorming: In small groups, have students engage in open discussion. Remind students that no idea or suggestion is "silly."
- What are the properties of triangles and circles? Write on board as directed in Step 1 of the "With the Students" section.
Activity Embedded Assessment
Shape Datasheet and Shape Worksheet: Have students complete the attached worksheets.
- Have students do geometry calculations on the data sheet of angles and distances.
Post-Activity Assessment
Debrief: Lead a discussion on the learned subject and ask students to relate their observations of the activity.
- Ask for input from students to add new — or remove any proven false — properties of triangles and circles learned to the list already on the board.
Troubleshooting Tips
If students get confused when working on the circular question (#3) of the third ship problem, clarify the difference between radians and degrees (that is, what does it mean to be 50 radians away?). Use the worksheet as a teaching tool.
Activity Extensions
Using the website: http://www.staff.vu.edu.au/mcaonline/units/trig/trigraddegrees.html, either as a group or individually, have students complete some of the sample problems.
Activity Scaling
- For younger students, work through all the activities together.
- For older students, discuss why the curve of the Earth was not used in the first and second ship problems. (Answer: Because the distances were very small compared to the curve of the Earth. At small distances the Earth can be considered flat.) At what distance is it necessary to include the curve of the Earth? (Answer: It depends on the application and how accurate the measurement needs to be. But, if you were sailing to an island using a flat Earth map, you would be short of your target by about 5 miles after sailing 100 miles (probably within sight on a clear day). If the island were 1,000 flat miles away, you would end up being 50 miles short.

Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students learn that math is important in navigation and engineering. They use the Pythagorean Theorem to solve real-world problems.

Students explore the concept of similar right triangles and how they apply to trigonometric ratios. Use this lesson as a refresher of what trig ratios are and how they work. In addition to trigonometry, students explore a clinometer app on an Android® or iOS® device and how it can be used to test th...

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...

Students learn about trigonometry, geometry and measurements while participating in a hands-on interaction with LEGO® MINDSTORMS® technology. First they review fundamental geometrical and trigonometric concepts. Then, they estimate the height of various objects by using simple trigonometry. Students...
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Jeff White; Matt Lippis; Penny Axelrad; Janet Yowell; Malinda Schaefer ZarskeSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326.
Last modified: December 15, 2021









User Comments & Tips