Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00
Group Size: 2
Activity Dependency: None
Subject Areas: Earth and Space, Geometry, Measurement
Summary
In past times, ocean navigators tossed a piece of wood over the side of their ships and noted how long until the ship passed the wood. They used this time measurement and the length of the ship to calculate their speed and estimate how far they had traveled. In this activity, students act the part of a GPS signal traveling to the receiver to learn how travel time is converted to distance.
Engineering Connection
Our world is quickly becoming wireless. Remote controls, cell phones, laptops and GPS technology use wireless signals of various types. Electrical and computer engineers create wireless technology and equipment that sends and receives information through the air. They also decide what kind of information to transmit. In the case of GPS, time information is send and later converted to distance information via mathematical calculations.
Learning Objectives
After this activity, students should be able to:
- Examine error propagation (time delay).
- Understand that GPS distance is determined by knowing the time it takes a signal to travel from a satellite to the receiver and multiplying that time by the speed of light. They should learn that a delay in the signal's travel will increase the time and make the receiver think the satellite is farther away.
- Describe the effects of the atmosphere on GPS receiver error
- Understand early navigation technologies and how advancements in technology have improved our ability to navigate
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Fluently divide multi-digit numbers using the standard algorithm.
(Grade
6)
More Details
Do you agree with this alignment?
-
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association.
(Grade
8)
More Details
Do you agree with this alignment?
-
Use the equation of a linear model to solve problems in the context of bivariate measurement data, interpreting the slope and intercept.
(Grade
8)
More Details
Do you agree with this alignment?
-
Represent data on two quantitative variables on a scatter plot, and describe how the variables are related.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Communication systems are made up of a source, encoder, transmitter, receiver, decoder, and destination.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Engage in a research and development process to simulate how inventions and innovations have evolved through systematic tests and refinements.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities.
(Grade
8)
More Details
Do you agree with this alignment?
-
For scatter plots that suggest a linear association, informally fit a straight line, and informally assess the model fit by judging the closeness of the data points to the line.
(Grade
8)
More Details
Do you agree with this alignment?
Colorado - Science
-
Describe methods and equipment used to explore the solar system and beyond
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each group should have:
- 1 stopwatch or timekeeping device that can count seconds
- 1 It's About Time Worksheet
- A pencil
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_navigation_lesson08_activity2] to print or download.Introduction/Motivation
We know that early navigators had to rely on very archaic tools to determine their speed and course. Since that time, engineers have developed very sophisticated devices to help with navigation. However, do the methods used in early times apply to today? Would the same basic idea of early navigators using a piece of wood thrown overboard at the front of their ship and then counting until the wood passes a mark near the back of the ship to determine their ship's speed work for the signals of a satellite navigation system? Absolutely; in fact, it works better because we already know the speed of the satellite signal is the speed of light — a constant. Working with a constant is far better than working with something unknown.
Navigation satellites are like orbiting landmarks. Rather than seeing these landmarks with our eyes, we "hear" them using radio signals. GPS, or Global Positioning System, is a constellation (or set) of at least 24 satellites that continuously transmit faint radio signals toward the earth. These radio signals carry information about the location of the satellite and special codes that allow someone with a GPS receiver to measure distance to the satellite. By combining the distances and satellite locations, the receiver can find its latitude, longitude, and height. In this activity, you will learn how travel time is converted to distance.
Procedure
The Global Positioning System – GPS
GPS satellite signals are free and available for anyone to use. GPS receivers are decreasing in cost every year and can be found in sporting good, or discount stores, and in fact, are even embedded in cell phones and watches.
GPS is based on satellite ranging. Our position on earth is calculated by measuring our distance from a group of satellites in space. This process, called trilateration, is done by timing how long it takes a radio signal to reach us from a satellite. The signal travels at the speed of light (186,000 miles per second), so we are able to calculate the distance using: Velocity x Time = Distance. If the signal is delayed for even 1/1000th of a second, the distance will be off by 186 miles.
So, how do we know where the satellites are? (Answer: All satellites are constantly monitored.) They have a 12-hour orbit, and the U.S. Department of Defense is able to monitor the satellites from ground stations around the world. The satellites are checked for errors in their position, height, and speed. These minor errors are caused by gravitational pulls from the moon, sun, and even pressure from solar radiation on the satellite. The satellites transmit special codes for timing purposes, and these codes carry a data message about their exact location. This helps to locate the satellite precisely.
There can be errors in reading a GPS location because of various reasons. The Earth's ionosphere and atmosphere can cause delays in the signal, which make the distances seem longer than they should be. The ionosphere is a blanket of electrically charged particles 80 to 120 miles above the earth and the atmosphere can have varying amounts of dust, water vapor (clouds), and other particles floating around.
How else can the signal be slowed down? Picture the signal coming into a raindrop at an angle; it travels slightly slower through water than air. The left edge of the signal wave encounters the raindrop first, and slows down. The point of the signal just to the right travels a bit farther at the higher speed, but then it encounters the material also, and slows down. This happens all along the wave. The signal can be refracted and reflected as it goes though a raindrop that scatters parts of the wave and weakens the signal.
Satellite clock errors, receiver errors on earth, and signal reflection can also cause errors in final position. In 2002, a typical receiver could tell you your latitude and longitude to within 20 ft.
Before the Activity
- Print out enough worksheets for each group of students.
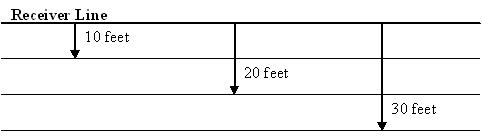
- In an area, such as a playground, field, or gymnasium where the students can run (or make them speed walk if you prefer), mark off four parallel lines using masking tape. The first line is where the "receivers" will sit facing away from the other lines. Each receiver should have enough space that they can reach out toward their neighbors and not touch. The first line behind the receiver line should be 10 feet away. The next, 20 feet from the receiver line. And the last line should be 30 feet away from the receiver line.
With the Students
- Run the Voting assessment as directed in the Assessment / Evaluation section.
- Give each group an It's About Time Worksheet.
- When the students have decided who is the first "receiver" (or decide for them), give that student a stopwatch (or other time device that counts seconds).
- Take the students to the lined area and have them follow and record their data on the worksheets.
- Have students plot the data with the X-axis being time and the Y-axis being feet. (These three data points may not be linear. If not, have students estimate a line of best fit.)
- Have students make predictions on how much time it would take for the "signal" to travel 15, 25, 50, and 100 feet.
- Ask Question/Answer assessment and give the survey as directed in the Assessment / Evaluation section.
Assessment
Pre-Activity Assessment
Voting: Ask a true/false question and have students vote by holding thumbs up for true and thumbs down for false. Count the votes, and write the totals on the board. Give the right answer.
- In the old days, ocean navigators used to throw a piece of wood over the side of the ship and count off the time it took the wood to be passed by the ship. They would then use this time and the length of the ship to calculate the speed of the ship to get an estimate of how far they had traveled. Would this same basic idea work for the signals of a satellite navigation system? (Answer: Absolutely. In fact, it works better because we already know the speed of the signal is the speed of light — a constant.)
Activity Embedded Assessment
Worksheet Calculations: Have the students complete the activity worksheet; review their answers to gauge their mastery of the subject.
Post-Activity Assessment
Question/Answer: Ask the students and discuss as a class:
- Is it possible for the signal to arrive earlier than expected? (Answer: Not if the satellite is in the orbit you think it is in: the speed of light is absolute and cannot be exceeded. However, if the satellite's orbit were closer than you think it is, the signal would seem to arrive early. Hopefully you are locked into enough other satellites' signals to know that this one has an error.)
Survey: Ask the following questions (verbal or written) to survey students about the activity.
- What did you like best about this activity?
- What did you learn from this activity?
- How could this activity be improved?
Troubleshooting Tips
The graph that students make will probably be quasi-linear (it will not make a straight line). Have students make a line that comes closest to all three of them (a line of best fit).
Activity Extensions
Have students figure out what the average travel time is for a GPS signal if the orbit is 20,000 km and the Earth's radius is about 7,000 km. (Answer: 13,000 km at 300,000,000 km/sec = 0.000043 seconds.)
Activity Scaling
- For 6th and 7th grades, do activity as is.
- For 8th grade, once students have gotten the hang of the activity, have them all sit in a very large circle facing in, with a wall or obvious landmark in one or more directions. Have one student volunteer to be the "receiver" and then pick three students spaced around the circle to stand up and be "signals." The receiver will be able to look at where the three signals are standing but will then be blindfolded. The receiver will then be taken in a round about way (be careful not to make them dizzy) to a random spot in the circle and sat down. When ready, the receiver yells "GO!" The signals all run to the receiver as directly and quickly as possible saying "Here!" when they arrive. The goal of the receiver is to determine from the arrival times of the signals, roughly where they are in the circle. Unlike a normal receiver, the student will have the advantage of hearing the direction of the signal's arrival. Can they also figure out which way they are facing?
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

In this lesson, students investigate the fundamental concepts of GPS technology — trilateration and using the speed of light to calculate distances.

During a scavenger hunt and an art project, students learn how to use a handheld GPS receiver for personal navigation.

Students explore the concept of triangulation that is used in navigation satellites and global positioning systems designed by engineers. Also, students learn how these technologies can help people determine their positions or the location of someone else.

In this lesson, students explore the role of communications and how satellites help people communicate with others far away and in remote areas with nothing around—that is, no obvious telecommunications equipment. Students learn about how engineers design satellites to benefit life on Earth.
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Jeff White; Penny Axelrad; Malinda Schaefer Zarske; Janet YowellSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Satellite Division of the Institute of Navigation (www.ion.org) and National Science Foundation GK-12 grant no. 0338326.
Last modified: October 1, 2021






User Comments & Tips