Lesson Where Am I:
Navigation and Satellites

Learning Objectives

After this lesson, students should be able to:

• Explain how triangulation is used to find a location.
• Define global positioning system (GPS) and explain why it is useful.
• List several different ways engineers help locate people on Earth.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Introduction/Motivation

Spacewoman Tess is now in space. Having deployed her satellites, she is now happily exploring outer space. Daughter, Maya, has been paddling her canoe north into Canada for over a week now. Spaceman Rohan is excited and worried about both of them. Maya has carried a global positioning system unit with her so that she can determine where she is at all times and, in fact, call her father, Spaceman Rohan, on her satellite phone if she needs anything.

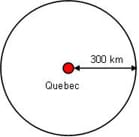
But, what exactly is a global positioning system (GPS) and how does it work? To better understand this, let's take a step back. GPS uses a concept called triangulation. What do you think triangulation might mean? It sounds like the word triangle. Well, it is kind of similar. Triangulation is finding a location of point by measuring the distance from two or more other known points.

Let's say that Maya does not have her GPS unit or her satellite phone and is totally lost in Canada. Maya has just met a talking beaver building a dam where she camped for the night. She asks him where he thought they might be. He replies, "I just walked and swam from Quebec and it took me 10 hours at 30 kilometers per hour." How far did the beaver travel? (Answer: 10 times 30 = 300 kilometers.) What does this tell Maya? Think about it like this (draw Figure 1 on the board): if Quebec is the center of a circle and Maya is 300 km from Quebec, then she could be anywhere on the circle (but not inside the circle). So now Maya has one piece of information, she is somewhere on the outside of this 300 km radius circle around Quebec.

Now what? It just so happens that Maya has also met a talking bird, a Blue Heron to be specific. She has asks the bird where they are, and the bird says that he has just flown from New Brunswick. It took 10 hours flying really fast at 50 km per hour. How far did she fly? (Answer: 10 times 50 = 500 kilometers) So now, what other piece of information does Maya know? She now knows that she is also 500 kilometers from New Brunswick. If the Blue Heron's information is combined with the beaver's information, we have two circles combined (draw Figure 2 on the board). If Maya is 300 km from Quebec AND 500 km from New Brunswick, then there are only two possible points that she can be. Can you point out these two points on the drawing?

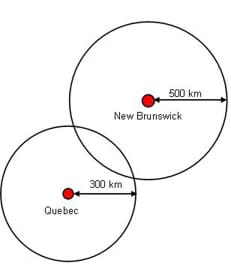
Okay, do we need one more piece of information? Yes! We need to know on which of those two points we are located. Well, Maya also met a talking fish who recently swam all the way down from Sept-Les. Wow! The talking fish told her that she swam 20 kilometers per hour and it took her 20 hours to get to where Maya was. How far did she swim? (Answer: 20 times 20 = 400 kilometers) So now Maya knows that she is also 400 kilometers from Sept-Les. If the fish's information is combined with the Blue Heron's and beaver's information, then we have three circles (draw Figure 3 on the board).

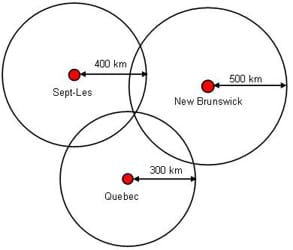
Maya now knows that she is 400 km from Sept-Les, 500 km from New Brunswick, and 300 km from Quebec. With this information, we know she can only be at one point. Where on the drawing must Maya be? (Answer: The only point where the three circles intersect—the only point that is on all three circles exactly the radius of each circle away from its center.)

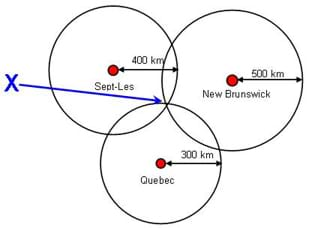
This geometrical concept is called triangulation and can be used on a larger and three-dimensional scale with satellites to pinpoint exactly where on Earth a person is. This short exercise that we just did gave Maya her position, which can be converted into a coordinate on the Earth using longitude and latitude.

But is the Earth a circle? What is the three-dimensional equivalent of a circle? (Note: If this question is not readily answered, ask students: What does a flat basketball look like? A circle. What does a full basketball look like? A sphere!) So with our two-dimensional drawing, we needed three circles to pinpoint our location. What are the three dimensions? Two of them are longitude and latitude. What is the other one? What about how far away from the Earth's surface we are? Might a mountain climber like to know how far she is from the summit? Possibly. The other dimension is altitude. Exact locations are determined by using longitudinal, latitudinal and altitudinal information from navigation satellites that orbit the Earth.

Usually, we will not run into talking beavers, talking Blue Herons and talking fish in the middle of nowhere, so if we need to know exactly where we are, we rely on other forms of technology. Global positioning satellites (GPS) work in remote areas. GPS uses a concept similar to triangulation, combined with orbiting satellites in space, to pinpoint specific Earth locations. Refer to the associated activity Find It! to help illustrate the concepts of this lesson.

Lesson Background and Concepts for Teachers

Global Positioning System (GPS)

Navigation satellites are like orbiting landmarks. Rather than seeing these landmarks with our eyes, we "hear" them using radio signals. A global positioning system is a constellation (or set) of at least 24 satellites that continuously transmit faint radio signals toward the Earth. These radio signals carry information about the satellite location and special codes that enable someone with a GPS receiver to measure distance to the satellite. Combining the distances and satellite locations, the receiver can find its latitude, longitude and height (altitude).

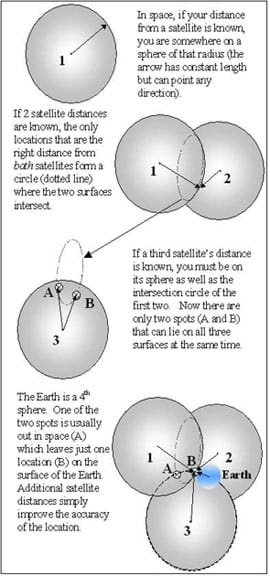
How does a GPS receiver know how far away the satellites are? Given velocity and the time required for a radio signal to be transmitted between two points, the distance between the two points can be computed; the transit time can be measured and is then multiplied by the exact speed of light to obtain the distance between the two positions.

GPS is based on satellite ranging. Our position on Earth is calculated by measuring our distance from a group of satellites in space. This is done by timing how long it takes a radio signal to reach us from a satellite. The signal travels at the speed of light (186,000 miles per second), enabling us to calculate the distance (velocity x time = distance).

GPS satellite ranging enables a receiver to determine its three-dimensional position: latitude, longitude and height. Because the ranging measurements are based on timing, the time in the satellite transmitter and the user's receiver must be coordinated. A GPS receiver measures range to four satellites to determine latitude, longitude, height and this timing correction.

Let's take this one step at a time. For now, assume that the satellite and receiver clocks are already coordinated and the positions of the satellites are known. If we measure distance to one satellite, we know that we are located on a sphere of that radius, centered on the satellite. With two satellite range measurements, our location is limited to a circle and with three satellites to one of two points. A fourth satellite can be used to find the correct point and to take care of the time coordination.

So, how do we know where the satellites are located? All satellites are constantly monitored. They have a 12-hour orbit and the U.S. Department of Defense is able to monitor the satellites from ground stations around the world. The satellites are checked for errors in their position, height and speed. These minor errors are caused by gravitational pulls from the moon, sun or even pressure from solar radiation on the satellite. The satellites transmit special codes for timing purposes, and these codes carry a data message about their exact location. These codes help to precisely locate the satellite.

Associated Activities

• Find It! - Students learn how triangulation and global positioning systems (GPS) work.

Lesson Closure

In this lesson, we learned that we can determine a person's location through the process of triangulation. What word does triangulation sound like? Yes, a triangle! And, how many sides does a triangle have? Three. So, how many points do we need to find a location? That's right: three (the point where you are located and two other points at a distance away). How many satellites do we need to find a person using GPS? Yes, also three. In two dimensions, and using the distances between specific places, a person's coordinates on the Earth (latitude and longitude) can be figured out by triangulating with two known points. In three dimensions, using navigation satellites and global positioning systems, a person's coordinates (latitude, longitude and altitude) can be determined using satellites and the data on their respective distances from Earth.

Vocabulary/Definitions

altitude: The elevation (height) of an object from a known level.

latitude: Imaginary lines that cross the surface of the Earth parallel to the Equator, measuring how far north or south of the Equator a place is located.

longitude: Imaginary lines that cross the surface of the Earth, running from north to south, measuring how far east or west of the prime meridian a place is located.

navigation: The science and technology of finding the position and directing the course of vessels and aircraft.

orbit: The path of a celestial body or an artificial satellite as it revolves around another body.

satellite: An object that travels around another object or any object in orbit about some body capable of exerting a gravitational force.

triangulation: A method of surveying so that the location of an object may be calculated from the known locations of two other objects.

Assessment

Pre-Lesson Assessment

Brainstorming: As a class, have students engage in open discussion. Remind them that in brainstorming, no idea or suggestion is "silly." All ideas should be respectfully heard. Take an uncritical position, encourage wild ideas and discourage criticism of ideas. Have students raise their hands to respond. Write their ideas on the board.

• Ask students to individually think about how they can know where they are, describe to other people where they are, or know where other people are. (Answers may include: ask people, use a compass, identify landmarks, read a map, etc.)

Question/Answer: With students working together in groups of two to three, have them answer the following questions. Discuss their answers as a class.

• Ben is on the outside of a circle and Shali is in the center of the circle. They are five meters away from each other. What is the radius of the circle? (Answer: Five meters.) What is the diameter of the circle? (Answer: 10 meters.)
• Ben is on the outside of a circle and Shali is in the center. Again, they are five meters away from each other. To walk to Shali, it takes Ben one hour. How fast can Ben walk? (Answer: Five meters every hour, so five meters per hour.) If Ben walks this fast all the time, how far can Ben walk in three hours? (Answer: Five multiplied by three, so 15 meters, or 5 X 3 = 15 meters.)
• Now the circle is much bigger, and Ben is lost in space very very far away from Earth, perhaps near Jupiter. He is sending a signal to Shali, who is still on Earth. The signal travels 300,000 kilometers per second and the signal takes two seconds to reach Shali. How far away is Ben? (Answer: 600,000 kilometers away from Earth.)

Post-Introduction Assessment

Where Am I? With students in groups of four, tell them that student 1 is lost. Her three friends (students 2, 3 and 4) know how far away from student 1 they are, though none of them can see each other. Their distances from each other are as follows:

• Student 2 is 5 meters from student 1.
• Student 3 is 10 meters from student 1.
• Student 4 is 2 meters from student 1.

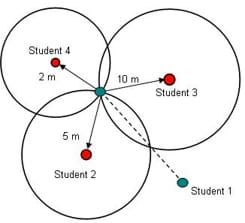
Ask the students to do three tasks:

1. Discuss with their teammates how they might solve the problem.
2. Sketch a drawing of the students in relation to one another.
3. Point out on the drawing where each student is.

Could this information also be used to find out how far student 2 is from student 3? How? What about student 2 from student 4? And student 4 from student 3?

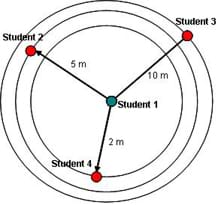
(An alternative solution to this problem is shown in Figure 7. Student 1 could be in the center of all of the circles. If none of the students come up with this solution, challenge them to find another solution. Finally, draw Figure 7 on the board.)

Post-Lesson Assessment

Navigation Engineers: In advance, hide an object in the classroom (somewhere on the floor) and measure its distance from each of the centers of three walls. Organize the class into six groups and tell students that you have hidden something on the floor of the classroom and they must work together to find the object. See Figure 8 for an illustration of the following group tasks.

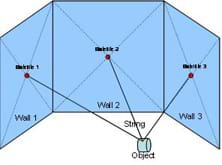
• Group 1: This group is Satellite 1 located on Wall 1, directly in the center of the wall. Group 1's job is to locate exactly where on the wall Satellite 1 is (that is, find the center of the wall). They tape a piece of paper to the wall representing their satellite.
• Group 2: This group is Satellite 2, located on Wall 2, directly in the center of the wall. Group 2's job is to locate exactly where on the wall Satellite 2 is (that is, find the center of the wall). They tape a piece of paper to the wall representing their satellite.
• Group 3: This group is Satellite 3, located on Wall 3, directly in the center of the wall. Group 3's job is to locate exactly where on the wall Satellite 3 is (that is, find the center of the wall). They tape a piece of paper to the wall representing their satellite.
• Group 4: This group is Satellite 1's distance from the object, which is XX meters (determine this measurement in advance). Group 4's job is to measure and cut a string this length.
• Group 5: This group is Satellite 2's distance from the object which is XX meters (determine this measurement in advance). Group 5's job is to measure and cut a string this length.
• Group 6: This group is Satellite 3's distance from the object which is XX meters (determine this measurement in advance). Group 6's job is to measure and cut a string this length

After students have found the hidden object, ask the class the following questions:

• Let's imagine that these are real satellites that are moving in a circular orbit. If they move, does the length of the string change? (Answer: No, since the orbit is circular, the satellite is always the same distance away from the center of the orbit.)
• If Satellite 3 malfunctioned, would we have still been able to locate the object? (Answer: Maybe; we know the object was on the floor, so we could have searched the entire floor. Although it would have taken a while, it would be possible. But, if the floor and our classroom were super large, it would have been very difficult to find the object without all three of the satellites.)

Triangulation Math Extension: Have students work in pairs to come up with their own 2-D or 3-D triangulation problem. They can choose an object and measure the distance to it from three points. Have them write down which three points they used and the distances from those points to the mystery object. Then have pairs exchange their problems with another pair of students to solve.

Point 1: ______________ Distance to object: __________

Point 2: ______________ Distance to object: __________

Point 3: ______________ Distance to object: __________

The object I am looking for is: ______________________

Lesson Extension Activities

For upper grades, have student groups hide objects in the classroom and make up lists of data (measurements to the center of the walls) for other groups to find the objects.

Have students come up with two different ways of describing how to find a location and then have them use their descriptions to find the location. Next, have students discuss which parts of the descriptions worked better or worse.

Using the skills they learned in this unit, have students create a poster of the story of Spacewoman Tess, Spaceman Rohan and their daughter, Tess. Have them explain one engineering concept they learned. They can tell the story of Tess getting into space or Maya communicating with her parents.

References

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under grants from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation (GK-12 grant no. 0338326). However, these contents do not necessarily represent the policies of the DOE or NSF, and you should not assume endorsement by the federal government.