Quick Look
Grade Level: 4 (3-5)
Time Required: 45 minutes
Expendable Cost/Group: US $1.00
Group Size: 3
Activity Dependency: None
Subject Areas: Earth and Space, Physical Science, Science and Technology

Summary
Students learn the basic concept of global positioning systems (GPS) using triangulation and measurement on a small scale—within boxes in the classroom. They discover how GPS and navigation integrate mathematics and scientific concepts to create a standard for locating people and objects. This activity helps students understand both the need for and methods of navigation.Engineering Connection
Engineers are involved in the design of satellites, getting them into space, and analyzing the data retrieved from them. GPS designed by engineers helps to determine precise locations of receivers on Earth. GPS has become a common technology in vehicle and phone designs. Engineers work with the communication systems, from satellites to information highways, which help people contact each other from great distances.
Learning Objectives
After this activity, students should be able to:
- Describe a satellite and how it helps in locating a person on Earth.
- Explain how triangulation is used to find a location.
- Describe how engineers are involved in the design and use of satellites.
- Use strings to measure distances between points.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
International Technology and Engineering Educators Association - Technology
-
Judge technologies to determine the best one to use to complete a given task or meet a need.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Represent and interpret data.
(Grade
3)
More Details
Do you agree with this alignment?
-
Appropriate measurement tools, units, and systems are used to measure different attributes of objects and time.
(Grade
4)
More Details
Do you agree with this alignment?
Colorado - Science
-
Develop a scientific explanation regarding relationships of the components of the solar system
(Grade
4)
More Details
Do you agree with this alignment?
Materials List
Each group needs
- 1 medium-sized box, ~15 L x 11 W x 7-inches H (38 x 28 x 18 cm); best if the box height is less than its width and length
- 5 feet (1.5 m) of string
- scissors
- ruler
- tape
- Bottom of Box Map, one per group
- Measurement Data Recording Sheet, one per person
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_rockets_lesson06_activity1] to print or download.Pre-Req Knowledge
The ability to accurate measure length using a ruler.
Introduction/Motivation
How is it possible that we can ever pinpoint exact locations on the Earth when it is so huge? How about finding an exact location in space? Do you think that is hard? Yes, it is! Often, we create small-scale models to represent large-scale objects, like a globe of the Earth. This helps us gain a better understanding of where things are in relation to each other. The small-scale model is usually a good representation of the real thing. Can you point out the USA on the globe? How about Africa? Now, let's think of Maya canoeing around Canada. Where might she be? Sure, we can point at the area where Maya might be, but how do we find out exactly where she is? Well, today we will learn how engineers help us find our location anywhere on Earth using a technology called global positioning system (GPS) and satellites in space.
Satellites can help us know exactly where something is on Earth. Have you ever looked outside at night and seen a star that is moving slowly though the sky? Well, that may not be a star and might be a satellite instead. Hundreds of satellites are orbiting the Earth as we speak. In fact, the Earth even has a natural satellite. Do you know what it is? The moon! Engineered or human-made, satellites can be instruments or machines that record different data measurements from outside the Earth's atmosphere for various purposes such as scientific research, weather research and prediction, navigation and observing the Earth. GPS satellites help us find a location by triangulating the position of an object or person as they move. Satellites do this by receiving and transmitting signals. Basically, a signal is sent from a computer or a person in one location on Earth up to a satellite orbiting the Earth and back down to the same or another person or computer somewhere else. (Refer to Lesson 1 of this unit for additional discussion about satellites and communication.)
With Spacewoman Tess in space (having deployed her satellites), Spaceman Rohan on the ground hoping to get in contact with Maya, and Maya off paddling in her canoe with her satellite phone and GPS receiver, the entire family needs to be able to be in contact with each other. But, in order to communicate with each other, this family needed to understand the science and math behind communications in order to set up their system. Tess had to learn about satellites to design one and get it into space, and Rohan and Maya needed to learn about how communications work on Earth.
Engineers invented satellites and have always been involved with designing them, getting them into space, and analyzing their data. So, engineers need to have a good understanding of science, space and aerospace engineering. Engineers also need to understand mathematics and navigation systems on Earth. Today, we are going to act as if we are engineers and use math to find a location of someone on a map. We will pretend that the map is a city and we will figure out how many satellites we need to find our exact location. We can find that location by modeling GPS satellites and receivers.
Procedure
Teacher Background
The activity consists of two parts. First, students in groups of two or three each receive a box, map, ruler and scissors. Each team picks a place on the map where they want their "unknown" location to be; perhaps this location represenst where they are, where a little bug is, or even where in Canada Maya is located. Then they measure the distance from that location on the map to the center of three of the sides of the box. Now, their box has a location on it, and three measurements to go along with it.
Second, the groups trade boxes. With the information given with the boxes, students use the measurements to cut the string into each of the three lengths, measure from the center of each of the sides, and find the location of the object. Then they check with the students who made the model to see if they are correct.
Before the Activity
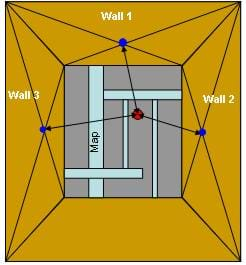
- Obtain enough boxes (one per team) and cut off the four top flaps (the flaps that would be used to "close" the box) to make it easier for students to conduct the activity.
- User a marker to mark the center points on the three inner walls/sides of each box. Do this by drawing lines to opposite corners on each box side, and finding the intersections, which are the center points (see the blue dots on Figure 1).
- Label the walls as shown on Figure 1: wall 1, wall 2, wall 3.
- Make copies of the Bottom of Box Map, one per team. Then glue or tape a map to the inside bottom of each box as shown in Figure 1.
- Make copies of the Measurement Data Recording Sheet, one per student.
- Cut the string into 5-foot lengths.
With the Students
- Divide the class into groups of two or three students each, depending on the class size and number of boxes. Tell them that today they are acting as if they are engineers who using triangulation to find an exact location. Write the word "triangulation" on the board. Go over the procedure with the students.
- Have groups each choose a mystery location on the map in the bottom of the box---but DO NOT place a location marker on the map because it will be the challenge for another group to try and find that location with the data given them. Direct the teams to write the mystery location in the space provided on data sheet.
- After each group has chosen a specific location on the map, have students measure the distance from that point to each of the center marks on each of the three marked ininer walls of the box using string and a ruler. Students should not cut the string. They should record these values on the data sheet.
- Next, have groups trade their boxes and data sheet with another group. The challenge is to see if the other group can accurately locate the first group's mystery location given the data the group recorded on the data sheet.
- Now with a new box from the another group, have students measure and cut their string into three pieces according to the recorded length on the other group's data sheet. Then the group as three strings that go from the center of each of three walls of the box to the map.
- Using the three cut strings from the side walls, direct students to find (triangulate) the mystery location on the map. To do this, have them tape each length of string to the matching center of the wall, pulling all of the strings tight and see where they meet on the map. Once they think they have the location, have them make a mark on the map.
- Have groups retrieve their original boxes and verify if the other group found the correct mystery location.
Assessment
Pre-Activity Assessment
Brainstorming: In small groups, have students engage in open discussion. Remind them that no idea or suggestion is "silly." All ideas should be respectfully heard. Ask the students:
- What are different ways that distance is used to measure and communicate where things are. (Example answers: My house is 2 km from school, or giving directions, such as: Go three blocks and then turn right, etc.)
Activity Embedded Assessment
Worksheet: Have students record measurements and follow along with the activity using the Measurement Data Recording Sheet. After students have finished the data sheet, have them trade mystery locations with their peers.
Group Questions: During the activity, ask the groups:
- Can you think of other ways that you could describe the location of a specific point using distances. (Answer: Measure from landmarks, measure from different points, include height measurements, etc.)
- What might happen if accurate measurements are not give to the other group? (Answer: The other group will have a hard time finding the location.)
- If this was not on a small scale and the point is the real location where someone was lost, what would happen if an engineer did not accurately report the measurements? (Answer: That person might stay lost for a longer time.)
- What we are doing is called triangulation. Can you think of why? What word does triangulation remind you of? (Answer: A triangle. A triangle has three corners. We are using three strings to find our point and basically making a pyramid or three-dimensional triangle on the map.)
Post-Activity Assessment
Question/Answer: Ask the students and discuss as a class:
- This was a small-scale model of what a GPS system does. In a real GPS system, the points on walls of the box represent what? (Answer: Navigation satellites.)
- If you wanted to specify a point some distance above the bottom of the box, what additional information would you need to provide? (Answer: The distance between the bottom of the box and that point or height.) In a large-scale system, like the Earth, what would that distance represent? (Answer: Altitude.)
- What geometrical concept did we use to find the specified location? (Answer: Triangulation.)
- Is this the same method that GPS satellites and receivers use to find a specified location? (Answer: Yes.)
- How many satellites did we need to find our location on Earth? (Answer: Three.)
- How would you define triangulation? (Example answer: Triangulation is finding a location of point by measuring the distance from two or more other known points; finding a location on a map, in three dimensions, which takes at least three satellites to find the exact location; making a three-dimensional triangle or a pyramid.)
- What do engineers need to understand to design satellites for GPS? (Answer: Engineers need to have a good understanding of science, space and aerospace engineering.)
Writing Procedures: Have students write out steps for how to find the mystery location. How does this model relate to real life?
Troubleshooting Tips
- If the measurements are not carefully made and recorded, the other groups will have a very hard time finding the correct mystery location. So remind students to be precise.
- If the initial group does not record or remember where their specific location is, it is difficult to reconcile the answers. So ask groups to write the location in the space provided on the data sheet.
Activity Extensions
- Have students write a story about the map and the specified location.
- Make a map of the room, the state, the country or the world, and specify points on the map and triangulate their positions.
Activity Scaling
- For upper grades, have students find the center of the walls of the box themselves and do not label the box walls for them.
- For upper grades, have students specify two locations on the map and then have the other group find both points and the distance between those two locations.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students explore the concept of triangulation that is used in navigation satellites and global positioning systems designed by engineers. Also, students learn how these technologies can help people determine their positions or the location of someone else.

In this lesson, students explore the role of communications and how satellites help people communicate with others far away and in remote areas with nothing around—that is, no obvious telecommunications equipment. Students learn about how engineers design satellites to benefit life on Earth.

Students explore using a GPS device and basic GIS skills. They gain an understanding of the concepts of latitude and longitude, the geocaching phenomenon, and how location and direction features work while sending and receiving data to a GIS such as Google Earth.

During a scavenger hunt and an art project, students learn how to use a handheld GPS receiver for personal navigation.
Copyright
© 2006 by Regents of the University of ColoradoContributors
Jay Shah; Malinda Schaefer Zarske; Janet YowellSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under grants from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education, and National Science Foundation (GK-12 grant no 0338326). However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: August 10, 2017









User Comments & Tips