Quick Look
Grade Level: 8 (6-8)
Time Required: 45 minutes
Lesson Dependency: None
Subject Areas: Earth and Space, Science and Technology
NGSS Performance Expectations:

| MS-PS2-2 |

Summary
The purpose of this lesson is to teach students how a spacecraft gets from the surface of the Earth to Mars. Students first investigate rockets and how they are able to get us into space. Finally, the nature of an orbit is discussed as well as how orbits enable us to get from planet to planet — specifically from Earth to Mars.Engineering Connection
Aerospace engineers play an important role in the design of rockets for space exploration. These engineers must have a thorough understanding of Newton's third law of motion — or else the rockets would not leave the Earth's surface! Engineers are also experts in the concepts of thrust and specific impulse, so they are able to design efficient rockets. Engineers also lead the research that has resulted in the three primary rocket types used in space applications: chemical rockets, electrical rockets and cold gas rockets.
Learning Objectives
After this lesson, students should be able to:
- Describe how a rocket must overcome the forces of gravity and drag in order to get out of the atmosphere.
- Explain that thrust is the force created by a rocket.
- Describe how an orbit is the balance of gravity and an object's tendency to follow a straight path.
- Explain some challenges that engineers face in getting a rocket to Mars.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-PS2-2. Plan an investigation to provide evidence that the change in an object's motion depends on the sum of the forces on the object and the mass of the object. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Plan an investigation individually and collaboratively, and in the design: identify independent and dependent variables and controls, what tools are needed to do the gathering, how measurements will be recorded, and how many data are needed to support a claim. Alignment agreement: Science knowledge is based upon logical and conceptual connections between evidence and explanations.Alignment agreement: | The motion of an object is determined by the sum of the forces acting on it; if the total force on the object is not zero, its motion will change. The greater the mass of the object, the greater the force needed to achieve the same change in motion. For any given object, a larger force causes a larger change in motion. Alignment agreement: All positions of objects and the directions of forces and motions must be described in an arbitrarily chosen reference frame and arbitrarily chosen units of size. In order to share information with other people, these choices must also be shared.Alignment agreement: | Energy may take different forms (e.g. energy in fields, thermal energy, energy of motion). Alignment agreement: |
Common Core State Standards - Math
-
Fluently divide multi-digit numbers using the standard algorithm.
(Grade
6)
More Details
Do you agree with this alignment?
-
Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
(Grade
6)
More Details
Do you agree with this alignment?
-
Use variables to represent quantities in a real-world or mathematical problem, and construct simple equations and inequalities to solve problems by reasoning about the quantities.
(Grade
7)
More Details
Do you agree with this alignment?
-
Use numbers expressed in the form of a single digit times an integer power of 10 to estimate very large or very small quantities, and to express how many times as much one is than the other.
(Grade
8)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Transportation vehicles are made up of subsystems, such as structural propulsion, suspension, guidance, control, and support, that must function together for a system to work effectively.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Reason quantitatively and use units to solve problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Describe methods and equipment used to explore the solar system and beyond
(Grade
8)
More Details
Do you agree with this alignment?
-
Recognize that mathematical models are used to predict orbital paths and events
(Grade
8)
More Details
Do you agree with this alignment?
Introduction/Motivation
How does a rocket physically get from the Earth to Mars? (Expect students to indicate that it takes a very large rocket to get there.) Why do you need such a large rocket? (Expect answers such as: We need to overcome gravity, Mars is a far away, when we go to Mars, we have to take a lot of supplies and equipment, and maybe even, we have to overcome gravity and the drag of our atmosphere.)
So, as soon as we leave the atmosphere, are we free to travel to Mars? Not quite yet, we are still in the grip of Earth's gravity even though the astronauts feel weightless. There is a misconception that once you leave the Earth's atmosphere, there is no gravity. The truth is that there is gravity acting on a person in orbit around the Earth - but they do not feel it. A comparison can be made to a sky diver. Do you think a sky diver feels the effects of gravity? The answer is no, a sky diver cannot feel gravity. S/he can feel the air rushing by and see the ground coming up but s/he cannot actually feel gravity. This feeling is called weightlessness, and it does not mean that gravity is not there. It is as if both the astronaut and spacecraft are perpetually falling, but never actually get any closer to the surface of the Earth.
So, once a rocket has taken us out of the Earth's atmosphere, we enter into an orbit around the Earth. What is an orbit? (Listen to student suggestions). An orbit is a regular, repeating path that one object in space takes around another one. What is the shape of most orbits? (Listen to their answers; most will suggest the shape of a circle.) It is elliptical. An ellipse is essentially an oval. While a circle is a special kind of ellipse, engineers and scientists use the term ellipse to describe orbits around Earth and other bodies such as the Sun. So, if a spacecraft is in orbit around Earth, how does it get to Mars? (Listen to student answers.) Well, it uses another rocket. If the rocket moves the craft fast enough, it can overcome the Earth's gravity and start heading for Mars. Students can illustrate this idea with the hands-on activity, The Great Gravity Escape. Elliptical orbits also help to move a rocket between planets. However, many other factors must be taken into consideration when traveling between planets. Today we are going to talk about the basics of traveling from Earth to Mars.
Lesson Background and Concepts for Teachers
Getting off Earth – Launch
The first step on the trip to Mars is the launch. Launch is the act of getting a spacecraft off the surface of the Earth and into an orbit around it. It takes a lot of energy to reach an orbit above Earth. Consider that just to jump a couple feet off the ground takes all the energy we can muster. To get a thousand kilogram spacecraft off the ground takes an incredible amount of energy. Not only do we have to overcome Earth's gravity, but also the drag of the atmosphere.
Let's consider the forces acting on a rocket. Look at Figure 1 showing a rocket just before liftoff. The two forces acting upon the rocket in this scenario are the rocket's weight (W) and a normal force (N). A normal force is a force that acts on an object by a contact surface (in this case, the ground). A normal force also acts perpendicularly to the surface – because the ground is horizontal, the normal force acts vertically. If we add the forces together, we will find the net force (Fnet) acting on the rocket: Fnet = N – W. The weight is preceded by a minus sign because the weight of the rocket acts downward (the normal force acts upward and is thus positive, but does not require a plus sign by common mathematical sign convention). It is easy to understand from this situation that because the rocket is not moving, the weight is balanced by the normal force: N = W. Thus, the net force is zero.
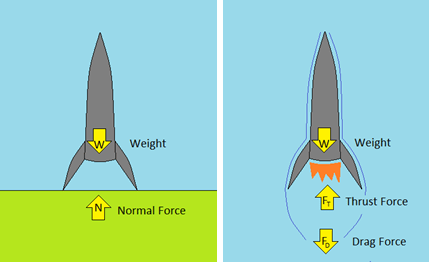
Now let's consider the scenario after liftoff. Look at Figure 2. There is no longer a normal force because the rocket is not in contact in the ground. The positive (up) force is now the thrust force (FT; more on this later). Because the rocket is travelling in Earth's atmosphere, there is a drag force (FD; we can feel drag when we put our hands out a moving car's window). Let's find the net force acting on this rocket: Fnet = FT – FD – W. The motion of the rocket depends on the magnitudes of these forces at an instant in time.
If the thrust force is less than the sum of the drag force and the weight (i.e., the downward forces are greater than the upward force), then the rocket will fall back to the Earth.
If the thrust force is equal to the sum of the drag force and the weight, then the rocket will continue travelling upward at the same velocity (it will not speed up or slow down). This scenario describes Newton's 1st Law of Motion – this law (known as the "law of inertia") simply means that if an object is in motion and is not acted upon by unbalanced forces, the object will remain in motion at the same velocity (it will not accelerate or decelerate). (The 1st Law also describes the scenario in Figure 1 – if an object is at rest and is not acted on by unbalanced forces, it will remain at rest.) In order to be travelling fast enough to orbit, the rocket must reach a minimum velocity of 8 kilometers per second (discussed later). If it does not reach this velocity, it will eventually fall back to Earth.
If the thrust force is greater than the sum of the drag force and the weight, then the rocket will accelerate upward (the velocity will continue to increase). This scenario illustrates Newton's 2nd Law of Motion. The 2nd Law can be described mathematically by the equation Fnet = ma, where m is the mass of the rocket and a is its acceleration. Thus, it is easy to see that the acceleration of a rocket is dependent upon the net force and the mass of the rocket.
If we rearrange the equation for Newton's 2nd Law of Motion so that a is by itself (divide both sides by m), then we have:
Now we can more easily see the effect of the rocket's mass on its acceleration. When the mass increases, the acceleration decreases. When the mass decreases, the acceleration increases. We can describe this mathematically as shown below:
This demonstrates the importance of keeping the mass of a rocket to a minimum – doing so will allow the rocket to accelerate much faster.
To figure out how much velocity we need to get into an orbit around Earth, we use the following equation:
where, ∆ means change and V means velocity.
So ∆VLaunch is the total change in velocity needed to launch a spacecraft into an orbit around Earth. ∆V is the final velocity minus the initial velocity. Since the velocity of the spacecraft is initially zero while it is on the ground, ∆V is simply the final velocity. ∆Vburnout is the leftover velocity that we need to maintain and orbit around Earth. We will talk about this velocity a little later. ∆Vgravity is the change in velocity needed to overcome the gravity of Earth. ∆Vdrag is the change in velocity required to overcome drag.
To achieve the required ∆V, engineers at NASA use huge rockets. The actual size and mass of the rocket, which engineers call the launch vehicle, dwarfs the actual spacecraft, which is referred to as the payload. For a typical mission into Low Earth Orbit (LEO) the mass of the launch vehicle and the fuel is roughly 40 times the mass of the actual payload.
So, how does a rocket create the ∆V we need? (Answer: Rockets take advantage of what is described in Newton's third law of motion.) Newton's third law states that for every action there is an equal and opposite reaction. If you were to stand on a skateboard and push against a wall you would move in the opposite direction. This is an example of Newton's third law. Cars use tires to push backwards against the road, which causes them to move in the opposite direction. True, rockets do not actually push against the air, but the movement of a rocket is still described by Newton's third law of motion. A rocket works by creating super hot gasses and "throwing" them backwards very quickly. This "throwing" of the air is the action. The reaction is that the rocket moves in the opposite direction, forwards.
We use two basic numbers to characterize rockets. The first of is the thrust — the force that pushes the rocket into orbit. We calculate the amount of thrust a rocket produces by using the following equation:
where the thrust force (F) is equal to the mass flow rate (m) multiplied by the exhaust velocity (Ve). The mass flow rate is how fast mass is coming out of the rocket. The mass is the exhaust gas that comes from the burning fuel. Mass flow rate is measured in kilograms per second (kg/s). The exhaust velocity is a measure of how fast the hot gas leaves the rocket nozzle.
The other number we use to characterize rockets is the specific impulse (Isp) — a measure of the energy content of a propellant and how efficiently it is converted into thrust. Basically, the specific impulse tells us how much "bang for the buck" we get out a certain type of rocket. To calculate the specific impulse, we divide the thrust by the weight flow rate:
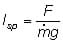
The weight flow rate is the mass flow rate (m) multiplied by the gravitational acceleration of Earth (g = 9.81 m/s2). The specific impulse has units of seconds. The Isp measures how much thrust we are getting for how much fuel weight we are using. A higher Isp means that we are getting more thrust for less fuel, and it is a more efficient system.
Three different kinds of rockets are currently used in space applications: chemical, electrical and cold gas. Chemical rockets are the most common type in use today, and include liquid fuel rockets, solid fuel rockets and a hybrid of the two. Chemical rockets rely on chemical combustion that creates a super-heated, high-pressure gas. This high-pressure gas can only escape through the nozzle. According to Newton's third law of motion, this gas leaving the rocket at a very high velocity is the action, while the rocket moving in the opposite direction is the opposite reaction.
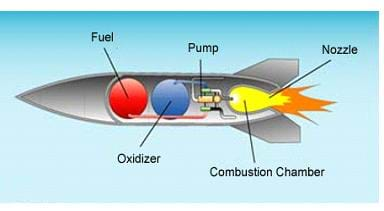
Liquid fuels are stored in large tanks and are pumped into a combustion chamber where they ignite before leaving the rocket through the nozzle. Figure 1 shows a diagram of a liquid fuel rocket. Liquid fuel systems are complicated since they require several tanks, complex valves and intricate piping, but they create a lot of thrust, have a high Isp, and can be throttled and restarted if needed. The space shuttles main engines use a liquid fuel that is a mixture of liquid oxygen and liquid hydrogen. Figure 2 shows the liquid fuel tank and the liquid fuel main engine on the space shuttle.

Solid fuel rockets can be described as a tube, filled with a solid fuel, capped at one end and with a nozzle at the other end. The solid fuel is highly flammable and works in the same way the liquid fuel system works. As the fuel burns, a hot and high-pressure gas comes out of the nozzle creating thrust. Solid fuel systems are very simple, cheap and reliable, but they cannot be turned off once they start and they are not as efficient as liquid fuels. An example of a solid fuel system is the Solid Rocket Boosters (SRB) on the space shuttle (see Figure 2). They are the two white rockets strapped to the side of the vehicle and are used to help get the space shuttle off the ground. Once the fuel inside the boosters is exhausted, they are released from the shuttle and dropped into the ocean. Bottle rockets and model rockets are both considered solid fuel rockets.
Electrical rockets use electricity to accelerate particles that are directed out the back end of the spacecraft, thus creating thrust. The rockets generally use charged atoms called ions that have a positive or negative charge associated with them. An electrical source, such as solar cells, or a nuclear reactor is used to charge plates in the engine with different charges so that the ions are pushed and pulled out of the spacecraft. The downside to electrical rockets is that they cannot create much thrust. If you hold one sheet of paper in your hand, the force with which the paper pushes on your hand due to its weight is roughly equal to the thrust of an electrical rocket. The plus side to electric rockets is that they are very efficient and have a high Isp. Since the thrust of an electrical rocket is so small, it is impossible to launch a rocket into space; but, once a spacecraft is in an orbit around Earth, an electrical rocket can be used to escape the Earth's gravity and head to different places around our solar system. The small thrust means it takes a long time for the craft to build up sufficient escape velocity, but the high efficiency of the system means less fuel is needed to achieve the desired velocity. The first use of electrical rockets in space was onboard Deep Space 1, which launched onboard a conventional liquid fuel rocket on October 24, 1998. Once it was in orbit, it started its own engine and eventually reached the Comet Borrelly in September of 2001.
Cold gas rockets use pressurized gas that is not ignited. This is usually a nonflammable gas such as nitrogen or helium. A balloon that is filled and then released is an example of a cold gas system. The pressurized gas can only escape out the nozzle, and as it does, it creates thrust. Cold gas systems have very low thrusts and are very inefficient (low Isp), but they are very simple and cheap. They are often used on spacecraft to make very small velocity changes where large rockets are overkill. The rocket packs that astronauts use when they are outside the space shuttle or international space station use cold gas rockets.
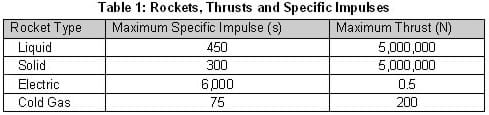
Table 1 shows the different types of rockets and the typical thrusts and specific impulses for each system.
Orbits
Once a launch vehicle has taken the spacecraft out of the Earth's atmosphere, it now must enter into an orbit. An orbit is a circular or elliptical path around a celestial body (sun, star, planet, asteroid, etc.) on which an object such as a spacecraft follows. One common misconception is that no gravity exists on the space shuttle and international space station. In fact, gravity is acting on a person in orbit around the Earth, but s/he does not feel it like we feel it on Earth, because no ground exists to push back on a person in space. So, why doesn't a spacecraft just fall back to Earth once the rockets shut off? This is because the velocity of the spacecraft wants to move it past the Earth, while gravity pulls it back. These two actions cancel out to form an orbit. An orbit can be explained by Newton's first law of motion, which tells us that an object in motion stays in motion unless a force acts against it. This means that an object will move in a straight line unless a force pushes it in a different direction. For any object to change the direction in which it is moving, a force must act upon it. For example, when you are on a bike and want to turn (change directions), your tire must apply a force to the ground. This force is called friction; without friction, it would be like biking on perfectly smooth ice. If you tried to turn, there would be no frictional force; you would keep moving in a straight line as Newton's first law describes. Just like your bike, a spacecraft will not turn unless a force acts on it. The force that acts on objects — ultimately causing them to orbit a planet or a star — is gravity. An orbit is just a balance between the velocity of an object and gravity.
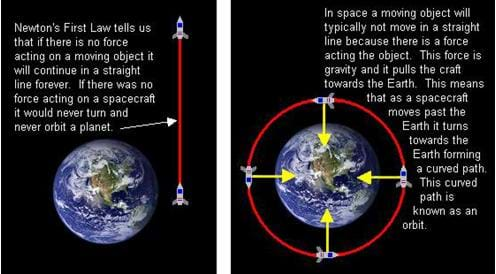
Figure 3 shows how gravity affects the path of a spacecraft. The diagram on the left shows the path of a spacecraft if there was no gravity. In this case, the spacecraft would continue along in a straight line. The diagram on the right shows the path of a spacecraft under the influence of gravity. Gravity is pulling the spacecraft towards the center of the Earth, while the velocity of the spacecraft makes the spacecraft want to keep going past the Earth. The balance of these two opposing actions is known as an orbit. For a low Earth orbit (LEO), which has an altitude between 600 and 2000 kilometers above the Earth's surface, the spacecraft must have a velocity of about 8 kilometers per second. That means that it can go all the way around the Earth in 90 minutes. So, what happens if the spacecraft is not moving (that is, it has no velocity)? If there is no velocity, then the only force acting on the spacecraft is gravity. This means that a spacecraft would fall to Earth just as a stone falls to the ground when you drop it. So, what happens if the spacecraft is moving much faster than the 8 km/s needed to maintain a LEO? In that case, the gravity will not be able to hold the spacecraft as close to the Earth, and the spacecraft will either move into an orbit that is further away from the Earth, or if it is moving fast enough it will overcome the Earth's gravity entirely. This is called the escape velocity, and it is the minimum velocity needed to escape the Earth's gravity.
Sir Isaac Newton performed a famous mind experiment to demonstrate how an orbit works that involves shooting cannons off the top of a mountain. See a demonstration of the cannon ball orbit on the NASA website at https://spaceplace.nasa.gov/how-orbits-work/en/.
Getting to Mars
Now that our spacecraft has left Earth's gravity, our mission is to arrive at Mars. We have left the influence of Earth's gravity, but we are not free of gravity altogether. Since we are now orbiting around the Sun, we are now under the influence of the Sun's gravity.
Thus far, we have talked about circular orbits — the simplest kind of orbit. However, most orbits are actually ellipses, a stretched circle. Ellipses are often called ovals. Figure 4 shows a diagram of an elliptical orbit.
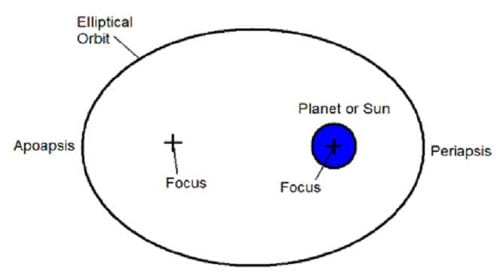
Two foci (each one called a focus) define an ellipse: the periapsis, which is the point on the elliptical orbit that is closest to the planet or sun; and the apoapis, the point furthest from the planet or sun. You may have also heard these points called perigee and apogee. These are the periapsis and apoapsis for an elliptical orbit around Earth, respectively. In an elliptical orbit, the Earth (or other massive body) is located at one of the two foci. Elliptical orbits enable movement between planets. Using the Sun as one of the foci, and the Earth as the periapsis, the spacecraft will actually be closer to the Sun when it is at the periapsis. When the spacecraft is at the apoapsis, it will be further away from the sun. This is useful for traveling to planets further from the Sun such as Mars. Figure 5 shows how half an elliptical orbit can be used to get from Earth to Mars.
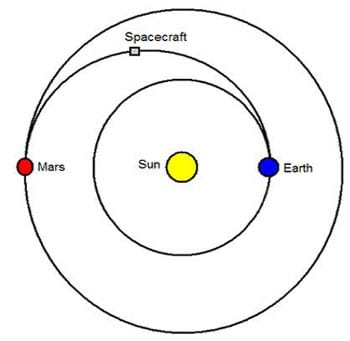
In addition to great engineering and excellent calculations by scientists, it takes good timing to reach Mars. Since the Earth and Mars are both moving, it is like standing on a moving platform and trying to shoot a basketball into a hoop that is moving as well. To make things worse, since it takes about 6 months for a spacecraft to go from the Earth to Mars, scientists and engineers have to anticipate where Mars is going to be when the spacecraft gets there. If we try to shoot a spacecraft right at Mars, by the time it actually gets there, the great Red Planet will be long gone. Once we get to Mars, we must slow down so that we are in an orbit around our destination. From our orbit, we can take photographs of Mars, take scientific readings, or even land on the planet.
Associated Activities
- The Great Gravity Escape - Students use water balloons and a length of string to understand how gravity and the speed of an orbiting body balance to form an orbit. They also see that when the velocity exceeds the escape velocity, the object will escape the gravity of the sun or planet that it is orbiting around.
Lesson Closure
In this lesson, the students should learn what it takes to get a spacecraft from the launch pad to Mars. We learned that rockets use the behavior described in Newton's third law of motion to propel upward/forward. We covered the basics of orbits and learned that an orbit is where the velocity of the spacecraft and the gravity balance to form an elliptical path. Finally, we talked about elliptical orbits and how elliptical orbits can be used to help us to travel from Earth to Mars.
Vocabulary/Definitions
apoapsis: The point in an orbit farthest from the center of attraction (that is, the planet or sun).
chemical rocket: A rocket that relies on a chemical combustion to create a super-heated, high-pressure gas that is used for thrust.
cold gas rocket: A rocket that uses escaping pressurized gas as a source of thrust.
electrical rocket: A rocket that creates thrust by using electricity to accelerate charged particles, which are directed out the back of the vehicle.
ellipse: A closed curve resembling a flattened circle. Most orbits are in the shape of an ellipse.
escape velocity: The minimum velocity needed to escape from the gravitational pull of a celestial body (Earth, Sun, etc).
foci: Two points on an ellipse in which the sum of the distances to the foci from any point on the ellipse is a constant.
Newton's 1st Law of Motion: For an object being acted on by balanced forces: if the object is at rest, it will remain at rest; if an object is in motion, it will remain in motion ("law of inertia").
Newton's 2nd Law of Motion: For an object being acted on by unbalanced forces: the acceleration of an object is dependent on its mass and the net force. Described by the equation Fnet = ma.
Newton's 3rd Law of Motion: For every action, there is an equal and opposite reaction.
normal force: A force provided by a contact surface (e.g., the ground) that acts perpendicularly to the surface.
orbit: The path of a planet, moon, spacecraft, or any other object in space as it revolves around another object, such as the sun.
periapsis: That point in an orbit closest to the center of attraction (that is, the planet or sun).
specific impulse: A measure of rocket efficiency that is equal to the thrust of the rocket per weight of the fuel.
thrust: The forward reaction to the rearward movement of exhaust from a rocket engine.
universal gravitational constant: The constant that relates the gravity of two objects depending on their masses and the distance between them.
Assessment
Pre-Lesson Assessment
Discussion Questions: Solicit, integrate and summarize student responses.
- What does it take for us to get to Mars? What does it take to get a spacecraft off the ground?
- What do you know about rockets? How do they work? Can you name any rockets? (Answer: US space shuttles: Saturn, Atlas, Titan, Delta, Ariane, Pegasus, etc.)
- Once a spacecraft is out of the Earth's atmosphere, it goes into an orbit. What is an orbit? (Answer: An orbit is a curved path on which a planet, star, spacecraft, etc. moves around another object or celestial body.)
Voting: Ask a true/false question and have students vote by holding thumbs up for true and thumbs down for false. Count the votes and write the totals on the board. Give the right answer.
- Is gravity acting on the space shuttle and its crew? (Answer: Gravity is acting on them and creates the centripetal force that keeps the space shuttle from flying in a straight line off into space. They do not feel it because the inertia of their orbit is perfectly balanced with the centripetal force from gravity.)
Post-Introduction Assessment
Discussion Question: Ask the students and discuss as a class:
- Why does it take so much energy to get to Mars? (Possible answers: We have to overcome the gravity of Earth; we have to overcome the drag of Earth's atmosphere; we have to get enough speed to get to Mars in a reasonable time; and/or we have to slow down once we get to Mars so we do not just fly past the planet.)
- If a rocket is moving at constant velocity and the thrust force is equal to the sum of its drag force and its weight, what will happen to the rocket? What law describes this situation? (Answers: The rocket will continue to move at the same velocity. Newton's 1st Law of Motion.)
- If a rocket constant is moving at constant velocity and the thrust force is less than the sum of its drag force and its weight, what will happen to the rocket? What law describes this situation? (Answers: The rocket will begin to fall back to Earth. Newton's 2nd Law of Motion.)
Lesson Summary Assessment
Numbered Heads: Divide the class into teams of three to five students each. Have students on each team pick numbers so each has a different number. Ask the students a question and give them a short time frame for solving it (~1 minute). The members of each team should work together on the question until everyone on the team knows the answer. Call a number at random. Students with that number should raise their hands to answer the question. If not all the students with that number raise their hands, give the teams more time to work on the question. Example questions:
- Which of Newton's laws of motion states that for every action there is an equal and opposite reaction? (Answer: Newton's third law of motion.)
- What must a rocket overcome in order to reach orbit? (Answer: Gravity and drag.)
- What is the force created by a rocket called? (Answer: Thrust.)
- What do we call the measurement of a rocket's efficiency? (Answer: Specific impulse.)
- What happens if a spacecraft in orbit slows down too much? (Answer: If the spacecraft slows down a little it moves into a lower orbit — closer to Earth; if the craft slows down too much it will not be able to maintain an orbit and will crash — if they did not mean to slow down — or land — if they did mean to slow down.)
- What happens if a spacecraft in orbit reaches the escape velocity? (Answer: The spacecraft will overcome the Earth's gravity.)
- What do we call the point on an elliptical orbit that is furthest from the planet/Sun? (Answer: Apoapsis.)
- What do we call the point on an elliptical orbit that is closest to the planet/Sun? (Answer: Periapsis.)
- Two rockets have the same thrust force. Rocket A is half the mass of Rocket B. If the thrust force is greater than the sum of each rocket's mass and drag force, which rocket will accelerate faster? How much faster will this rocket accelerate? (Answer: Rocket A will accelerate twice as fast as Rocket B according to Fnet = ma).
Using the Equations: Ask students to solve the following problem using the equations from the Lesson Background. A rocket's engine expels mass at a rate of 10 kg/s with an exhaust velocity of 3,000 m/s. Calculate the thrust produced from the rocket. Express your answer in scientific notation. What is the specific impulse?
Answer:
Lesson Extension Activities
Besides circular and elliptical orbits, there are also parabolic and hyperbolic orbits. Have students research these types of orbits to determine what is special about them and how they are used.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students acquire a basic understanding of the science and engineering of space travel as well as a brief history of space exploration. They learn about the scientists and engineers who made space travel possible and briefly examine some famous space missions.

Students explore motion, rockets and rocket motion while assisting Spacewoman Tess, Spaceman Rohan and Maya in their explorations. First they learn some basic facts about vehicles, rockets and why we use them. Then, they discover that the motion of all objects—including the flight of a rocket and mo...

Students learn how rocket thrust is generated with propellant. The two types of propellants are discussed—liquid and solid—and their relation to their use on rockets is investigated. Students learn why engineers need to know the different properties of propellants.

Through the continuing storyline of the Rockets unit, this lesson looks more closely at Spaceman Rohan, Spacewoman Tess, their daughter Maya, and their challenges with getting to space, setting up satellites, and exploring uncharted waters via a canoe. Students are introduced to the ideas of thrust,...
References
National Aeronautics and Space Administration, Mars Exploration Program, http://mars.jpl.nasa.gov
National Aeronautics and Space Administration, Space Place http://spaceplace.nasa.gov/how-orbits-work/
Wertz, James R. and Larson, Wiley J. Space Mission Analysis and Design, 3rd Edition, Space Technology Library, Volume 8, New York, NY: Springer Publishing Company, 1999.
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Geoffrey Hill; Daria Kotys-Schwartz; Chris Yakacki; Janet Yowell; Malinda Schaefer ZarskeSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: June 1, 2021









User Comments & Tips