Summary
Students measure the relative intensity of a magnetic field as a function of distance. They place a permanent magnet selected distances from a compass, measure the deflection, and use the gathered data to compute the relative magnetic field strength. Based on their findings, students create mathematical models and use the models to calculate the field strength at the edge of the magnet. They use the periodic table to predict magnetism. Finally, students create posters to communicate the details their findings. This activity guides students to think more deeply about magnetism and the modeling of fields while practicing data collection and analysis. An equations handout and two grading rubrics are provided.Engineering Connection
In this activity, students characterize the field strength of a magnet as a function of distance. These types of experiments are done widely by national standards labs, third-party rating agencies, and component manufacturers (such as for magnets). These data are published in graphic and table forms in compilations such as the CRC Handbook of Physics and Chemistry. Then scientists and engineers refer to these publications as they design and determine specifications for parts and equipment.
Clinical engineers, for example, use these data to ensure no medical devices interact with others in such a way that makes erroneous readings or injures patients. Medical devices generate electromagnetic interference (EMI) that can affect the operation of other devices and implants such as cardiac pacemakers. EMI from hospital equipment and other sources such as cell phones, stereo headphones and even toys and jewelry that contain magnets can cause disturbances to pacemakers that currently have low resistance to EMI. Engineers examine magnetic field strength data to reduce patient risk by redesigning devices so they resist higher EMI levels or by designating separate high-EMI areas so people can avoid them—for example, creating “cell-phone zones” for phone use, instead of permitting phone use in patient rooms.
Clinical engineers also use these data to upgrade medical devices such as magnetic resonance imaging (MRI) machines to have lower magnetic field strength so they are safer for people with pacemakers.
Learning Objectives
After this activity, students should be able to
- Explain how permanent magnets work.
- Explain how a compass works.
- Explain that the magnetic field increases non-linearly as a permanent magnet is brought in from infinity.
- Identify the SI units of a magnetic field, often represented by the variable B and the unit tesla (T).
- Label the axis of a scatter plot with both physical meaning and units.
- Create an accurate scatter plot by hand or using a computing device.
- Manipulate a scatter plot to create a line of best fit, optionally using a computing device.
- Create a model and use it to make a prediction.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS1-1. Use the periodic table as a model to predict the relative properties of elements based on the patterns of electrons in the outermost energy level of atoms. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Use a model to predict the relationships between systems or between components of a system. Alignment agreement: | Each atom has a charged substructure consisting of a nucleus, which is made of protons and neutrons, surrounded by electrons. Alignment agreement: The periodic table orders elements horizontally by the number of protons in the atom's nucleus and places those with similar chemical properties in columns. The repeating patterns of this table reflect patterns of outer electron states.Alignment agreement: | Different patterns may be observed at each of the scales at which a system is studied and can provide evidence for causality in explanations of phenomena. Alignment agreement: |
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS2-6. Communicate scientific and technical information about why the molecular-level structure is important in the functioning of designed materials. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Communicate scientific and technical information (e.g. about the process of development and the design and performance of a proposed process or system) in multiple formats (including orally, graphically, textually, and mathematically). Alignment agreement: | Attraction and repulsion between electric charges at the atomic scale explain the structure, properties, and transformations of matter, as well as the contact forces between material objects. Alignment agreement: | Investigating or designing new systems or structures requires a detailed examination of the properties of different materials, the structures of different components, and connections of components to reveal its function and/or solve a problem. Alignment agreement: |
Common Core State Standards - Math
-
(+) Understand the inverse relationship between exponents and logarithms and use this relationship to solve problems involving logarithms and exponents.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Demonstrate the use of conceptual, graphical, virtual, mathematical, and physical modeling to identify conflicting considerations before the entire system is developed and to aid in design decision making.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
Texas - Science
-
Science concepts. The student knows the nature of forces in the physical world. The student is expected to:
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Scientific processes. The student conducts investigations, for at least 40% of instructional time, using safe, environmentally appropriate, and ethical practices. These investigations must involve actively obtaining and analyzing data with physical equipment, but may also involve experimentation in a simulated environment as well as field observations that extend beyond the classroom. The student is expected to:
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Scientific processes. The student uses a systematic approach to answer scientific laboratory and field investigative questions. The student is expected to:
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- lab notebook, one per student
- magnetic and non-magnetic materials, at least 2 of each per group; magnetic materials might include steel rods and metal nails; non-magnetic materials might include glass and plastic; (optional) include some fun magnetic materials, such as Crazy Aaron’s Strange Attractor Super Magnetic Thinking Putty with Magnet, one 3.2-oz tin for 2 or 3 groups, for $15 at https://puttyworld.com/products/strange-attractor-thinking-putty or Amazon.com
- a 3- or 4-inch compass with scales every 2 or 3 degrees; while a phone with a compass can be used, calibration may be a problem and a strong magnet may damage the phone
- a non-magnetic meter stick or paper scale ~30 cm in length
- graph paper
- a neodymium magnet; need not be very strong or large; ~2.2 cm/1-inch is adequate; a cube or cylindrical magnet is easier to work with than a disk-shaped magnet; available at Amazon.com or elsewhere, such as https://www.magnet4less.com/neodymium-magnets-1-2-in-x-1-in-diametrically-magnetized-cylinder
- (optional) clay, to hold the magnet in the desired orientation
- (optional) a way to create a semi-log plot, such as a calculator or a computer or tablet with Microsoft® Excel® or similar spreadsheet application
- a periodic table that shows electron configuration; such as the following good online resource at https://ptable.com/#Orbital
- Student Lab Notebook Rubric, one per student
- Proportional Magnetic Field Equations Handout, one per student
- Poster Grading Rubric, one per student
To share with the entire class:
- computers with Internet access
- large grid paper, such as a grid hand-drawn on butcher paper (using a ruler); on which to collect class data for all students to see
- (optional) tape, to adhere data and graphs into lab notebooks
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/rice_magnetic_activity1] to print or download.Pre-Req Knowledge
Students should be familiar with the basics of a compass (cardinal and ordinal directions, how it works) and magnets. They should also be able to graph a line of best fit and determine its equation (slope and y-intercept). Students should be able to interpret the periodic table and have an understanding of the basics of electron configuration, free electrons and spin.
Introduction/Motivation
How many of you have a cell phone? Stereo speaker headphones? An MP3 player or iPod? Did you know that these, along with other items we use in our everyday lives, can create magnetic fields? How do magnets work? (Let students explain. Foster a discussion. Student input might include: Magnets have two poles and can attract/repel magnetic material; free electron spin states align to create magnetism, etc.) A magnetic field is created by magnets; it is an invisible area around a magnet where objects may be affected by magnetic force.
Engineers use data related to magnetic fields to design and create new devices. Why might engineers be interested in knowing about magnetic field strength? (Expected responses might include: To determine the material to use for building, to conduct experiments in real-life scenarios, to prevent undesired interaction between devices, etc.)
Clinical engineers use these data when developing new equipment for use in hospitals. Medical equipment and implants can be very sensitive to electromagnetic interference (EMI), which can be caused by magnets within cell phones, toys, clothes and jewelry. It is important for clinical engineers to know the magnetic field strength of these magnets so that they can design equipment that limits erroneous readings due to EMI. Existing hospital equipment, such as magnetic resonance imaging (MRI) machines also create strong magnetic fields that can damage pacemakers and automated, implantable cardiac defibrillators (AICD). Clinical engineers refer to magnetic field data to develop new MRIs with lower magnetic field strength in order to decrease the risk to people with these implants.
Today, you will think like engineers to determine the magnetic field strength of a neodymium iron boron magnet. First, we will look into the chemistry behind magnets. (If students did not bring up free electrons and spin in the earlier discussion, introduce it now.) Whether a compound becomes magnetic is dependent on the free electrons of its atoms and their spin states, so that means we can use the periodic table to predict magnetism.
Then, we will use a compass to find the magnetic field strength of a magnet as a function of distance from the magnet and use these data to make a model of magnetic field strength. Like engineers, we will use that model to find the magnetic field strength at the edge of the magnet, which would interest clinical engineers as they create devices that might be placed in close proximity to one another.
Procedure
Background
A compass is an instrument that incorporates a permanent magnet and a scale labeled with cardinal directions such that the magnet lines up with the Earth’s magnetic field and the needle always points “north.” As the compass body is rotated, the needle remains fixed and the new direction of the compass is indicated. Since a compass merely points to the dominant magnetic field, additional magnetic fields will deflect the compass. Using certain assumptions and trigonometry, therefore, an external magnetic field can be approximated using a compass.
A magnetic field varies with the magnetization of the material and the distance from the center of the magnet. The magnetization depends on the elements that compose the magnet and the way the elements are joined. Magnetization is a result of the spin alignment of unpaired electrons in the atoms and the angular momentum of these unpaired electrons resulting from the shell; for the magnets used in this activity, neodymium-iron-boron (NdFeB), this is the f-shell. As such, the position in the periodic table can be indicative of which elements are magnetic.
Looking at the periodic table, one can see that iron (Fe) has an electron configuration of [Ar] 3d6 4s2 with four unpaired d-shell electrons, and neodymium (Nd) has an electron configuration of [Xe] 4f4 6s2 with four unpaired f-shell electrons. The online periodic table linked in the Materials List shows the formula of and a figure of electron configuration. Current studies in magnetism focus either on the d-shell electrons or the f-shell electrons since these shells can contain up to 10 and 14 electrons, respectively. Hund’s Rule and the Pauli Exclusion Principle lead to filling up the shells with unpaired electrons in the same spin state first, and then pairing those up with electrons having opposite spin. Because of the abundance of electrons able to fill the d- and f-shells, these shells tend to have more unpaired electrons than others, which leads to the atom expressing magnetic properties; for example, neodymium (Nd) provides a large magnetism due to free f-shell electrons.
This activity guides students to think more deeply about magnetism and the modeling of fields while practicing data collection and analysis. A strong NdFeB magnet is used for dramatic effect and to enable relationships to form using the periodic table.
When students calculate the approximate magnetic field of a magnet, the approximation depends on the external magnetic field generated by the magnet being perpendicular to the Earth’s magnetic field. This is done by orienting the compass north-south and then aligning the magnet along the east-west axis. The magnet must be oriented so the compass deflects in a circular fashion and not up and down (indicating that magnet may not be in a stable orientation). If the magnet is not in a stable orientation, use clay to stabilize the magnet.
The magnetic field data generated in this lab is a non-linear curve on a scatter plot. For most students, differentiating a linear and non-linear function, and making some statements about the rate of change is sufficient. However, you can lead students to take it further, assuming the curve can be modeled as a power function:
B=aXn
where a and n are real constants. B is the proportional magnetic field B ⍺ tan(θ), where θ is the angle recorded by students, and X=d, the recorded distance.
This function can be linearized by taking the log of both sides:
log(B)=log(aXn)
which results in the linear function:
log(B)=log(a) +nlog(X)
Therefore, if you plot log(B) versus log(X) on a scatter plot, the slope of the line of best fit will be the power n, and the y-intercept will be the constant multiplier.
This linear fit will likely be accurate to one significant figure and can be used for an order of magnitude calculation. For instance, using the magnetic field results approximated above, you can solve for the proportional magnetic field at the magnet edge by setting the equation to the distance at the edge of the magnet. This, again, will just be an order of magnitude calculation, but results in a value that cannot be measured easily. Engineers refer to these data when constructing devices with many magnetic parts that might interfere with each other. They need a model to determine the magnetic field strength at the edge of the magnetic part when they are attempting to place another part very close to it.
During the activity, students are asked to create a line of best fit for a log-log plot. To do this, they must know how to calculate the log of a number using a calculator or a spreadsheet program such as Microsoft® Excel®. They must be able to draw a line of best fit or use a computer application to generate a line of best fit. On most spreadsheets, the function “linest” generates a slope and y-intercept. To create a line of best fit by hand, students need to draw a straight line through the data. In this case, the object is not to “connect the points.” The line should have an equal number of points above and below, with the line not necessarily crossing though any points. The line should incorporate all points, and cross the y-axis.
Before the Activity
- Gather materials and make copies of the Student Lab Notebook Rubric, Proportional Magnetic Field Equations Handout and Poster Grading Rubric.
- Prepare (or have students prepare) a large sheet of graph paper to record class data points as a scatter plot, as shown in Figure 2. This is also the same format that students use for their individual graphs.
With the Students
- Present to the class the Introduction/Motivation content, including an opening discussion that serves as a pre-assessment review of concepts relating to magnets and magnetism.
- Hand out copies of the lab notebook rubric and go over the activity expectations with students.
- Have students look up the words magnet, magnetism, magnetization and magnetic field, and write a summary of their definitions in their lab notebooks. In particular, direct students to relate the magnetic field to another field they know about, such as the electric and mass force fields. Discuss as a class.
- Tell students that a strong magnet is composed of neodymium (Nd), iron (Fe) and boron (B)—an NdFeB magnet. Show students or give them access to a periodic table so they can discuss magnetic and non-magnetic items, including free electrons and shells. Have students look at unpaired electrons in Nd compared to Fe and B through the electron configuration of each atom. Discuss as a class.
- Demonstrate how much force is needed to detach neodymium magnets. To demonstrate the attraction force, bring one neodymium magnet close to another without touching them together. An exact force value need not be calculated, but give a general idea of strength so students are warned against putting two magnets together.
- Organize the class into groups of four students each.
- Distribute the neodymium magnets and magnetic/non-magnetic materials to each group. Have students generate some ideas about why some objects are affected by or produce magnetic fields while other materials do not. (If you provide students with the [optional] magnetic putty, explain a few putty activities or play them a few online videos to show them what can be done with it, such as the short videos listed in the Additional Multimedia Support section.) Discuss findings as a class.
- Hand out to each group a neodymium magnet and a compass. Direct the teams to each determine the magnet orientation that deflects the compass when the compass is initially set pointing north. For example, the magnet shown in Figure 1 would not deflect the compass if rotated 90 degrees from the orientation shown. Flip the magnet around until the compass deflects towards the magnet.

- Hand out to each group a meter stick or paper scale.
- Have students determine the orientation of the scale (east or west) so that the compass deflects to the east (be prepared to show them or demonstrate the setup in Figure 1). When the magnet is brought close to the compass (as shown in Figure 1), the arrow deflects to the west. Notice the degree measurements go down from 360 in westward deflection. Changing the compass orientation so the arrow deflects towards the east yields degree measurements from 0, which makes calculations easier. (If some groups’ magnets roll away when in the correct orientation, have them use clay to keep the magnets in place. Demonstrate this by putting a bit of clay around a magnet so that it does not move from its desired orientation when placed on the table.)
- Direct the teams to set up their compasses so that they point north, which will be considered 0°.
- Tell them to set the center of the compass at the zero of scale.
- Direct the students to sketch in their lab notebooks the compass, magnet and scale in its initial orientation. An example initial setup is shown in Figure 1A.
- Direct students to record the maximum and minimum distances for the magnets. The maximum distance is where the compass just deflects from north. The minimum distance is where the deflection is between 70° and 80°. See Figure 1A, 1B and 1C for examples. Have groups record the distance (to the center of the magnet) in meters or centimeters and the deflection in degrees.
- Direct students to return the magnet to the minimum distance. Have students bring the magnet closer and record the distance and deflection until five distance/deflection pairs are recorded per group. Have each group member record the data in his or her own notebook. Remind students that their data must be taken from between the minimum and maximum distances.
Conversion to Proportional Magnetic field
- Tell students that the magnetic field of the compass is proportional to the tangent of the deflection, and have them use a calculator or spreadsheet application to calculate the tangent of the angle for each measurement.
- Have groups plot the distance (x-axis) and tan(θ) (y-axis, representing the proportional magnetic field strength) for each data point on the large grid paper for the class (see Figure 2).
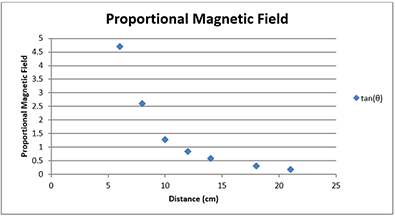
- If the data do not follow an exponential curve, or one or more data are way off the curve, have students document this in their notebooks, develop a new procedure to take data (if necessary), and generate a new data set.
- On their own graph paper, have each student create (by hand) a scatter plot of the group data after the data has been validated on the large grid paper. Instruct students to use the large scatter plot as a model.
Calculations
- Distribute copies of the equations handout. Show students the equations relating proportional magnetic field strength to distance. Explain that data are easier to analyze when in linear form, and then show them the log equation. For each distance and proportional B value, have students determine the log. Direct students to do this by hand or by using a spreadsheet or other tool.
- Instruct students to graph the log(distance) and log(tan(θ)) data (it should be a line, more or less), either by creating hand-drawn or spreadsheet graphs (the method determined by the teacher).
- Tell students to create a line of best fit, either by hand or by using spreadsheet software on a computer or tablet. If using a spreadsheet application, use the “linest” or trendline function to calculate the slope and y-intercept. If doing by hand, direct students to draw a line through the data.
- If the line of best fit was generated by a computer, have students graph the line of best fit on the scatter plot and use the software to display the equation of the best fit line to determine the slope and the y-intercept. If the line was generated by hand, have students calculate the slope and y-intercept.
- Have each student sketch or tape a copy of the data and the line of best fit in his or her lab notebook, report the slope and y-intercept, and write the linear equation for the graph.
- Direct students to calculate the magnetic field strength at the magnet edge, using the linear equations they developed. If students have trouble, tell them the x-value is the distance from the center of the magnet, so use the radius of the magnet to represent the magnet edge. After solving the linear equation, remind students to take the inverse log of it to determine the resulting proportional magnetic field (remind students that they took the log of their magnetic field strength equation to linearize it).
- To conclude, guide students through the poster-creating post-assessment, as described in the Assessment section.
Vocabulary/Definitions
compass: A permanent magnet set to align with a magnetic field.
deflection: The degree to which an element is displaced under some force.
log-log plot: A plot in which both axis are scaled as a log function instead of a linear function.
magnet: A material that produces a magnetic field.
magnetic field: A vector force field that is produced by moving electrons or intrinsic magnetic moments of elementary particles.
magnetization: The density of permanent or induced magnetic moments in a material.
scatter plot: A plot that graphs two quantitative variables against two orthographic axis, one dependent, the other independent, as discrete points, sometimes connected by line segments. Also called a scatter graph or scatter chart.
Assessment
Pre-Activity Assessment
Review: During the presentation of the Introduction/Motivation content, evaluate student contributions and base knowledge during the discussion reviewing magnets and magnetism.
Activity Embedded Assessment
Procedure and Data Documentation in Lab Notebooks: During the activity, have students detail in their lab notebooks the procedure they use to collect data, including the process they use to take accurate angle measurements. Require them to each include a neat data table and scatter plot. Examine the scatter plot and log-log plot, including looking for correctly scaled and labeled axes and units, as the primary assessment. The data for the scatter plot should not be linear. The data for the log-log plot should be reasonably linear with a reasonable line of best fit. Expect students to write-out a correct linear equation and use it to solve for the magnetic field at the magnet edge. Use the Student Lab Notebook Rubric as a guide for grading student lab notebooks.
Post-Activity Assessment
Summarizing Poster: Assign each group (or individual student) to make a poster about the activity and their findings. Use the Poster Grading Rubric to evaluate the posters. Explain to students the (suggested) poster section and content requirements provided below (which are also mapped to the rubric):
- Introduction: Describe an NdFeB magnet. Explain why the magnet had to be oriented in a certain way. Explain how a compass indicates the change in magnetic fields. Optional: include an activity-related picture.
- Methods: Explain how the experiment was set up and conducted in order to obtain accurate data. Optional: include pictures of work being done.
- Data: Include the scatter plot here, along with text explaining how the data was transformed and why it is non-linear.
- Results: Put the log-log plot here. Explain why the plot was created. Use the radius of the magnet to calculate the magnetic field at the edge of the magnet.
- Discussion: Explain how data was transformed to the scatter plot and then to the log-log. Explain how and why it was necessary to use the equation to calculate the magnetic field at the edge of the magnet instead of simply measuring the value. Justify the calculated value as reasonable and possible. Describe what other work could/should be done to extend this research.
- Conclusions: Explain the activity purpose, including how the results might be used in real-life engineering. If desired, have students conduct online research to discover additional engineering connections and applications.
- Acknowledgements: Mention anyone who helped with the activity, and list citations for any references used.
Investigating Questions
- What is a field and how does studying fields help us study physics and engineering? (Answer: Fields give the value at each point in space and time for a physical quantity. They are used to explore the effects of that quantity on nearby objects.)
- What are we referring to when we talk about a magnetic field? (Answer: The area surrounding a magnetic object where the magnetic force acts.)
- From where does a magnetic field come? (Answer: The spin states of free electrons aligning create a magnetic field.)
- Do locations exist around a magnet where the magnetic field is constant? (Answer: At points that are equal distance away from the magnet, the magnetic field is considered constant.)
- Is the magnetic field constant everywhere? (Answer: No, field strength depends on distance from the magnet.)
- Would our data be different if we traveled to a place where the magnitude of the Earth’s magnetic field was the same, but north was in a different direction? (Answer: If we do not reset the experiment with the new north, the angle measurements would differ; however, relationships between tanθ, distance and magnetic field would be the same.)
Safety Issues
Neodymium magnets are very strong. If two stick together or if one is stuck to a surface, removal can cause injury, most commonly pinched skin. So, advise students to not play with their magnets or put two magnets together.
Do not use metal or other magnetic material for the experiment; the magnets are strong and can magnetize a material such as a metal ruler, which invalidates the results.
For this introductory activity, weaker magnets may be used. The magnets must register a wide deflection (5°-70°) for reasonable distances. Small permanent magnets like “buckyballs” are not recommended. It is best if the magnets are large enough to easily be kept track of and able to generate a large enough magnetic field so students can collect good data.
Troubleshooting Tips
- Keep magnets separated.
- Do not use metal materials that attract the magnets.
- If students use phones for compasses, have them keep the magnet far away, then calibrate the phone, then set up the experiment. If a problem is encountered with the compass on the phone, the phone must be recalibrated and the experiment must be restarted from the beginning.
- A phone can be damaged by a strong permanent magnet, so if a phone is being used, keep the magnet from touching the phone by placing a barrier around the phone to keep the magnet several centimeters away.
- If the magnetic compass is acting flaky, remove it, tap it gently, and begin the experiment again.
- Try different magnet orientations to maximize deflection and minimize the needle moving up and down. Use clay to fix the magnet orientation.
- Part of the reason to plot data as a group is so teams with inaccurate data will see that their data does not fit the curve. Have these groups take their data again, with more care.
- When finding the tangent of the angle of deflection, put calculators in the “degrees” mode, while the spreadsheet function might require the angle to be in radians. Convert if necessary using: radians = (degrees) * (π/180).
Activity Extensions
The values calculated from the compass deflection are proportional to the magnetic field generated by the magnet at a certain distance. Many engineers are interested in the value of the magnetic field generated by the magnet alone, which is a concern when developing new devices that might interact with existing ones (such as any new equipment to be placed in hospital rooms). To determine the value of the magnetic field, we need to make certain assumptions (primarily that the magnetic field of the magnet is perpendicular to the magnetic field of the Earth as measured by the compass) and we must know the magnetic field of the Earth at the location where we are conducting the experiment, or more precisely the component of the magnetic field that the compass is measuring. An approximation can be found at the following NOAA website: https://www.ngdc.noaa.gov/geomag-web/#igrfwmm; given a zip code or location, it provides the magnetic field for the day. For our purposes, we are interested in the horizontal component.
For the first extension activity, have students multiply the value of the Earth’s magnetic field by tan(𝝷) to determine an approximate value for the magnetic field generated by the magnet alone (excluding the magnetic field of the Earth). Again, this is only an approximation.
As a follow-up extension, have students graph the values generated.
Activity Scaling
- For lower grades, generate the graphs as a class.
- For more advanced students, have them determine the electron configuration on their own or in groups. This can be done by referring to the periodic table to find the number of electrons as a starting point, and then “filling up” the orbitals. Refer to a website link in the Additional Multimedia Support section that explains this process.
- For more advanced students, give them only the initial power equation relating proportional magnetic field and distance, and have them derive the linear equation on their own or in groups.
Additional Multimedia Support
- Magnetic field database and calculators: https://www.ngdc.noaa.gov/geomag-web/#igrfwmm
- Unpaired electron table: https://upload.wikimedia.org/wikipedia/commons/2/25/Periodic_Table_with_unpaired_electrons.svg
- Crazy Aaron’s Thinking Putty Review video (9:44 minutes): https://www.youtube.com/watch?v=BlW-y156KuM
- If you provide students with the (optional) magnetic putty, explain a few putty activities or play them a few online videos to show what can be done with it, such as https://www.youtube.com/watch?v=ZXJuJQVrgbI (1:16 minutes) and https://www.youtube.com/watch?v=DBrkHgpTBA4&feature=youtu.be (1:34 minute)
- For more advanced students, refer to this electron configuration explanation: https://chem.libretexts.org/Core/Physical_and_Theoretical_Chemistry/Electronic_Structure_of_Atoms_and_Molecules/Electronic_Configurations/Electronic_Configurations_Intro
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students investigate the properties of magnets and how engineers use magnets in technology. Specifically, students learn about magnetic memory storage, which is the reading and writing of data information using magnets, such as in computer hard drives, zip disks and flash drives.

Students are introduced to the effects of magnetic fields in matter addressing permanent magnets, diamagnetism, paramagnetism, ferromagnetism and magnetization.

Students are briefly introduced to Maxwell's equations and their significance to phenomena associated with electricity and magnetism. Basic concepts such as current, electricity and field lines are covered and reinforced. Through multiple topics and activities, students see how electricity and magne...
References
Allain, Rhett. Published January 21, 2014. “How Do You Measure the Magnetic Field?” Wired, Conde Nast Digital. Accessed July 15, 2015. https://www.wired.com/2014/01/measure-magnetic-field/
Beinart, Roy, and Saman Nazarian. Published 2013. “Effects of External Electrical and Magnetic Fields on Pacemakers and Defibrillators: From Engineering Principles to Clinical Practice.” Circulation, PubMed Central, Vol. 128, No. 25, pp. 2799–2809. Accessed August 2, 2016. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3908865/
Clinical Engineering Handbook, ed: Joseph F. Dyro. Chapter 60: Interactions between Medical Devices, page 249 (engineers use magnetic field strength in medical devices, Medical Devices Testing). Amsterdam, The Netherlands: Elsevier Academic Press, 2004. https://books.google.com/books/about/Clinical_Engineering_Handbook.html?id=EIeQhdrW2VMC and http://tinyurl.com/jrouu8y
Hodgman, Charles D., Melville F. Coolbaugh, and Cornelius E. Senseman. Handbook of Chemistry and Physics: A Ready-Reference Pocket Book of Chemical and Physical Data, 8th edition. The Chemical Rubber Company, Cleveland OH; Norwood, MA: The Plimpton Press, 1920. Accessed July 15, 2015. https://ia800904.us.archive.org/19/items/HandbookOfChemistryAndPhysics8thEd.1920/HandbookOfChemistryAndPhysics8thEd.TheChemicalRubberCompany1920-n.pdf
Lunk, Brandon, and Robert Beichner. Published January 2011. “Exploring Magnetic Fields with a Compass.” The Physics Teacher, North Carolina State University, Vol. 49. Accessed July 15, 2015. http://www.ncsu.edu/per/Articles/LunkBFieldArticle.pdf
Reference Data for Engineers: Radio, Electronics, Computer and Communications, 9th edition, ed: Mac E. Van Valkenburg and Wendy M. Middleton. Chapter 12: Measurements and Analysis, page 12-36 (how do engineers use magnetic field strength to design equipment; clinical engineers and magnetic interference). Boston, MA: Newnes, 2002. Accessed July 15, 2015. https://books.google.com/books?id=R67HARlhisYC&dq=how+do+engineers+use+magnetic+field+strength+to+design+equipment&source=gbs_navlinks_s and http://tinyurl.com/js4fvzo
Copyright
© 2016 by Regents of the University of Colorado; original © 2015 Rice UniversityContributors
Ralph Cox; Sabina SchillSupporting Program
Nanotechnology RET, Department of Earth Science, School Science and Technology, Rice UniversityAcknowledgements
This material was developed in collaboration with the Rice University Office of STEM Engagement, based upon work supported by the National Science Foundation under grant no. EEC 1406885—the Nanotechnology Research Experience for Teachers at the Rice University School Science and Technology in Houston, TX. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation or Rice University.
Special thanks to Emilia Morosan, Jessica Santiago and Eteri Svanidze at Rice University for their guidance and patience.
Last modified: February 13, 2020









User Comments & Tips