Lesson Magnetic Fields Matter

Learning Objectives

After the lesson, students should be able to:

• Describe the magnetic field and causes of a permanent magnet.
• Compare and contrast paramagnetism, ferromagnetism and diamanetism.
• Calculate the net magnetization of an object.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

NGSS: Next Generation Science Standards - Science

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Worksheets and Attachments

Introduction/Motivation

In order to understand the MRI and determine safety hazard differences, we must understand the differences between diamagnetic, paramagnetic and ferromagnetic materials. We must also understand the other effects of magnetic fields in matter. Engineers who design medical equipment are always comparing and contrasting safety hazards in order to ensure safe working and diagnostic environments for people.

Lesson Background and Concepts for Teachers

Legacy Cycle Information

This lesson fits into the research and revise phase of the legacy cycle during which students are provided with additional information enabling them to revise their initial ideas for solving the challenge. The research aspect consists of lecture on the effects of magnetic fields in matter including diamagnetism, paramagnetism, ferromagnetism and magnetization.

Information: Magnetic Fields in Matter

Consider the magnetic field around and inside a solenoid compared to the field inside and around a permanent magnet as shown in Figure A.

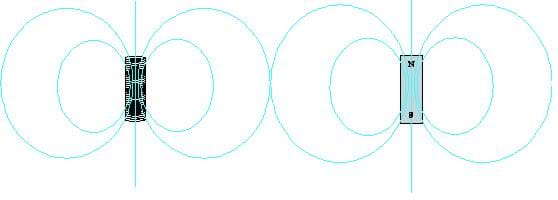
The fields are similar enough that one is tempted to think of the permanent magnet as a solenoid. In practice, this approximation is fairly accurate, that is, to think of the magnet as comprised of many current loops. However, unlike the solenoid, the permanent magnet does not consist of current loops around the outside of the volume, but a multitude of tiny current loops inside the material. Instead of actual current loops, these are atoms, consisting of a positive nucleus, and electrons that are in motion, which may be loosely considered something of an orbit about the nucleus. Although this is not a current loop in the strictest sense, and is a purely quantum mechanical phenomenon, electrons and atoms as a whole can resemble loops of current in the sense that they have a magnetic moment and experience a torque in a magnetic field, and also can produce magnetic fields of their own.

The electrons in an atom can exhibit a magnetic moment in two ways. One is that the motion of the electron near the nucleus, which can semi-classically be thought of as a sort of orbit, generates a magnetic moment. The other way, which is often more puzzling to students new to quantum mechanics, is that electrons and other point particles possess an intrinsic magnetic moment known as "spin." Imagine a sphere of charge spinning like a top, and hence, creating a loop of current and a magnetic moment along the axis of rotation, but this model would not make much sense for a particle that does not take up any space. The best way to understand spin is to take a few courses in quantum mechanics, but for the moment just accept that these particles possess an intrinsic magnetic moment for purely quantum mechanical reasons.

In atoms, electrons tend to "pair up" to cancel out each other's spin moments, resulting in the rule of thumb that atoms with an even number of electrons tend to not have much of an overall magnetic moment. Atoms with an odd number of electrons do tend to have a permanent magnetic moment. However, atoms generally tend to be randomly oriented, so all the small fields produced in a solid generally cancel out, which is why most objects around us do not produce permanent magnetic fields.

Diamagnetism

Diamagnetism is a property exhibited by all solid materials. Even if atoms have no permanent magnetic moment, or if the magnetic moment is randomly oriented, atoms do possess electrical charge. By Faraday's law of induction and Lenz's law, when an object consisting of atoms is placed in a field, there will be a small induced magnetic moment opposing the field. This causes a diamagnetic material to be repelled from a magnetic field. The induced moment is extremely small, and so diamagnetism is a very weak effect that can barely be observed.

Paramagnetism

Many atoms have a permanent magnetic moment, usually due to unpaired spins, which could be due to an odd number of electrons or other reasons. For most materials, these moments do not interact with the fields from other atoms, and so the moments are all randomly oriented and cancel out, leaving no total magnetic moment for a solid. However, if the solid is placed in an external magnetic field, the atoms experience a torque aligning the moments to the field. The permanent moments are generally much stronger than the moments induced by Faraday's law, so diamagnetic effects can generally be ignored in these solids. As a result, the aligned moments create an overall moment and a field in the same direction as the external field, and the material is attracted to the magnetic field.

When the magnetic field is removed, the arrangement immediately dissolves and the field produced by the paramagnet disappears. In addition, usually enough thermal energy exists within the paramagnet to ensure that only a very small number of the atomic moments line up with the field at any given time, so the effects of paramagnetism are quite weak.

Ferromagetism

A few materials, such as iron, cobalt and nickel, have permanent magnetic moments and also have the property that the magnetic moments in each atom interact with each other, causing them to naturally align in the same direction. Most chunks of iron or other ferromagnetic materials consist of microscopic domains consisting of many atoms that are aligned in the same direction. Inside a domain is a net magnetic field, but the domains themselves are randomly oriented and so the overall fields in the solid tend to cancel out. For this reason, most iron objects do not possess an overall magnetic field. When a ferromagnetic object is placed in a magnetic field, domains aligned with the field are preferred, and so those domains tend to grow, appropriating atoms along the borders of the domain. In addition, domains as a whole may rotate towards the field. This causes the ferromagnetic material to produce a fairly strong field in the direction of the applied field, and so a ferromagnetic material is be strongly attracted to an applied field and rotates to the direction of the field. The alignment within the ferromagnet is strong enough that it may be much greater than the applied field.

Even when the applied field is removed, a residual effect exists on the domains of the material, so that the material may retain a "permanent" field, which is the source of the term "permanent magnet." The maximum amount of field that can be produced by the alignment of the moments in a ferromagnetic material is called the saturation point.

In general, the field produced by a ferromagnet depends not only on the applied external field, but also on the magnetic "history" of the fields that have been applied in the past.

Magnetization

No matter what mechanism causes a solid to respond to a field, we can still measure how it responds to a magnetic field by looking at the net magnetic moment per unit volume of the material. This quantity will be a vector as there is a direction to the magnetic moment and also a magnitude, that is

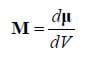
This quantity can be understood by comparison to a tightly wound solenoid. The effect of the magnetization is no different than if the magnet was a solenoid carrying a current per unit length of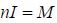

Either way, we would find the same dipole moment. The magnitude of the field inside a tightly wound solenoid is

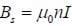
so the field inside an object with magnetization M has a magnitude of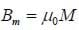

If we put a material into an applied uniform field, the total field inside the object would then be

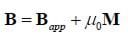
The two vectors M and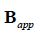

will be parallel in paramagnets and ferromagnets, and antiparallel in diamagnets. In a ferromagnet this magnetization depends on the previous fields that the material has been exposed to, as this "history" of the object will have affected the domains. However, in most materials, that is diamagnets and paramagnets, the magnitude of M is a linear function of the magnitude of the applied field. Since the magnetization of these materials is zero when no field is applied, the magnetization and induced magnetic field will be directly proportional to the applied field. Thus we can write,

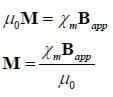
where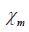

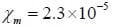
and in copper, which is diamagnetic,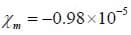

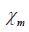
can generally not be considered constant or even well defined in the case of no applied field, but if calculated empirically for a given object and applied field, values would ranging from several hundred to 100,000.

There is however, generally a maximum value of 8 for ferromagnetic materials. In addition, ferromagnetic materials have a maximum magnetization

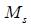
which corresponds to the total alignment of all magnetic moments in the solid. In annealed iron, this value is high enough so that

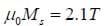
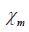
may range into the thousands, the applied field needed to saturate this piece of iron could be lower than 100 Gauss. Typically, to create a strong electromagnet, one places an iron core inside of the solenoid or toroid, and the field generated by the current may be boosted several hundred times by the field produced in the iron.

For whatever historical reason, there are two more terms in common, which although generally unnecessary, do help simplify the equations slightly.

The relative permeability is defined as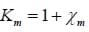

and the permeability is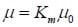

For diamagnetic and paramagnetic materials, the relative permeability wis approximately 1 and so the permeability is approximately the same as the permeability of free space.

Assessment

Homework

Homework: Have students complete the Magnets in Matter Homework questions as a take-home assignment. Review their answers to assess their progress with the concepts of diamagnetism, paramagnetism, ferromagnetism and magnetization.

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.