Quick Look
Grade Level: 12 (11-12)
Time Required: 45 minutes
Lesson Dependency:
Subject Areas: Physics
NGSS Performance Expectations:

| HS-PS3-2 |
Summary
Beginning with a class demo, students are prompted to consider how current generates a magnetic field, and the direction of the field that is generated. Via a lecture, students learn Biot-Savart's law (and work some sample problems) in order to calculate, most simply, the magnetic field produced in the center of a circular current carrying loop. For applications, students find it is necessary to integrate the field produced over all small segments in a current-carrying wire.Engineering Connection
It is important that engineers know and understand how a looped wire can create a current so that imaging techniques such as MRIs can be as accurate as possible without physically harming people. During their lesson homework, students use the Biot-Savart law to find the magnitude and direction of a magnetic field due to current in a looped wire.
Learning Objectives
After the lesson, students should be able to:
- Explain that current creates a magnetic field.
- Use the Biot-Savart law to integrate and find the magnetic field of current carrying wire.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS3-2. Develop and use models to illustrate that energy at the macroscopic scale can be accounted for as either motions of particles or energy stored in fields. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Develop and use a model based on evidence to illustrate the relationships between systems or between components of a system. Alignment agreement: | Energy is a quantitative property of a system that depends on the motion and interactions of matter and radiation within that system. That there is a single quantity called energy is due to the fact that a system's total energy is conserved, even as, within the system, energy is continually transferred from one object to another and between its various possible forms. Alignment agreement: At the macroscopic scale, energy manifests itself in multiple ways, such as in motion, sound, light, and thermal energy.Alignment agreement: These relationships are better understood at the microscopic scale, at which all of the different manifestations of energy can be modeled as a combination of energy associated with the motion of particles and energy associated with the configuration (relative position of the particles). In some cases the relative position energy can be thought of as stored in fields (which mediate interactions between particles). This last concept includes radiation, a phenomenon in which energy stored in fields moves across space.Alignment agreement: | Energy cannot be created or destroyed—it only moves between one place and another place, between objects and/or fields, or between systems. Alignment agreement: |
Common Core State Standards - Math
-
Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Energy can be grouped into major forms: thermal, radiant, electrical, mechanical, chemical, nuclear, and others.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Assess how similarities and differences among scientific, mathematical, engineering, and technological knowledge and skills contributed to the design of a product or system.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
National Science Education Standards - Science
-
Results of scientific inquiry--new knowledge and methods--emerge from different types of investigations and public communication among scientists. In communicating and defending the results of scientific inquiry, arguments must be logical and demonstrate connections between natural phenomena, investigations, and the historical body of scientific knowledge. In addition, the methods and procedures that scientists used to obtain evidence must be clearly reported to enhance opportunities for further investigation.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/van_mri_lesson_5] to print or download.Pre-Req Knowledge
This lesson discusses the Biot-Savart law, which gives a way to integrate and find the magnetic field created by a loop or segment of wire. Thus, students must understand the basics of integration.
Introduction/Motivation
Engineers try to be as accurate as possible when designing MRI machines by understanding how looped wires affect magnetic fields. A significant portion of some engineers' jobs is to educate surgeons and radiologists about MRI accuracy. For example, to prevent irreversible damage to a patient with a brain tumor, it is crucial that the surgeon remove only the damaged tissue and avoid removing or coming into contact with healthy tissue.
Class Demonstration: Magnetic Field around a Current-Carrying Wire
Objective: Use this class demo to guide students to think about how current generates a magnetic field, and the direction of the field that is generated.
- 14-gauge magnet wire, 200 - 600 feet
- 30W or higher 5V DC power supply, 1-3
- 1 lab stand
- iron filings, 1 oz
- cardboard, 2 sheets, for holding the filings
- 1 roll tape
- compass, 6-10
The basic idea for this demo was conceived by William J. Beaty who wrote:
"A number of science museum exhibits require many tens of amperes of electric current in a thick cable to generate strong magnetism. One example is a raft of compasses with a 200-amp cable running through the center of the raft. Or, three 100-amp cables with three-phase AC powering them, where the resulting field rotates and can spin a conductive object by induction.
Rather than trying to build a 2-volt, 200 ampere supply, there is an easier way. Think:
In stranded cable, the DC electric current divides equally among all the strands.
If a 200-amp cable has 200 strands, then each strand has only 1.0 ampere. So instead of using a length of thick cable, why not wind a hoop-coil of very large diameter? (For example, a hoop that is 3 ft in diameter.) Wrap the coil with black electrical tape so that it resembles a circle of heavy black cable. Send 1.0 amperes into the coil's connections, and you have a circular "cable" that has 1 ampere within each "strand," and 200 amperes within the cable as a whole. There is no difference between a segment of this "coil" and a segment of a thick electrical cable with an enormous current inside."
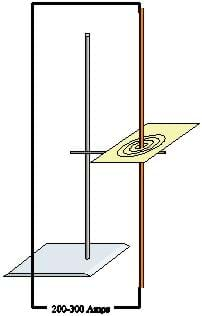
For this demo, making a coil with a diameter of 1.5 feet using 14 gauge wire and wrapping 20 turns makes a coil with a resistance of 1 ohm. This can be connected to the 5 volt power supply and attached to the lab stand so that a portion of the wire is directed straight up and down, as shown in Figure 1. The resulting current will be 100 amps. You will get a stronger effect if you repeat this process and tape together 2-3 cables, although even one produces an observable effect.
To begin the demonstration, have students hold magnets close to the wire in a circle with the current turned off. Make sure the compasses are all pointing in the same direction. Turn on the current and the compasses will point around the wire. Then reverse the direction of the current and the compasses will reverse directions.
Next, place a cardboard sheet horizontally around the wire as shown in Figure 1 (you will need to have punched a hole in the sheet). Sprinkle iron filings around the wire and turn on the current. You may need to shake the cardboard sheet. Then watch the filings align into concentric circles. Discuss with the class the direction and strength of the field produced, noting that the magnetic field forms closed circles around the wire.
Lesson Background and Concepts for Teachers
Legacy Cycle Information
This lesson fits into the research and revise phase of the legacy cycle during which students are provided with additional information enabling them to revise their initial ideas for solving the challenge. The research aspect consists of a demonstration of the magnetic field around a current-carrying wire as well as lecture on the Biot-Savart law. The lecture includes example problems for the teacher to work through with the students.
Biot-Savart Law
As was seen in the demonstration, an electric current produces a magnetic field. Consider a small segment of wire with length dl carrying a current I. We can make dl into a vector dl by giving it the direction in which the current is flowing. This small segment produces a small magnetic field dB at a point P whose magnitude and direction are given by the following equation, known as the Biot-Savart law (pronounced with silent Ts.)
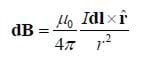
The symbol 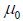
represents a constant called the permeability of free space and in standard units is:
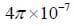
For any real application, it will be necessary to integrate the field produced over all of these small segments in an actual current carrying wire. The simplest example is the magnetic field produced in the center of a circular current carrying loop. Another good example is a straight segment of wire.
Example:
Find the magnitude and direction of the magnetic field at the center of a loop carrying a current I with radius R.
Solution:
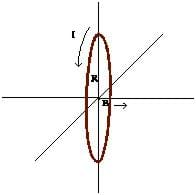
Note that for any choice of dl around the ring, dl is perpendicular to r and by the right hand rule, dB will point out along the axis of the ring.
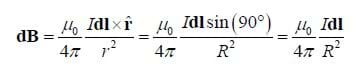
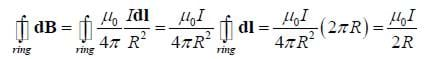
This is a relatively simple example as the integral is a constant. It is also not unreasonable to find the strength and direction of the magnetic field along the axis of the ring (see Homework in the Assessment section).
Example: Find the magnitude and direction of the magnetic field at some point P produced by a straight segment of wire along the x-axis from some point 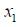
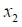
Solution: Start with the diagram shown below. Note that we will represent the angle between a segment I dl at some point x and r by 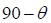
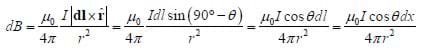
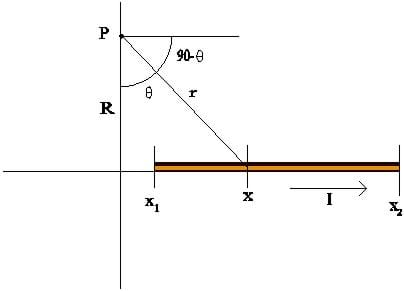
Then we may integrate from 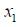
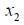
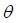
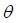
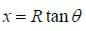
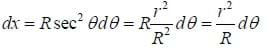
Then substituting, we see that:
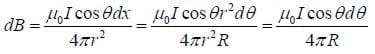
Now taking 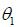
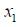
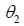
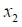
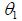
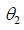
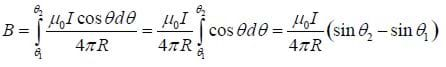
Finally, if the wire is extremely long, then 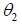
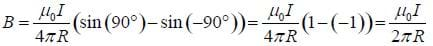
Assessment
Homework: Have students complete the Biot-Savart Law Homework questions as a take-home assignment. Review their answers to assess their progress in understanding the concepts.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

A class demo introduces students to the force between two current carrying loops, comparing the attraction and repulsion between the loops to that between two magnets. After a lecture on Ampere's law (including some sample cases and problems), students begin to use the concepts to calculate the magn...

After a demonstration of the deflection of an electron beam, students review their knowledge of the cross-product and the right-hand rule with example problems. Students apply these concepts to understand the magnetic force on a current carrying wire. Through the associated activity, students furthe...

Students induce EMF in a coil of wire using magnetic fields. Students review the cross product with respect to magnetic force and introduce magnetic flux, Faraday's law of Induction, Lenz's law, eddy currents, motional EMF and Induced EMF.

Students begin to focus on the torque associated with a current carrying loop in a magnetic field. They solve example problems as a class and use diagrams to visualize the vector product. In addition, students learn to calculate the energy of this loop in the magnetic field.
References
Beaty, William J. High-Ampere Magnetism Demonstration. (electricity science project; 200-amp cable) Last updated May 18, 1998. Science Hobbyist. http://amasci.com/exhibits/hiamp.html
Copyright
© 2013 by Regents of the University of Colorado; original © 2006 Vanderbilt UniversityContributors
Eric AppeltSupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: September 7, 2017







User Comments & Tips