Quick Look
Grade Level: 12 (11-12)
Time Required: 1 hours 45 minutes
(can be split into two 50-minute sessions)
Lesson Dependency:
Subject Areas: Physics
NGSS Performance Expectations:

| HS-PS2-5 |

Summary
Pertinent to their ongoing investigation of MRI machines, students learn the consequences of a charge being subject to electric and magnetic fields at the same time. The lesson covers the Hall effect, velocity selector and the charge to mass ratio. Through several example problems, students calculate the Hall voltage, which is dependent upon plate width, drift velocity and magnetic field strength. Then they calculate the velocity selector, represented by the ratio of the magnitude of the fields, assuming the strength of each field is known. Students perform a series of calculations to arrive at the charge to mass ratio, and finally, a homework problem set, serving as an evaluation of student progress.Engineering Connection
Engineers must understand the combined effects of electric and magnetic fields in order to design safe MRI machines and recognize safety issues. They also apply their understanding of the properties of electric and magnetic fields in applications such as the mass spectrometer. In the provided homework problem set, students use the velocity selector, charge to mass ratio, and the Hall effect to answer questions relevant to the combined effects of electric and magnetic fields.
Learning Objectives
After this lesson, students should be able to:
- Describe the Hall effect.
- Calculate a Hall voltage.
- Use the charge to mass ratio.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS2-5. Plan and conduct an investigation to provide evidence that an electric current can produce a magnetic field and that a changing magnetic field can produce an electric current. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Plan and conduct an investigation individually and collaboratively to produce data to serve as the basis for evidence, and in the design: decide on types, how much, and accuracy of data needed to produce reliable measurements and consider limitations on the precision of the data (e.g., number of trials, cost, risk, time), and refine the design accordingly. Alignment agreement: | Forces at a distance are explained by fields (gravitational, electric, and magnetic) permeating space that can transfer energy through space. Magnets or electric currents cause magnetic fields; electric charges or changing magnetic fields cause electric fields. Alignment agreement: …and "electrical energy" may mean energy stored in a battery or energy transmitted by electric currents.Alignment agreement: | Empirical evidence is required to differentiate between cause and correlation and make claims about specific causes and effects. Alignment agreement: |
International Technology and Engineering Educators Association - Technology
-
Energy can be grouped into major forms: thermal, radiant, electrical, mechanical, chemical, nuclear, and others.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Assess how similarities and differences among scientific, mathematical, engineering, and technological knowledge and skills contributed to the design of a product or system.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
National Science Education Standards - Science
-
Results of scientific inquiry--new knowledge and methods--emerge from different types of investigations and public communication among scientists. In communicating and defending the results of scientific inquiry, arguments must be logical and demonstrate connections between natural phenomena, investigations, and the historical body of scientific knowledge. In addition, the methods and procedures that scientists used to obtain evidence must be clearly reported to enhance opportunities for further investigation.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/van_mri_lesson_4] to print or download.Pre-Req Knowledge
Since this lesson explores the effects of both electric and magnetic fields at once, students should have a basic understanding of electric fields so they can understand how the two relate.
Introduction/Motivation
To solve our MRI challenge, we determined that we need to know how magnetic fields relate to electricity. Because MRI machines include electrical components, we need to learn how the magnetic and electric fields will interact. We need to understand what happens when a charge is subject to both magnetic and electric fields. Engineers need to understand how the electrical and magnetic fields interact in order to understand the limitations set on the individual parts of MRI machines.
How do we determine the properties of electrons that carry currents in a wire? Would any of the laws regarding resistors and capacitors be different if positive particles carried charge?
Lesson Background and Concepts for Teachers
Legacy Cycle Information
This lesson fits into the Research and Rvise phase of the legacy cycle in which students are provided with additional information enabling them to revise their initial ideas for solving the challenge. The research aspect consists of formal lecture on Hall effect, velocity selector, and charge to mass ratio.
Lesson Information
So far, we have looked at what happens to charged particles when a magnetic field is applied, often resulting in a magnetic force, given by the cross product rule. In this section, we look at a few interesting effects that happen when charge is subject to both electric and magnetic fields.
The Hall Effect
In studying electric current without looking at magnetism, note that what sort of particle is carrying the charge through a wire has not been important or even observable. The conventional current is defined as the amount of positive charge moving through a cross sectional area, but it could equally well be negative charge moving in the other direction, and it would not affect the calculated current, power or voltage in any part of any circuit. However, in a magnetic field there can be a difference.
Consider a rectangular piece of thin copper foil laid down on a table and connected to a circuit so that current moves through it from left to right. Assume for a moment that the current really does represent particles with a positive charge, and create a uniform magnetic field pointing down into the foil. If you apply the rule shown below, note that the positive charges are pushed up to one end of the foil, as shown in Figure A.
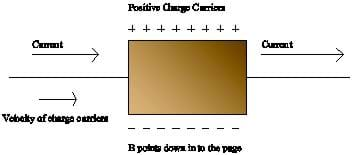
As the positive charges are forced up, charge builds up on the top of the plate, creating a potential difference that one can measure. Assuming that the charge moving through the wire is positive, the upper side will be at a higher potential.
However, what is actually observed in working with metal conductors is the opposite: the upper side is at a lower potential. This can be explained by assuming that the negative charge is actually moving in the opposite direction of the conventional current, which by again applying the same rule (see below) would have negative particles forced up to the top of the plate, as shown in Figure B.
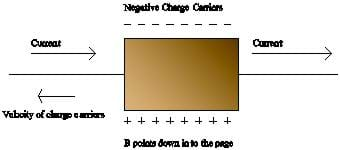
To researchers in the 19th century, this proved that metal conductors contained free charge that was negative.
In this situation, multiple forces are acting on the electrons in the copper plate. As we saw, a magnetic force propels charged particles up to the top of the plate, but as they accumulate on one side of the plate, they generate an electric field pushing them in the other direction. We may assume that this field is uniform and constant in the copper plate, since it is a conductor.
Eventually, so much charge accumulates on the top of the plate that the electric force pushing the electrons down is equal to the magnetic force pushing them up. We call the generated field the hall field, as denoted below. A free body diagram of the electron in the copper plate may be helpful (see Figure C).
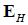
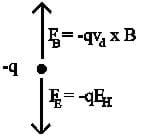
While we cannot measure the field directly, we can measure the potential difference across the plate, which is:
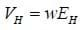
As the particles are in equilibrium, we can write
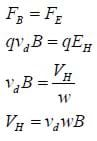
So the Hall voltage depends on the plate width, drift velocity, and magnetic field strength. The drift velocity is difficult to measure directly, but it is related to the current by
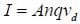
Where n is the number of free charge carriers per unit volume, A is the area of the wire, and q is the charge on each carrier. Now for the copper plate, A=wt where t is the plate thickness. Substituting this and solving for the drift velocity we have
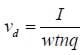
And so the Hall voltage is
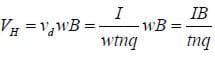
This relationship is extremely useful if we know the properties of a conducting plate; we can measure the voltage across the plate and use this to determine an unknown magnetic field.
Example 1: A rectangle of copper foil with a width of 10 cm and thickness of 0.1 mm is placed in an approximately uniform magnetic field of unknown strength pointing directly through the rectangle. A current of 10 A is run through the rectangle, and a resulting Hall voltage of 325 μV is measured. What is the strength of the field?
Solution: The number of free electrons in copper is 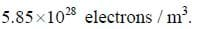
Then
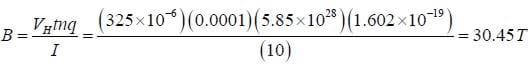
Note that an incredibly strong magnetic field produces a very small Hall voltage in a fairly thin strip of copper with quite a bit of current. This is because copper, as well as other metals, has a large number of free electrons resulting in a very low drift velocity and thus very little magnetic force to be overcome with an electric field.
Example 2: A rectangular strip of germanium with a width of 3 cm thickness of 2 mm is placed in a uniform magnetic field of 2000 Gauss directed straight through the rectangle, and a current of 250 mA is run through the germanium sample. The resulting Hall voltage is .156 mV in the expected direction. What is the number of free electrons per unit volume in the sample, and what is the drift speed of the electrons?
Solution:
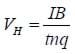
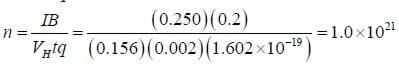
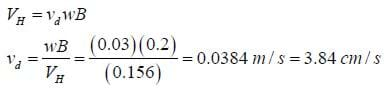
Since germanium has so many fewer free electrons than copper, a small magnetic field can produce a much greater Hall voltage. Since the charge is moving faster for a given current, the magnetic force affects it more. For this reason, a small germanium rectangle is often used as a detection device to determine the strength of a magnetic field. Later on, we will use such a device to measure fields.
The Velocity Selector
When typically slow moving current in a conductor enters into a magnetic field, the result is either that the conductor is pushed to one side if it is free to move, as we saw in a previous activity, or a potential difference is set up across the conductor. However, when a beam of electrons is sent through a magnetic field, it may be deflected as the electrons are free to accelerate as force is applied.
Imagine firing a beam of electrons from left to right through a uniform magnetic field directed into the page. This would deflect the beam down. We could then set up parallel conducting plates above and below the beam (effectively building a parallel plate capacitor) and connect them to a potential difference, thus creating an electric field pointing down. This electric field would produce a force on the beam deflecting the electrons up.
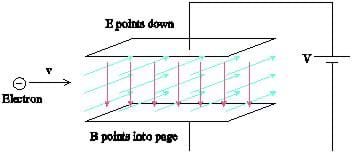
The net force would either be up or down depending on which force is stronger. However, we could change the magnitude of the electric field by either adjusting the potential difference between the plates or changing the plate separation. We could set the strength of the electric field so that the magnetic force and electric force on the electron are the same magnitude, so that no deflection happens. In other words,
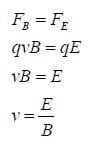
Then, if we know the strength of the fields, we can calculate the velocity of the electrons. The ratio of the magnitude of the fields is thus called the velocity selector.
The velocity selector is used in some types of mass spectrometry. In mass spectrometry, particles are ionized and then accelerated. They come out of the accelerator with different speeds, which makes them hard to analyze. One way to solve this is to send the particles through a velocity selector. Only the particles with a speed of v = E/B get through, while all other particles are deflected. This enables the particles to be analyzed at the same high velocity.
The Charge to Mass Ratio
Near the turn of the 20th century, it was not known what sort of particles carried charge in a conductor, or even if different metals had the same charge carriers. The work of Hall enabled people to separate the current into the drift speed of the charge carriers and the density of the charge carriers, but had not provided information about the carriers beyond the fact that they appeared to be negatively charged in conductors.
At this time, an apparatus had been developed for firing a beam of charged particles through a vacuum off of a conductor with an extremely high voltage. The glass tube containing the vacuum and the stream of particles, called a Crooke's tube, was the early predecessor of the CRT used in many older computer screens and televisions.
At the end of the 19th century, J. J. Thompson used a known uniform magnetic field and a uniform electric field to determine the velocity of these negatively charged particles (now known as electrons) by way of the velocity selector, E divided by B. He would adjust the electric field until no deflection occured and then calculate the fields and hence the velocity of the electrons.
Afterwards, he removed the magnetic field and reapplied an electric field, as shown in Figure E.
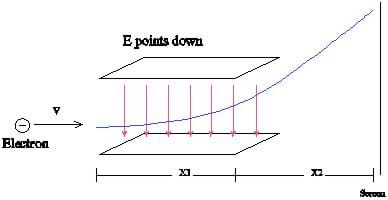
The electron has an initial horizontal velocity 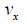
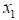
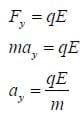
Note that this upward acceleration is proportional to 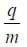
The total time spent between the plates is found using kinematics
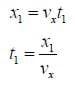
Then the total vertical deflection after it leaves the plates is
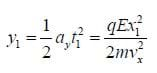
Also, once it leaves the plates it has a vertical velocity
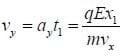
Then as it passes through length 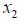
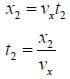
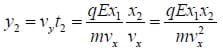
Then the total deflection is
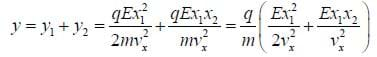
Since the total deflection, the horizontal velocity, the distances and the field can be measured, we can use this equation to calculate 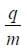
One thing that surprised physicists was that this ratio was the same no matter what metal was used for the cathode, supporting the theory that a single type of particle carried the charge in all conductors. This finding, in combination with Millikan's determination of the fundamental charge of an electron, enabled the calculation of the mass of the electron.
Assessment
Homework Problems: Assign students the Velocity Selector, Charge to Mass Ratio, Hall Effect Homework problem set, which provides an assessment tool enabling teachers to follow students' progress in understanding the concepts.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students induce EMF in a coil of wire using magnetic fields. Students review the cross product with respect to magnetic force and introduce magnetic flux, Faraday's law of Induction, Lenz's law, eddy currents, motional EMF and Induced EMF.

After a demonstration of the deflection of an electron beam, students review their knowledge of the cross-product and the right-hand rule with example problems. Students apply these concepts to understand the magnetic force on a current carrying wire. Through the associated activity, students furthe...

Students are introduced to the effects of magnetic fields in matter addressing permanent magnets, diamagnetism, paramagnetism, ferromagnetism and magnetization.

Students begin to focus on the torque associated with a current carrying loop in a magnetic field. They solve example problems as a class and use diagrams to visualize the vector product. In addition, students learn to calculate the energy of this loop in the magnetic field.
Copyright
© 2013 by Regents of the University of Colorado; original © 2006 Vanderbilt UniversityContributors
Eric AppeltSupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: August 17, 2018








User Comments & Tips