Quick Look
Grade Level: 12 (11-12)
Time Required: 45 minutes
Lesson Dependency:
Subject Areas: Physics

Summary
In this lesson about solenoids, students learn how to calculate the magnetic field along the axis of a solenoid and then complete an activity exploring the magnetic field of a metal slinky. Solenoids form the basis for the magnets of MRIs. Exploring the properties of this solenoid helps students understand the MRI machine.Engineering Connection
Engineers use giant solenoids to create the magnetic fields of MRIs. Just as engineers must understand the properties of solenoids in order to design and build MRI machines, students must understand these properties in order to determine the safety hazards of MRI machines.
Learning Objectives
After the lesson, students should be able to:
- Calculate the magnetic field of a solenoid from its current, radius, and number of coils.
- Explain how a solenoid creates a magnetic field.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
International Technology and Engineering Educators Association - Technology
-
Energy can be grouped into major forms: thermal, radiant, electrical, mechanical, chemical, nuclear, and others.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Assess how similarities and differences among scientific, mathematical, engineering, and technological knowledge and skills contributed to the design of a product or system.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
National Science Education Standards - Science
-
Results of scientific inquiry--new knowledge and methods--emerge from different types of investigations and public communication among scientists. In communicating and defending the results of scientific inquiry, arguments must be logical and demonstrate connections between natural phenomena, investigations, and the historical body of scientific knowledge. In addition, the methods and procedures that scientists used to obtain evidence must be clearly reported to enhance opportunities for further investigation.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Introduction/Motivation
In order to solve the challenge problem, we need to understand the magnetic field of an MRI. The MRI magnet uses a large solenoid to create its magnetic field, so learning the properties of solenoids will help us determine where the magnetic field is present and/or largest.
Engineers study solenoids in order to understand how the "giant solenoid" is going to create a large enough magnetic field for the MRI machine. Engineers continue to test and experiment with more loops and more powerful currents to create larger magnetic fields. Safety engineers make sure these larger magnetic fields do not result in any health or mechanical hazards.
Lesson Background and Concepts for Teachers
Legacy Cycle Information
This lesson fits into the research and revise phase of the legacy cycle during which students are provided with additional information enabling them to revise their initial ideas for solving the challenge. The research aspect consists of a lecture that explains how to calculate the magnetic field along the axis of a solenoid and an associated activity Slinkies as Solenoids exploring the magnetic field of a metal slinky.
The Solenoid
Solenoids in general are also useful to engineers because their magnetic fields can be easily changed by adjusting the current or number of loops. Electromechanical solenoids can be used as switches in pneumatic or hydraulic valves in different engineering projects. After this lesson, during the associated activity, student groups use slinkies (the toy) to discover more about solenoids.
The magnetic field produced by a loop of current is relatively small, due to the size of the constant 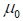
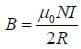
If the wire is coiled several hundred times, many loops may be stacked against each other so that the multiple loops of wire begin to take on the shape of a cylinder. This arrangement is called a solenoid.
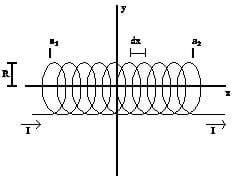
Consider the solenoid shown in Figure A. By the right hand rule, the magnetic field along the x-axis points directly to the right, assuming that the solenoid is tightly wound. To determine the magnitude of the magnetic field at a given point x along the axis, we need to separate the solenoid into clusters of loops with an infinitesimally small length dx. Using the result of the previous homework, if the small segment of loops resided at a point a along the x-axis, the field generated by this group of coils would be:
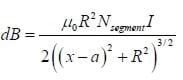
Where 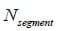
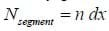
By integration, the total field is:
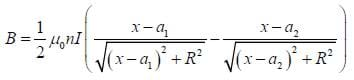
Example:
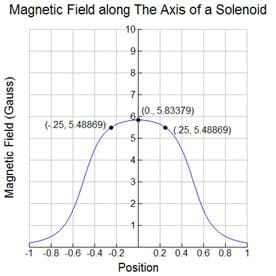
Graph the field along the axis of a tightly would solenoid centered at the origin with a current of 5 A, 100 turns per unit length, a length of 1 meter, and a radius of 20 cm. Use Gauss instead of Tesla for units. (Note: Tightly wound may be taken to mean that n is much greater than I, and we can ignore the current flowing from left to right.)
Solution:
Using these values in the above equation:
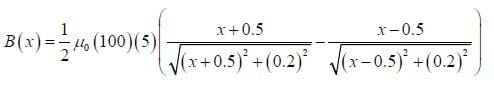
This produces the graph shown in Figure B. The magnetic field produced is close to constant when the position along the x-axis is within the middle half of the length of the solenoid.
If a solenoid is much longer than its radius, and we look at a point near the center of the solenoid, the field can be approximated as:
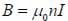
This approximation can be used to a high degree of accuracy when a solenoid has a length at least 10 times its radius and when the point along the axis of the solenoid is closer to the center than it is to the edge.
An Equivalent for Gauss Law?
Unlike electricity, simple examples do not exist to enable us to easily compute a field. For an electric field, a single point of charge enables one to quickly calculate the field using Coulomb's law, but in magnetism, a steady current necessarily involves a continuous curve of current segments, so even the simplest examples require integration. For electrostatic problems involving a high degree of symmetry, the Gauss law enables one to compute the field on a carefully selected surface without integrating. Gauss law states:
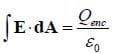
that is the total electric flux, or number of field lines coming out of a closed surface, is equal to the enclosed charge divided by the permittivity of free space. If you recall, electric field lines emerge from positive charges and point into negative charges. However, magnetic field lines never begin or end, but rather form closed loops around segments of steady current. In other words, there is no magnetic charge, and since magnetic field lines never emerge from a point or halt at a point, the total magnetic flux through any closed surface must be zero, that is:
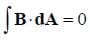
However, this law is not really useful in calculating the magnitude of the magnetic field. It is sometimes called Gauss' law for magnetism or the "no-name law."
Associated Activities
- Slinkies as Solenoids - Students use metal slinkies as solenoids, and test the magnetic field created by sending currents through the slinkies.
Vocabulary/Definitions
solenoid: A current-carrying coil of wire that produces a magnetic field.
Assessment
Embedded Assessment
Assign students the assessment provided in the associated activity, Slinkies as Solenoids. In this activity, students create a lab report in which they design experimental procedures to answer a number of questions that require students to apply what they have learned about solenoids to creating a safe MRI machine.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students induce EMF in a coil of wire using magnetic fields. Students review the cross product with respect to magnetic force and introduce magnetic flux, Faraday's law of Induction, Lenz's law, eddy currents, motional EMF and Induced EMF.

A class demo introduces students to the force between two current carrying loops, comparing the attraction and repulsion between the loops to that between two magnets. After a lecture on Ampere's law (including some sample cases and problems), students begin to use the concepts to calculate the magn...

After a demonstration of the deflection of an electron beam, students review their knowledge of the cross-product and the right-hand rule with example problems. Students apply these concepts to understand the magnetic force on a current carrying wire. Through the associated activity, students furthe...

Students are introduced to the effects of magnetic fields in matter addressing permanent magnets, diamagnetism, paramagnetism, ferromagnetism and magnetization.
Copyright
© 2013 by Regents of the University of Colorado; original © 2006 Vanderbilt UniversityContributors
Eric AppeltSupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: July 1, 2019







User Comments & Tips