Quick Look
Grade Level: 12 (11-12)
Time Required: 1 hours 45 minutes
(can be split into two 50-minute sessions)
Lesson Dependency:
Subject Areas: Physics
NGSS Performance Expectations:

| HS-PS3-5 |
Summary
After a demonstration of the deflection of an electron beam, students review their knowledge of the cross-product and the right-hand rule with example problems. Then they study the magnetic force on a charged particle, compared to the electric force. Provided lecture material covers the motion of a charged particle in a magnetic field with respect to the direction of the field. Finally, students apply these concepts to understand the magnetic force on a current carrying wire. Through the associated activity, students further explore the force on a current carrying wire.Engineering Connection
In their designs, biomedical engineers carefully control the strong magnetic field of MRI machines in order to produce images that do not harm operating personnel or patients. The right-hand rule, commonly used in visualizing the cross product, can be used to study the direction of the magnetic force acting on a charged particle, such as a foreign body entering an MRI's magnetic field. In the Assessment section of this lesson, students use the right-hand rule to predict and test the direction of a magnetic force on a current carrying wire.
Learning Objectives
After this lesson, students should be able to:
- Use the cross product and force equation to determine in which direction a magnetic field acts on a moving particle.
- Describe the motion of a charged particle in a magnetic field.
- Calculate the force of a magnetic field on a current carrying wire.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
HS-PS3-5. Develop and use a model of two objects interacting through electric or magnetic fields to illustrate the forces between objects and the changes in energy of the objects due to the interaction. (Grades 9 - 12) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Develop and use a model based on evidence to illustrate the relationships between systems or between components of a system. Alignment agreement: | When two objects interacting through a field change relative position, the energy stored in the field is changed. Alignment agreement: | Cause and effect relationships can be suggested and predicted for complex natural and human designed systems by examining what is known about smaller scale mechanisms within the system. Alignment agreement: |
Common Core State Standards - Math
-
Solve quadratic equations by inspection (e.g., for x² = 49), taking square roots, completing the square, the quadratic formula and factoring, as appropriate to the initial form of the equation. Recognize when the quadratic formula gives complex solutions and write them as a ± bi for real numbers a and b.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
(+) Recognize vector quantities as having both magnitude and direction. Represent vector quantities by directed line segments, and use appropriate symbols for vectors and their magnitudes (e.g., v, |v|, ||v||, v).
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
(+) Solve problems involving velocity and other quantities that can be represented by vectors.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use units as a way to understand problems and to guide the solution of multi-step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs and data displays.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Compute the magnitude of a scalar multiple cv using ||cv|| = |c|v. Compute the direction of cv knowing that when |c|v ? 0, the direction of cv is either along v (for c > 0) or against v (for c < 0).
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Energy can be grouped into major forms: thermal, radiant, electrical, mechanical, chemical, nuclear, and others.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Assess how similarities and differences among scientific, mathematical, engineering, and technological knowledge and skills contributed to the design of a product or system.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
State Standards
National Science Education Standards - Science
-
Results of scientific inquiry--new knowledge and methods--emerge from different types of investigations and public communication among scientists. In communicating and defending the results of scientific inquiry, arguments must be logical and demonstrate connections between natural phenomena, investigations, and the historical body of scientific knowledge. In addition, the methods and procedures that scientists used to obtain evidence must be clearly reported to enhance opportunities for further investigation.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Worksheets and Attachments
Visit [www.teachengineering.org/lessons/view/van_mri_lesson_2] to print or download.Introduction/Motivation
In order to solve our challenge question, we need to understand how magnetic fields affect physical objects. Since magnetic fields are particularly large in MRI machines, engineers investigate to determine how the human body will react, along with all types of materials that may be associated with the patient. For example, earrings, necklaces and even a metal implant might cause a health hazard that could be fatal. For these same safety concerns, engineers also research which type of materials react to the large magnetic field.
Demonstration: Deflection of an Electron Beam
Objective: The goal of this demonstration is to see how a moving charged particle is affected by a magnetic field. This demonstration is often done with expensive gas discharge tubes. The demonstration described is a low-cost alternative that is safe for students to interact with and has no risk of x-ray exposure. As another alternative, show a video of this demonstration being performed (see https://www.youtube.com/watch?v=0ipm7GikvdQ and https://www.youtube.com/watch?v=3McFA40nP0A).
Materials:
- 1 permanent magnet
- 1 compass
- 1 old CRT computer monitor
- Microsoft PowerPoint® software
To prepare, obtain either a black and white computer monitor, or a color monitor that is due for replacement. Manipulating a color monitor with a magnetic field can damage the display by darkening and/or changing the colors displayed in each pixel. However, old monitors scheduled for replacement are easy to obtain and are often given away for free.
Hook the monitor up to a computer with Microsoft Office® or a similar office software suite. Create a PowerPoint® presentation with a single slide, and set the background of the slide to black. Make a small textbox in the center and set the background of the text box to white. When the presentation is shown, the white box in the center of the screen will be produced by the beam of electrons traveling from the rear of the monitor and hitting the screen in the center.
Use the compass to determine the north pole of the permanent magnet. Place the magnet above the monitor with north pointing down, so as to create a downward-pointing magnetic field. As the electrons are negatively charged, the beam will deflect to the left of the screen, as predicted by the right-hand rule. Have students predict the direction of the beam deflection for a field pointing up, and turn the magnet upside down to produce an upward field. Then place the magnet to the side of the screen so that the beam is deflected up or down.
Warning: This demonstration can damage the way that the monitor displays colors and should only be attempted on a monitor that is has been discarded or is unwanted. Some monitors have a degauss button that can help to remove the residual effects of a strong magnetic field.
Lesson Background and Concepts for Teachers
Legacy Cycle Information
This lesson fits into the Research and Revise phase of the legacy cycle in which students areprovided with additional information enabling them to revise their initial ideas for solving the challenge. The research aspect consists of a demonstration on electron beam deflection, formal lecture on cross products and magnetic forces and the associated activity Force on a Current Carrying Wire exploring the force on a current carrying wire.
Following the lesson, administer the quiz, which serves as part of Test Your Mettle phase of the cycle. This enables teachers to follow students' progress in applying the new concepts.
Lecture Information: Cross Products and the Magnetic Force
Use the following information to guide the class through a review of vector cross-products and an introduction of the Lorentz force. Some example problems are provided along with applications and homework to assign so students become comfortable evaluating the magnitude and direction of the magnetic force on a moving charged particle or a current carrying wire.
Cross Product
First, review the cross product. The cross product, unlike the dot product, is a strictly three-dimensional operation and so is only defined for vectors in 3D space. The magnitude of the cross product between two vectors is given by the equation:
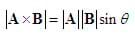
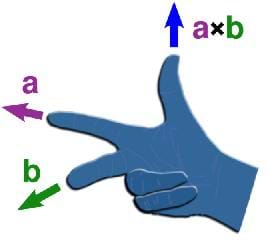
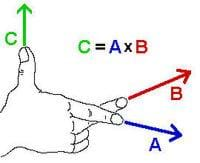
The direction of the cross product is given by the "right-hand rule" as shown in Figure 1. Note that the cross product is perpendicular to both vectors:
The cross product is: 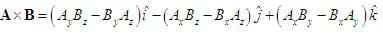
Note the negative in front of the j component.
In most cases, you are given two vectors in a plane and an angle between them, in which case it is sufficient to use the magnitude equation to find the magnitude and the right-hand rule to find which direction the cross product protrudes from the plane.
An example problem:
Find the cross product between the vectors 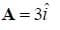
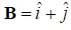
Solution:
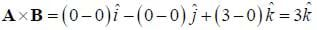
We can also note that A and B both lie in the xy-plane and so the cross product should naturally point along the z-axis. By graphing the two vectors, it is easy to see that the angle between them is 45 degrees, and that 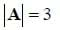
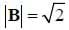

The Magnetic Force on a Charged Particle
Like electric fields, magnetic fields affect charged particles. A magnetic field, which we mapped in the previous activity, has both a magnitude and a direction, and so is denoted by the vector B. The SI unit of the magnetic field is called the Tesla, although this unit is usually inconveniently large. A more convenient unit is the Gauss, where 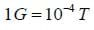
Unlike an electric field, a magnetic field only affects charged particles that are moving, and does not produce a force in the direction of the field. If a particle with charge q is moving with velocity v, the magnetic force on that particle is given by the equation:
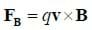
The first thing to note about this equation is that the magnetic force must be perpendicular to both the magnetic field and the direction in which a particle is moving. Note that we can write the magnitude of this force as:
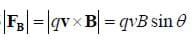
This means that if a charged particle is moving in the same direction as a magnetic field, the angle between the velocity and the field will be zero, and so the particle will not experience a magnetic force at all. On the other hand, if the particle has a velocity perpendicular to the magnetic field, the magnetic force will be at a maximum.
Example:
A particle with mass 35 g and charge 50 μC is moving to the right with velocity 50 m/s in a strong magnetic field of 2.2 T pointing into the board (or page). Calculate the instantaneous acceleration that it will experience.
Solution:
Since the velocity is perpendicular to the field, the magnitude of the force is: 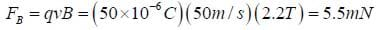
Then the acceleration is 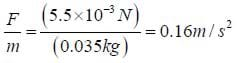
The direction of this force is given by the right-hand rule, and is straight up.
Note that this is not a very large acceleration for a particle moving at 50 m/s. To get a magnetic force of any consequence, it a particle would need to either be moving very fast or have a lot of charge.
Motion of a Charged Particle in a Magnetic Field
The next issue to consider is how a charged particle would move in a uniform magnetic field, assuming that it had some initial velocity v0 and no other forces were acting on the particle.
If the particle is moving along the field, the cross product of the velocity and the field is zero, and so the particle will continue to move in a straight line at a constant speed, with no force acting on the particle (see Figure 2).
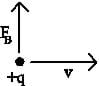
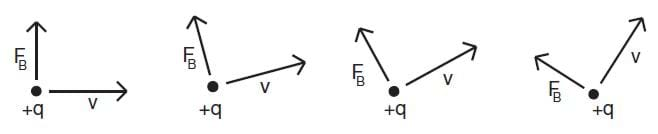
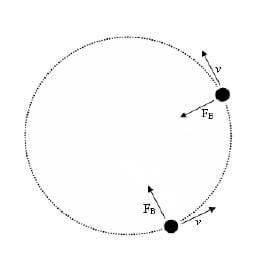
Now consider a particle moving with a speed v in a direction perpendicular to the field. Consider a magnetic field going into the page, and a velocity directed to the right. By the right-hand rule, the magnetic force on the particle would be directed up, as shown.
First, let's determine if this force will change the speed of the particle. In order to do this, consider work and energy. The particle is moving to the right, and makes a 90 degree angle with the magnetic force, so no work is done. The velocity will change direction and gain an upward component, but the speed of the particle will not change.
Once the velocity vector gains an upward component, you might be tempted to say that now the magnetic force is doing work, but when the velocity changes direction, so does the magnetic force, and so by the nature of the cross product, the magnetic force always remains perpendicular to the velocity, thus changing the direction of the motion in the plane, but never changing the kinetic energy of the particle. Over time, the velocity of the particle would change as shown in Figure 3.
Notice that the particle maintains a constant speed and a force that is always perpendicular to the velocity. This is uniform circular motion! We can calculate the radius of the circle using the rule: 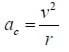
In the most general case, a particle would be traveling neither perpendicular to nor parallel along the field. However, in this case we can split the velocity vector into components perpendicular to and parallel to the field. The perpendicular component would result in circular motion around a field line, while the parallel component would be unaffected. As a result, the particle would spiral around a path parallel to the field. This is called helical motion.
Example:
An electron traveling with an energy of 2 keV is heading directly towards the Earth near the equator, perpendicular to the Earth's magnetic field, which in this area is roughly uniform, directed due north with a strength of 0.005 Gauss. What will the radius, orientation and period of the resulting circular motion be?
Solution:
First convert to SI units:
0.005 Gauss is 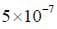
2 keV is 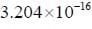
Now find the velocity of the electron in terms of its mass and kinetic energy:
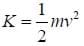
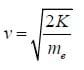
Then, the magnetic force is 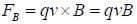
Then, as the electron is undergoing uniform circular motion,
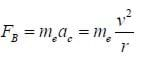
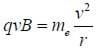
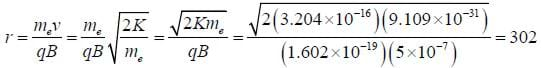
Now for the period,
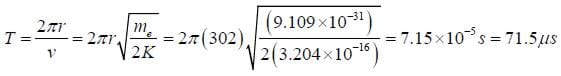
The 302 meter radius circle will be oriented around the magnetic field line, in the plane of the equator, and the period of the particle traveling around the circle will be 71.5 μs.
Magnetic Force on a Current Carrying Wire
The most likely place to encounter moving charge in everyday experience is in a current carrying wire. To determine the magnetic force involved in the wire, we need to know how many charge carriers are moving through it, what the charge on each carrier is, and how fast the charges are moving.
In a normal conducting wire, the charge carriers are electrons, the number of charge carriers per unit volume is the free electron number, and the speed at which they move is the drift velocity. Although the drift velocity is usually extremely slow, there are quite a few charge carriers. Consider a straight wire with length L, area A, free electron number n, and drift velocity vd in a magnetic field B. The force on a single charge carrier would be:
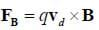
Since there are nAL charge carriers in the wire, the total force on all carriers would be:
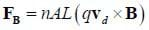
Now the quantity 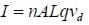
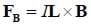
You may note that we changed vd to a scalar and L to a vector. This is acceptable, as long as we retain the direction in some quantity, in this case the length of the wire now refers to both its measured length and the direction of the wire.
For a curved wire, one can think of the wire in terms of small segments that are approximately straight and find the small force on each small segment, in other words
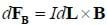
One could then integrate over all the segments to find the total force, which is easier than it seems in situations with certain symmetries.
Example:
Consider an example that could easily be set up in a lab. With a large battery and small resistor, we run a current of 3 A through a wire hung in a nearly horizontal fashion. A small permanent magnet provides a field of about 300 Gauss along about 2 cm of the wire. Hold the magnet so the field is horizontal and perpendicular to the wire. How strong will the resulting force be? How could the direction of the force be reversed without moving the magnet or wire?
Solution:
The magnetic force will be
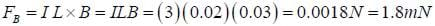
This force will be directed either upwards or downwards. If we hooked the battery terminals in the opposite direction, the current would reverse, and thus the force would reverse direction.
Notice that this force, although small, might produce a visible effect on a light wire. If the force was directed upwards, it could counteract the gravitational force and make the wire appear to float!
Associated Activities
- Force on a Current Carrying Wire - Students run a current through a wire and hold magnets in various positions to establish and explore the magnetic force acting on the wire and how it changes.
Assessment
Homework
Homework Problems: Assign students the Magnetic Force Homework as practice problemsto test their knowledge of magnetic force. Review their answers to gauge their level of comprehension.
Post-Lesson Assessment
Quiz: At lesson end, administer the Magnetic Fields and Forces Quiz to test students' knowledge of magnetic fields and forces, as well as their ability to transfer their knowledge to new situations.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students induce EMF in a coil of wire using magnetic fields. Students review the cross product with respect to magnetic force and introduce magnetic flux, Faraday's law of Induction, Lenz's law, eddy currents, motional EMF and Induced EMF.

Students begin to focus on the torque associated with a current carrying loop in a magnetic field. They solve example problems as a class and use diagrams to visualize the vector product. In addition, students learn to calculate the energy of this loop in the magnetic field.

Pertinent to their ongoing investigation of MRI machines, students learn the consequences of a charge being subject to electric and magnetic fields at the same time. Through several example problems, students calculate the Hall voltage, which is dependent upon plate width, drift velocity and magneti...

Beginning with a class demo, students are prompted to consider how current generates a magnetic field, and the direction of the field that is generated. Via a lecture, students learn Biot-Savart's law (and work some sample problems) in order to calculate, most simply, the magnetic field produced in ...
Copyright
© 2013 by Regents of the University of Colorado; original © 2006 Vanderbilt UniversityContributors
Eric AppeltSupporting Program
VU Bioengineering RET Program, School of Engineering, Vanderbilt UniversityAcknowledgements
The contents of this digital library curriculum were developed under National Science Foundation RET grant nos. 0338092 and 0742871. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
Last modified: June 18, 2019








User Comments & Tips