Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Lesson Dependency:
Subject Areas: Physical Science, Physics
NGSS Performance Expectations:

| MS-PS2-2 |

Summary
The concepts of stability and equilibrium are introduced while students learn how these ideas are related to the concept of center of mass. They gain further understanding when they see, first-hand, how equilibrium is closely related to an object's center of mass. In an associated literacy activity, students learn about motion capture technology, the importance of center of gravity in animation and how use the concept of center of gravity in writing an action scene.Engineering Connection
Engineers are interested in how objects can stay in balance, and what makes them fall out of balance. Mechanical, aerospace and civil engineers incorporate an understanding of equilibrium when they design safe structures. Bridges, cranes, skyscrapers and space stations in stable equilibrium do not collapse, topple to the ground or implode. And, chemical engineers make sure the chemical reactions of the compounds they create remain in equilibrium.
Learning Objectives
After this lesson, students should be able to:
- Describe the concepts of equilibrium and center of mass.
- Relate that an object's center of mass is dependent on the composition and structure of the object.
- Identify how equilibrium and the center of mass apply to engineering and everyday life.
- Identify the various ways equilibrium and the center of mass correlate to different fields of research and scientific disciplines.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-PS2-2. Plan an investigation to provide evidence that the change in an object's motion depends on the sum of the forces on the object and the mass of the object. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This lesson focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Plan an investigation individually and collaboratively, and in the design: identify independent and dependent variables and controls, what tools are needed to do the gathering, how measurements will be recorded, and how many data are needed to support a claim. Alignment agreement: Science knowledge is based upon logical and conceptual connections between evidence and explanations.Alignment agreement: | The motion of an object is determined by the sum of the forces acting on it; if the total force on the object is not zero, its motion will change. The greater the mass of the object, the greater the force needed to achieve the same change in motion. For any given object, a larger force causes a larger change in motion. Alignment agreement: All positions of objects and the directions of forces and motions must be described in an arbitrarily chosen reference frame and arbitrarily chosen units of size. In order to share information with other people, these choices must also be shared.Alignment agreement: | Explanations of stability and change in natural or designed systems can be constructed by examining the changes over time and forces at different scales. Alignment agreement: |
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Attributes of two- and three-dimensional objects are measurable and can be quantified.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Predict and evaluate the movement of an object by examining the forces applied to it
(Grade
8)
More Details
Do you agree with this alignment?
Pre-Req Knowledge
Basic understanding of forces such as lift, weight, thrust and drag.
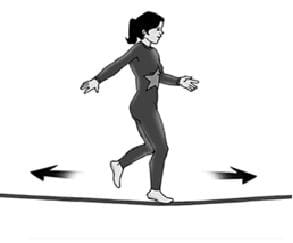
Introduction/Motivation
Have you ever tried to balance on a curb or a tree limb or a bicycle? Was it hard? How did you stay on? People rely upon their sense of balance to keep from falling when they are standing or walking. Another word for balance is equilibrium. Equilibrium is an especially important concept to comprehend (especially for engineers and scientists) because understanding equilibrium is necessary to effectively design structures, such as bridges and buildings. Equilibrium is important for our day-to-day safety. When things are out of balance, or out of equilibrium, they fall over. If they are in unstable equilibrium, they cannot get back into equilibrium after they are out of balance. In other words, if the conditions of stable equilibrium are not met, a bridge could collapse into a river or a building could topple to the ground at the slightest gust of wind! If you ride across a bridge in a car, you do not want to worry about the bridge falling down below your car!
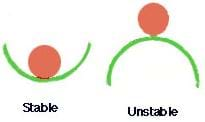
Equilibrium means balance. Stability (as in stable or unstable equilibrium) is the tendency of a system to return to equilibrium after it is disturbed. One way to think of stability is to imagine a ball in a bowl or on a hill (see diagram). If a ball in a bowl is nudged, it will roll back to the bottom of the bowl; a ball in a bowl is in stable equilibrium. On the other hand, a ball balanced on top of a hill will not return to its original position if it is nudged; a ball on a hill is in unstable equilibrium.
Lesson Background and Concepts for Teachers
Engineers are interested in how objects can stay in balance, and what makes them fall out of balance. One way they figure out how to make something balance is to find an average mass point — the spot where there is the same amount of mass in every direction away from that point. Engineers and scientists can do this for any object using some complicated math, but luckily, we can find this "average mass point" easily for certain objects, such as a ruler. All you have to do is to find the right place to put your finger under the ruler so that it will balance. This point of "average mass" is called the center of gravity or the center of mass. What would happen if you hung a small weight on the end of the ruler balanced on your finger? It would begin to tilt towards the weight — it would be out of equilibrium. However, all you would need to do to bring the ruler back into equilibrium would be to move your finger a little bit towards the weight. In other words, you would find that the center of mass moves towards the end of the object that has more mass.
On the surface of the Earth, the terms center of gravity and center of mass are interchangeable. They define the exact same location of an object: the point at the center of the object's mass distribution. However, there are two different names for this "average mass point" because in space, where there is much less gravity, a "center of mass" makes more sense.
Every object has a center of mass. Sometimes, it is easy to guess where the center of mass will be. For example, a pool ball's center of mass is located in the middle of the ball. Usually, if an object is symmetrical, the center of mass is located somewhere on the line of symmetry. However, it is not always easy to guess where on the line of symmetry an object's center of mass is located. For example, imagine a triangle that has two sides with the same length. The triangle can be folded in half and the sides will match up, so there is a line of symmetry, but where on that line is the center of mass? One way to figure it out would be to cut the triangle out of paper, fold it in half along the line of symmetry, and try to balance it on a needle. In this case, you'd find that the center of mass is closer to the wide end of the triangle. This is because there is more mass at the wide base of the triangle than at the pointed top of the triangle; the center of mass is closer to where there is more mass.
For the Tightrope Trials associated activity, students use symmetrical objects to learn about the center of mass. Non-symmetrical objects have a center of mass, too! The center of mass can be found for these objects by examining how they balance, as well. Students examine non-symmetrical objects in the Perching Parrot associated activity.
Engineers are interested in an object's center of mass because the center of mass acts as a point around which forces can be balanced. You can always hold a ruler up with two fingers — one at each end, but if you can find the center of mass, you only need to use one finger to hold the ruler up. The force of gravity pulling down on the ruler can be thought of as lots of little forces along the whole length of the ruler, or as one larger force, acting only upon the center of mass. If an engineer can locate the center of mass, then s/he can figure out where to apply a force to keep that object in equilibrium.
Whenever an object is not moving, or stationary, it is said to be in static equilibrium. As described in Lesson 1, external forces are acting on the object, but they must cancel each other out for the object to be in static equilibrium. For example, a building that is in static equilibrium has two forces — the center of mass pulling downward toward the Earth's center and the ground "pushing up" on the building (Newton's third law). The downward force of gravity and the upward reaction force of the ground must be equal and opposite in magnitude for the building to be in static equilibrium. In terms of analyzing the force of gravity, the building is just like our ruler — we can choose to think of the gravity as lots of little forces acting on every part of the building, or as one larger force acting through the center of gravity.
Like everything else, human bodies have a center of mass. For most adults, the center of mass is located 2 or 3 cm below the belly button, midway between their stomach and back when standing up straight with their arms at their sides. In children, though, the center of mass is a little bit higher (~5%) because typically their heads are larger and their legs are shorter than an adult's. If you stretch your arms straight up, you raise your center of mass by about 5 to 8 cm. Every time you move your limbs, your center of mass moves! Invite the students to think about how their center of mass moves when they walk. Notice that when you stand on one leg, you move your hips over that leg, so that your center of mass is in line with your foot. Without even thinking about it, we adjust our center of mass to stay in equilibrium. Moving our center of mass is what we call balance. If your center of mass gets too far away from your feet, for example when you bend over too far, you are no longer in equilibrium, and you will fall over!
Associated Activities
- Tightrope Trials - To learn about the concept of center of mass, students examine how symmetrical objects balance. Students balance paper cutout "creatures" on a tightrope to explore the ideas of symmetry, balance and equilibrium.
- Perching Parrot - Students examine non-symmetrical objects to find their center of mass. Using a non-symmetrical paper cut-out shape of a parrot sitting on a wire coat hanger, students learn that their parrot exists in stable equilibrium; it returns to its balancing point after being disturbed.
- Exploring Center of Gravity in Motion Caption Technology - Students learn how motion capture (mo-cap) technology enables computer animators to create realistic effects. They learn the importance of center of gravity in animation and to use the concept of center of gravity in writing an action scene.
Lesson Closure
Have the students explain the concepts of equilibrium and the center of mass in their own words. What is the difference between center of gravity and center of mass? (Answer: They are the same for objects on the surface of the Earth, where there is a large enough gravitational field that the gravitational force affecting different objects is uniform. In a location with gravity different than on Earth [like in space], they are not the same because an objects' center of gravity is directly affected by weight.) What are examples of situations in which the consideration of equilibrium is important for engineers? (Possible answer: When they design and build a bridge.) Ask the students to describe how to find the center of mass for various objects.
Vocabulary/Definitions
Center of gravity: The point at the center of an object's weight distribution.
Center of mass: The point at the center of an object's mass distribution. For objects on Earth, this is the same as the object's center of gravity.
Stable equilibrium: A condition in which an object is in balance, and will return to balance if disturbed.
Static equilibrium: A condition in which an object is in balance and not moving.
Symmetry: Exact correspondence of shape on opposite sides of a dividing line or plane through a center or an axis.
Unstable equilibrium: A condition in which an object is in balance, and will not return to balance if disturbed.
Assessment
Pre-Lesson Assessment
Discussion Question: Solicit, integrate and summarize student responses.
- Have you ever tried to balance on a tightrope or a pole? Was it hard? How did you try to stay on? What kept you stable? (Possible answers: Moving your arms and body, crouched or stretched, holding out a pole or stick, all of which are efforts to make adjustments to the location of your center of mass, so you find equilibrium and keep your balance.)
Post-Introduction Assessment
Voting: Ask a true/false question and have students vote by holding thumbs up for true and thumbs down for false. Count the votes and write the totals on the board. Give the right answer.
- True or False: An object that is out of equilibrium will fall over. (Answer: False. The object might fall over, or it might regain equilibrium, depending if it is in stable or unstable equilibrium. Just because you lean one way on a bicycle does not mean that you are going to fall off of it.).
- True or False: Understanding the concept of equilibrium is important for engineers to design and build structures such as buildings and bridges. (Answer: True)
Lesson Summary Assessment
Flashcards: Have the students form into groups of four. Have the students on each team draw different-shaped objects on index cards. On the back of the card have them re-draw the object and mark where the center of mass would be located on it. Have them complete as many as they can in ten minutes. Next, have each student group pair up with another group; have the two teams take turns using their flashcards to test the opposing team on the center of mass locations.
Lesson Extension Activities
Seesaw Fun: With a friend, experiment with balance using a playground seesaw. Sit so that the seesaw goes back and forth evenly. What makes one friend get stuck high in the air? What do you have to do to balance a lightweight child with a heavier friend? Notice that it is not just how much weight is placed on each seesaw arm that determines balance; it is also where that weight is placed. The closer a heavy weight is to the center of the seesaw, the farther from the center the lighter weight must be for the seesaw to be in balance. This seesaw activity also applies to rotational motion because a seesaw also illustrates a type of rotation. The reason for the lighter and heavier weights needing to be placed in different positions is due to torque — the weight of the student times the length of the lever arm.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

The purpose of this lesson is to teach students how a spacecraft gets from the surface of the Earth to Mars. Students first investigate rockets and how they are able to get us into space. Finally, the nature of an orbit is discussed as well as how orbits enable us to get from planet to planet — spec...

To learn about the concept of center of mass, students examine how objects balance. They make symmetrical cut-outs of different "creatures" and experiment with how they balance on a tightrope of string. Students see the concept of center of mass at work as the creatures balance.

Students explore the concepts of center of mass and static equilibrium by seeing how non-symmetrical objects balance. Using a paper cut-out shape of a parrot sitting on a wire coat hanger, they learn that their parrot exists in stable equilibrium — it returns to its balancing point after being distu...
References
Gittewitt, Paul. Conceptual Physics. Menlo Park, CA: Addison-Wesley, 1992.
Hauser, Jill Frank. Gizmos and Gadgets: Creating Science Contraptions that Work (and Knowing Why). Charlotte, VT: Williamson Publishing, 1999. (Source for Seesaw Fun activity.)
Kagan, Spencer. Cooperative Learning. San Juan Capistrano, CA: Kagan Cooperative Learning, 1994. (Flashcards assessment adapted from Kagan.)
Seesaw Physics: FearOfPhysics.com: Kids Playing on a Seesaw, Fear of Physics. January 23, 2004. http://www.fearofphysics.com/Seesaw/seesaw.html
Wolfson, Richard and Jay M. Pasachoff. Physics: For Scientists and Engineers. Reading, MA: Addison-Wesley Longman Inc., 1999.
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Sabre Duren; Ben Heavner; Malinda Schaefer Zarske; Denise CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: December 3, 2020









User Comments & Tips