Quick Look
Grade Level: 8 (7-9)
Time Required: 1 hour
Expendable Cost/Group: US $5.00
Group Size: 3
Activity Dependency: None
Subject Areas: Physical Science, Physics
NGSS Performance Expectations:

| MS-PS2-2 |

Summary
Students learn about two types of friction—static and kinetic—and the equation that governs them. They also measure the coefficient of static friction experimentally.Engineering Connection
Engineers who really understand friction designed a braking system to improve our vehicle safety. Have you been in a car when the driver stopped abruptly by slamming on the brakes, but instead of stopping or skidding, the car started to chatter? That vibration is caused by the anti-lock brake system (ABS). Since engineers know that a non-skidding wheel has more traction than a skidding wheel, they designed a braking system that prevents the brakes from locking up, which can cause a vehicle to slide. By not skidding, the static friction is maximized and the driver can stop the car quickly without loss of control.
Learning Objectives
After this activity, students should be able to:
- Understand how static and kinetic friction are important concepts in engineering design.
- Collect data to solve equations.
- Experimentally measure the coefficient of static friction.
- Recognize that different surfaces have different frictional coefficients.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-PS2-2. Plan an investigation to provide evidence that the change in an object's motion depends on the sum of the forces on the object and the mass of the object. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Plan an investigation individually and collaboratively, and in the design: identify independent and dependent variables and controls, what tools are needed to do the gathering, how measurements will be recorded, and how many data are needed to support a claim. Alignment agreement: Science knowledge is based upon logical and conceptual connections between evidence and explanations.Alignment agreement: | The motion of an object is determined by the sum of the forces acting on it; if the total force on the object is not zero, its motion will change. The greater the mass of the object, the greater the force needed to achieve the same change in motion. For any given object, a larger force causes a larger change in motion. Alignment agreement: All positions of objects and the directions of forces and motions must be described in an arbitrarily chosen reference frame and arbitrarily chosen units of size. In order to share information with other people, these choices must also be shared.Alignment agreement: | Explanations of stability and change in natural or designed systems can be constructed by examining the changes over time and forces at different scales. Alignment agreement: |
Common Core State Standards - Math
-
Summarize numerical data sets in relation to their context, such as by:
(Grade
6)
More Details
Do you agree with this alignment?
-
Reporting the number of observations.
(Grade
6)
More Details
Do you agree with this alignment?
-
Describing the nature of the attribute under investigation, including how it was measured and its units of measurement.
(Grade
6)
More Details
Do you agree with this alignment?
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association.
(Grade
8)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain how knowledge gained from other content areas affects the development of technological products and systems.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Report the number of observations.
(Grade
6)
More Details
Do you agree with this alignment?
-
Summarize numerical data sets in relation to their context.
(Grade
6)
More Details
Do you agree with this alignment?
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities.
(Grade
8)
More Details
Do you agree with this alignment?
Colorado - Science
-
Predict and evaluate the movement of an object by examining the forces applied to it
(Grade
8)
More Details
Do you agree with this alignment?
-
Use mathematical expressions to describe the movement of an object
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- 3 ft fishing line
- small, stiff cardboard box ~5 in x 5 in x 5 in, or a Tupperware container of similar size
- tape (any kind)
- weight scale
- weights (if a problem, see Troubleshooting Tips)
- small basket
- table
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_energy_lesson04_activity1] to print or download.Introduction/Motivation
Friction is not always a bad thing just because it can waste energy, wear down parts and cause things to heat up. Often, friction is a reliable friend. For example, we depend on friction to keep our shoes and chairs from sliding out from under us and keep our cars on the road. When friction is removed from these situations, like when a road is covered with ice, disastrous things can occur.
Two types of friction exist: static friction and kinetic friction. Static friction resists an object to start moving or sliding, which is a good thing when you start walking. If static friction did not exist, it would be like you were constantly walking on ice! Kinetic friction resists an object that is already moving or sliding and always acts in a direction opposite of the motion. Kinetic friction is the reason that anything freely sliding eventually comes to a stop. It is important to note that static friction is always stronger than kinetic friction.
For flat and horizontal surfaces, both static and kinetic friction between an object and the ground can be calculated using the following equation:
FF = μ x W
where FF is the frictional force, μ is the coefficient of friction, and W is the weight of the object. When an object is not sliding, μs is used, which stands for coefficient of static friction. Conversely, μk is used for sliding objects and stands for the coefficient of kinetic friction. Note that μs will always be larger than μk . The values for μ are usually found experimentally. In this activity, a method of measuring μs will be introduced.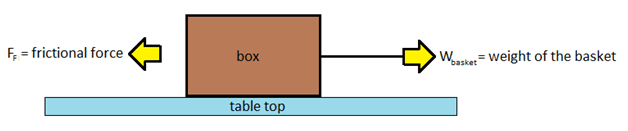
To better illustrate this concept, consider the image above which shows the horizontal forces acting on the box. Because the tension in the fishing line is the same everywhere (assuming the friction between the line and the table is negligible – discussed in the next section), we can assume that the box is being pulled to the right with a force equal to the weight in the basket. The force on the left is the frictional force that resists the force on the right, and is equal to the coefficient of friction multiplied by the weight of the box (in reality, the maximum value of the frictional force is equal to μ x W; if the weight of the basket is less than this maximum value, then these two opposing forces are equal, otherwise the greater frictional force would move the box to the left, which we know is not possible). If the weight of the basket is less than the (maximum) frictional force, then the box will not move. If the weight of the basket is greater than the (maximum) frictional force, the box will move to the right. Mathematically speaking:
- Ff > Wbasket --> box does not move
- Ff < Wbasket --> box moves right
Procedure
Before the Activity
- Collect materials.
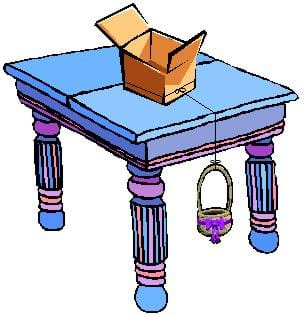
Figure 1. Diagram of the activity setup. The box's friction with the table keeps the basket from falling to the floor. - Make copies of the Sliders Worksheet.
- Designate areas and tables for the students to work.
With the Students
- To get students to think about the activity, brainstorm with them. Ask them to give examples of good (helpful) and bad (potentially disastrous) friction. See the Assessment section for examples.
- Gather materials.
- Record the weight of the box (in grams) in the worksheet table.
- Tie the fishing line around the sides of the box (see Figure 1).
- Position the fishing line on the lower half of the box to prevent the box from tipping over.
- Once in place, tape the line in place so it does not fall off or shift during testing.
- Tie the other end of the line to a basket and hang the basket off the edge of a table (see Figure 1).
- Place 500 grams of weight in the box and gently add weight in the basket, which should be hanging from the line off the side of the table.
- Caution: If the weight is added too quickly or too roughly, it may cause the box to start sliding, and ruin your data.
- Keep gently adding weight until the box starts to slide.
- To increase accuracy, add small amounts of weight (~10g-20g) at a time.
- Weigh the basket and record the weight on the Sliders Worksheet.
- Ask the groups why they think fishing line is being used instead of rope or string. Explain that this is because the fishing line is very thin and smooth, which makes any friction between the table and the line extremely small. So small that it can be ruled out. If we used rope or string, we might have to take into account its frictional effect.
- Repeat for 1000 grams, 1500 grams, and 2000 grams of weight in the box.
- Calculate the coefficient of static friction for each trial.
- μs = weightbasket ÷ weightbox
- In this experiment, FF equals the weight of the basket.
- Average the four values.
- You now have the coefficient of static friction between the table and the box.
- Conclude by conducting the "Pass the Buck" activity from the Assessment post-activity section and asking the discussion question.
Assessment
Pre-Activity Assessment
Brainstorming: In small groups, have students engage in open discussion. Remind students that no idea or suggestion is "silly." All ideas should be respectfully heard. Ask the students to give examples of good and bad friction. (Answers: Good friction = between your sneakers and the ground, or your car tires and the road. Bad friction = in engines, causing them to heat up, wear out and break, or in your skateboard or rollerblade bearings, making it difficult to skate.
Activity Embedded Assessment
Group Questions: During the activity, ask the groups:
- Why are we using fishing line instead of rope or string? (Answer: The fishing line is very thin and smooth, resulting in any friction between the table and the line being extremely small—so small that it can be ruled out. If we used rope or string, we might have to take into account its frictional effects.)
- Which horizontal forces are acting on the box? (Answer: The box is being pulled in one direction by the fishing line – this force is equal to the weight of the basket. The box is being pulled in the opposite direction by the force of friction.)
- What does the force of friction depend upon? (Answer: It depends upon the weight (or mass) of the box and the coefficient of friction.)
Post-Activity Assessment
Pass the Buck: Now that students have measured the coefficient of static friction for a box, have them brainstorm ideas to design an experimental test setup for testing the coefficient for a motorcycle's tires. First, assign one student in the group to be the recorder. Then have someone toss out an idea. Next, another person in the group provides an idea that builds on the first. Go around the group in this fashion until all students have contributed enough ideas to put together a design. When they are done, have them share their ideas with the class. (Example answer: Tie a rope to the motorcycle and see how many people it takes to move the motorcycle. You could test again with a person sitting on the motorcycle and then average the coefficients of friction.)
Discussion Question: Solicit, integrate and summarize student responses.
- What would happen if the kinetic friction of the box was stronger than the static friction? (Answer: If the kinetic friction was stronger, once the box started sliding its friction would increase and stop the box from sliding. Once the box would come to a stop, its friction would decrease again causing an infinite loop of starting and stopping. Now wouldn't that be fun to watch?)
Safety Issues
- Make sure students are not wearing open-toe shoes because dropped weights could injure their feet.
Troubleshooting Tips
If weights are unavailable, use common objects, such as coins, instead, as long as you have a scale to weigh them.
For best results, try to replicate each trial exactly the same. Make sure the box is oriented in the same direction each time.
Activity Extensions
Have students graph their results.
Activity Scaling
- For upper grades, have students plot their results using a computer. Depending on their skill level, have them add a trend-line to their plots and display their equations.
- For lower grades, run through a sample calculation to find μ.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

High school students learn how engineers mathematically design roller coaster paths using the approach that a curved path can be approximated by a sequence of many short inclines. They apply basic calculus and the work-energy theorem for non-conservative forces to quantify the friction along a curve...

In this hands-on activity, students learn about two types of friction — static and kinetic — and the equation that governs them. They also measure the coefficient of static friction and the coefficient of kinetic friction experimentally.

Students learn about friction and drag — two different forces that convert energy of motion to heat. Both forces can act on a moving object and decrease its velocity. Students learn examples of friction and drag, and suggest ways to reduce the impact of these forces.

Learn the basics of the analysis of forces engineers perform at the truss joints to calculate the strength of a truss bridge known as the “method of joints.” Find the tensions and compressions to solve systems of linear equations where the size depends on the number of elements and nodes in the trus...
Copyright
© 2004 by Regents of the University of Colorado.Contributors
Chris Yakacki; Malinda Schaefer Zarske; Denise W. CarlsonSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: April 13, 2019









User Comments & Tips