Hands-on Activity Volume & Data:
Build the Biggest Box Using One Piece of Paper

Learning Objectives

After this activity, students should be able to:

• Explain how to create the biggest box.
• Improve on their first designs and create better second boxes.
• Discuss how volume is used in engineering.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

Each group needs:

• 2 sheets of construction paper, 8.5 x 11-inches or larger; must be the same size paper for all groups
• scissors
• scotch or masking tape
• ruler

The instructor needs:

• puffed rice, an amount that is sufficient to fill the largest possible box students create from the provided one sheet of paper; such as a bag of puffed rice cereal for ~$3
• measuring cup, for the puffed rice
• chalk or white board markers, to record volumes on the classroom board
• tape (or magnets) to attach paper boxes to the classroom board

Introduction/Motivation

What does it mean for something to be “big”? We think about size in lots of different ways. Sometimes we think about large things as being extremely tall, such as skyscrapers, or very long, such as huge suspension bridges. Often we say that things are “big” when they can hold a lot of “stuff,” such as an Olympic-sized swimming pool or a sports stadium.

Today we’re going to talk about what makes something “big,” and we will do so in the form of an engineering challenge—to create the biggest possible box from a sheet of construction paper. The definition of “big” that we’ll use for this challenge is how much can it hold. In the engineering world, we refer to this as volume.

Volume is a useful tool for engineers in any discipline. Civil, environmental and architectural engineers might consider the volume of people that need to occupy a new office building they are designing, or water that is contained in a new reservoir design. Chemical engineers might need to consider the volume of a material in developing a new pharmaceutical pill. Aerospace engineers think about volume when they design fuel tanks for airplanes and space shuttles. Today, you will learn what volume is and how to increase and decrease the volume of an object. (Continue on to conduct the activity, as described in the Procedure section.)

Procedure

Activity Overview

Student pairs are each given one piece of construction paper and challenged to use the paper to make the biggest box possible (largest volume). The box does not need to have a top, and the paper may be cut any way they choose. After a team has completed its box, the instructor measures how much puffed rice the box can hold. Students write on the classroom board how much rice it held and then tape the box on the board near its volume. Then the group is given a new piece of paper and attempts to construct a bigger box. Using the volume equation, they also calculate the box volumes. Then they plot and analyze the class data for the measured and calculated box volumes.

With the Students

1. Present to the class the Introduction/Motivation content.
2. Give students more detail about volume:

• Say: Volume is the amount of space that an object occupies, or the amount of space enclosed inside an object. For a coffee cup, we might say that its volume is the amount of coffee that the cup holds. For a brick, its volume is the amount of space that it takes up.
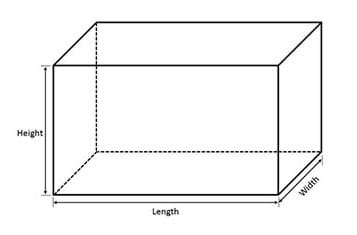
• Say: Today, we’ll be constructing empty boxes using construction paper. Each box will have five rectangular sides and no top. We call this shape a rectangular prism, which is simply a three-dimensional projection of a rectangle. We can compute the volume of a rectangular prism using the following equation: length x width x height (draw Figure 1 on the classroom board). You may want to utilize this equation to come up with a design for your box that maximizes its volume.

3. Continue the discussion by talking about how to measure volume:

• Ask students to suggest some different ways in which they might measure to determine which box is biggest. Say: How will we know which box is biggest—has the biggest volume? How can we measure it? If student suggestions involve using the volume equation, tell them to think on a simpler, more intuitive level for now. Guide students to eventually agree on determining the biggest box based on how much the box holds.
• Say: I have a supply of puffed rice, so for this activity, we’ll consider the amount of puffed rice held by the box as a surrogate for the actual volume of the box, for comparison purposes.
• Then, as a class, agree on a procedure for how all the boxes will be measured for volume. For example, fill the box with puffed rice, shake it to make sure no more puffed rice can fit, but level it off to make sure no puffed rice are above the top edge of the box.
• (optional) Record the measurement “rules” on the board to help students remember.

4. Divide the class into groups of two students each (or no more than three per group).
5. Provide each group with one piece of construction paper, tape, scissors and a ruler.
6. Clarify the engineering challenge: Work together as a group to construct the largest possible box. The box must have four sides and a bottom, but no top side. You may cut the paper any way you want. Tape may only be used to hold sides together and not be used to add any area to the box. (optional) Record the challenge constraints on the board to help students remember.
7. Give teams 10-15 minutes to construct their boxes.
8. Halt all construction to measure the box volumes: Fill a box to the top with puffed rice and then transfer that rice into a measuring cup to determine the volume. Have students record the volumes for each group’s box on the board next to the group name; use tape (or a magnet) to attach the box next to its volume.
9. (optional) Ask students to rank/organize the results list in order from smallest to largest volume. This guides students to take note of the first iteration results across the class.
10. Lead a class discussion about how teams might improve their designs, as described in the Assessment section.
11. Provide each group with a new sheet of construction paper, and direct the teams to each design a second box, applying the lessons learned from the design of the first box. The goal is to design a box that holds more puffed rice than the first box.
12. After 10-15 minutes, halt group construction work and measure the second box design volumes using the same measurement procedure as before.
13. On the board, alongside the previous boxes and volumes, have students record the new volumes. Take note of groups that improved upon their designs.
14. (optional) Have students use rulers to measure the box dimensions and then calculate the box volumes in in³ or cm³.
15. Conclude with a class discussion and data analysis assignment, as detailed in the Assessment section.

Vocabulary/Definitions

maximize: To make as large or great as possible.

rectangular prism: A three-dimensional, solid object that has six faces that are each rectangles.

volume: The amount of three-dimensional space that a substance or object occupies or contains.

Assessment

Pre-Activity Assessment

Question: Ask students: How can the concept and understanding of volume be used to solve problems in the real-world? Have students brainstorm a few ideas and discuss as a class. (Possible answers: For following recipes, space planning and space optimization, ordering the right amount of concrete to pour a section of sidewalk, planning the capacity of storm drains and water reservoirs, water flow and water treatment, military use, manufacturing, structural engineering.)

Activity Embedded Assessment

Between Iterations Discussion: Between box-making iterations, ask students: How would you improve your box? Before beginning their second designs, make sure students take some time to recognize issues with their original designs and make plans to improve them to hold more volume.

Post-Activity Assessment

Concluding Discussion: Lead a class discussion to gauge the overall success of the activity. Ask students:

• Were you able to make a box and then improve your box design? What worked well? What did not? Engineers often work through the design of a product just as you did today. They design and build something, test it out or compare it with the original idea, see what doesn’t work and how it measures up to the objectives, and then make improvements to make it better.
• What would you do next time to make your box even better? (Possible answers: Use different materials, improve the amount of time to make the box [efficiency], use different adhesives to hold the box sides together.)
• What is volume? What is the equation for volume of a box—a rectangular prism? What are some examples of volume from our daily lives? (Possible answers: Volume measurements on beverage and food labels, vehicle fuel tanks, swimming pools, food recipes, packing a suitcase or truck, etc.)
• Why is volume important to engineers? How does it impact design? What types of engineering projects might focus on volume? (Possible examples: Water reservoirs and dams, building designs, fuel tanks for vehicles—especially planes and rockets.)
• How is iteration important to the design process? (Point to make: Teams learned from their first designs and were able to make adjustments in order to increase the box volume. Engineers use the same process to improve product performance and optimize design solutions. What might be called failure [early design attempts] often leads to further iteration [revised designs] that result in improvements and better final design solutions; so iteration is an important part of the design cycle.)

Data Calculation and Analysis: Assign students to create a class data table that includes the measured volumes of puffed rice held by each box and the calculated volumes of each box. Then plot these values against each other for each box to generate a relationship between the two. This exercise has students compare the theoretical (calculated) to the actual (measured) volumes. Hypothetically, they should be the same, as evidenced by a linear relationship on their graphs. However, human error in the measuring process is likely to yield some variation.

Activity Scaling

• For lower grades, eliminate the use of volumetric equations. Discuss volume in more qualitative ways and do not calculate the box volumes.
• For higher grades, conduct the activity by having students create more complex three-dimensional shapes such as cylinders and pyramids, which have more complicated volume equations.

References

Copyright

Contributors

Supporting Program

Acknowledgements

This activity was developed by CU Teach Engineering, a pathway to STEM licensure through the Engineering Plus degree program in the College of Engineering and Applied Science at the University of Colorado Boulder.