Quick Look
Grade Level: 9 (8-10)
Time Required: 5 hours 45 minutes
(170 minutes in class and ~180 minutes outside of class; entire project spread over 3-4 weeks)
Expendable Cost/Group: US $0.00 This activity also requires each student to provide materials from home with which to make a scale model of a chosen object from home.
Group Size: 1
Activity Dependency:
Subject Areas: Geometry, Measurement
Summary
Students build scale models of objects of their choice. In class they measure the original object and pick a scale, deciding either to scale it up or scale it down. Then they create the models at home. Students give two presentations along the way, one after their calculations are done, and another after the models are completed. They learn how engineers use scale models in their designs of structures, products and systems. Two student worksheets as well as rubrics for project and presentation expectations and grading are provided.
Engineering Connection
Engineers use scale models in many different aspects of their work. Architectural engineers fabricate scale models of the buildings they are designing to see how sunlight affects the space or to show to clients. Engineers often use scale models when prototyping projects that would otherwise be too large or costly to test for functionality. Often, the results of testing done on scale models can be applied to full-size models, making it more economical to begin large engineering projects with scale model testing. Scale models are commonly used in wind tunnels for airfoil designs that are later scaled up for full-size aircraft.

Learning Objectives
After this activity, students should be able to:
- Explain how scale models are used in real life.
- Create an accurate scale model using the mathematical tools provided in the associated lesson.
- Describe how engineers use scale models in the design of products, structures and systems.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
Common Core State Standards - Math
-
Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Identify the shapes of two-dimensional cross-sections of three-dimensional objects, and identify three-dimensional objects generated by rotations of two-dimensional objects.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Visualize relationships between two-dimensional and three-dimensional objects
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Apply geometric concepts in modeling situations
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use geometric shapes, their measures, and their properties to describe objects (e.g., modeling a tree trunk or a human torso as a cylinder).
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the role of troubleshooting, research and development, invention and innovation, and experimentation in problem solving.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Attributes of two- and three-dimensional objects are measurable and can be quantified.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Visualize relationships between two-dimensional and three-dimensional objects.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Apply geometric concepts in modeling situations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use geometric shapes, their measures, and their properties to describe objects.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Identify the shapes of two-dimensional cross-sections of three-dimensional objects, and identify three-dimensional objects generated by rotations of two-dimensional objects.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
Each student needs:
- rulers
- graph paper
- pencils
- an object of his/her choice, to create a scale model of; this is open-ended; might be brought from home or found in the classroom; might be simple like books, erasers and sticky note pads, or more complex like canned/boxed food items and sports equipment
- scale model building materials, for students to acquire and use at home; this is open-ended; consider providing some basic materials and tools such as cardboard, cardstock, construction paper, foam core board, markers, paint, toothpicks, contact paper, foam, papier-mâché, tape, hot glue, depending on the original objects
- Project Overview and Rubrics
- Choosing a Scale Worksheet
- Area and Volume Worksheet
To share with the entire class:
- yardsticks
- tape measures
- Engineering Drawing Examples, a few printouts to show the class
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_scale_model_lesson01_activity2] to print or download.Pre-Req Knowledge
- An understanding of the relationship between side length, area and volume, as well as a general, non-calculated (intuitive) sense of volume, which is covered in the associated lesson, Discovering Relationships between Side Length and Area, and activity, Build the Biggest Box.
- Completion of the associated lesson, Discovering Relationships between Side Length and Area.
- Ability to calculate surface area and volume of rectangular prisms, cylinders and spheres.
- Familiarity with using rulers and other measuring tools.
Introduction/Motivation
We have spent the past few days looking at the relationships between dimensions of shapes and their areas and volumes. Now we are going to take this knowledge and apply it to build scale models.
In the real world, scale models are used by engineers for many different purposes. When engineers are prototyping projects, they often fabricate scale models to see if their plans function as intended. Engineers also use scale models to understand how something works. Architectural engineers often create scale models of their buildings to see how the sun’s orientation affects the various rooms or to make other observations about their building’s spaces. Airplane and wing designs are typically tested at reduced scale in wind tunnels in order to determine if they function as intended. (Show students Figure 1, a scale model test of a passenger aircraft in a wind tunnel.)
The results of these scale model tests can be applied to full-scale models, helping engineers to make sure their designs work before they are even built. For example, when the Golden Gate Bridge was built in the 1930s, the engineers verified their suspension bridge design theory calculations with tests on a steel tower model that was 56 times smaller than one of the full-size bridge towers, confirming before construction began that the tower calculations were sound.

In this project, you will get to work like engineers and create scale models of objects of your choosing. Look for an object with relatively simple geometry—or one with geometry that has the potential to be simplified easily. You will decide which dimensions are going to help you construct an accurate scale model. In addition, you will need to explain how scaling the object affected the area of the base and the volume of the object, based on our work these past few days. You will use the patterns we discovered about circles, squares, rectangular prisms and cylinders to build a scaled down (or scaled up) version of your object. Throughout the process, you will also create engineering drawings and practice your presentation skills. (Continue on to present to students the content provided in the Procedure > Background section.)
Procedure
Background
Developing scale models involves taking full-scale objects or designs and (most commonly) reducing all of their dimensions by a common factor. Figure 2 illustrates this concept with a simple rectangle. Models are also sometimes “scaled up” by increasing all the dimensions by a common factor.
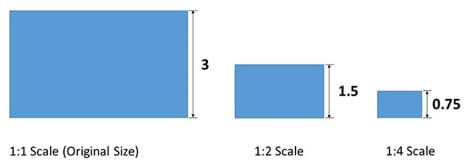
Looking at Figure 2, we can see that the rectangle on the left side is 1:1 scale, which is a full-scale model. The middle rectangle is 1:2 scale, meaning that the original dimensions of the rectangle (length and width) have each been divided by 2, and are now half as long. Similarly, the far right rectangle (1:4 scale) possesses the original dimensions divided by 4. Notice that the areas of the rectangles do not scale by the same factor. This is because the area is a squared term, meaning that changes to the length and width do not affect the area linearly; this is illustrated in Figure 3.
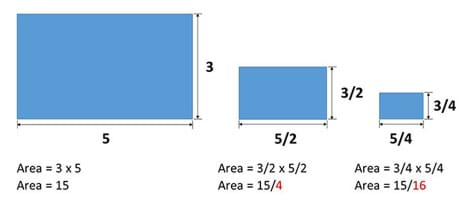
Looking at Figure 3, we can see why area does not scale linearly. The scaling factor in the denominator becomes squared, causing the area to decline more rapidly than the individual side lengths. The area of the 1:2 scale rectangle is one-quarter of the original area, while the area of the 1:4 scale rectangle is one-sixteenth of the original area.
When creating a scale model, one approach is to pick an appropriate scaling factor and simply apply it to all dimensions. Alternatively, if a specific dimension is desired for the physical scale model, one can obtain the scaling factor by dividing the original dimension by the desired scale dimension. Then this factor can be applied to all other original dimensions to produce the scale model dimensions.
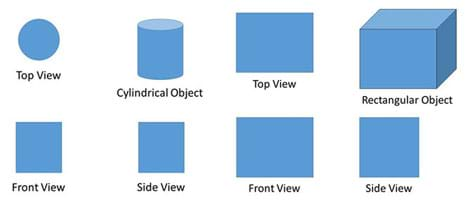
Figure 4 shows examples of engineering drawings for cylinders and rectangular prisms. While the views used in engineering drawings may be chosen somewhat arbitrarily, once one view is selected, the others MUST be relative to that view. Each view is 90 degrees relative to each of the other views. The front view often includes prominent features of the object, while the top view is how the object appears from directly overhead.
(Note: Additional background information about area, volume and dimensions can be found in the associated lesson and activity.)
Before the Activity
- Gather materials.
- Adjust and personalize the project timeline listed in the Project Overview and Rubric to reflect your in-class schedule, specific dates, and how much time you give students to work on their scale models at home.
- Make copies of the Project Overview and Rubrics, Choosing a Scale Worksheet and Area and Volume Worksheet.
- Make a few copies of the Engineering Drawing Example to pass around the class. FYI, a reduced-size version of the drawing example is included in the Choosing a Scale Worksheet.
Day 1: Project Introduction and Overview (20 minutes)
- Present to the class the Introduction/Motivation content as well as the mathematical background information.
- As a class, go over the project overview and rubrics handout. Explain your expectations for the interim milestones and final project. Make clear everything you want handed in as well as due dates.
- Ask students to pick an object from home for which they want to create a scale model and bring it with them to class the following day. Explain that they will start working on the project in class and it is absolutely necessary for them to have the objects in hand.
Day 2: Project Work Day—Choosing a Scale (50 minutes)
With their objects in hand, direct students to refer to the Choosing a Scale Worksheet to guide them through the following procedure.
- Students measure and record all object dimensions that they think they need in order to create scale models.
- Based on these dimensions, students pick an appropriate scaling factor. As necessary, help them pick a reasonable scale based on feasibility and time.
- Students create engineering drawings of their objects, making sure to include on the drawing the important dimensions they measured. As examples, show students the Engineering Drawing Example (which is also reproduced on the worksheet, in reduced size) and Figure 4.
- See the Investigating Questions section for question prompts to help guide your discussions with students about choosing a scale. At class end, make sure students know when the next deliverable is due and explain that the remainder of this project will be done at home. Hand out the Area and Volume Worksheet to be completed at home.
Day 3: Presentation 1 (50 minutes)
- After students have had one or two weeks to work on the project, have them present their work thus far. Refer to the Project Overview and Rubrics for more details.
- Make sure students include descriptions of their struggles and successes in their work so far.
- Expect each student to have one completed engineering drawing of his/her object. Depending on presentation length and number of students, this may take more than one day.
- Give students feedback to help them continue their work on the project. Remind them of the next due date.
- See the Investigating Questions section for question prompts to help guide your discussions with them about the engineering drawings and presentations.
Day 4: Final Scale Model Due and Presentation (50 minutes)
- A few weeks later, students bring in their final scale models and present them to the rest of the class.
- Expect students to have two different completed scale engineering drawings of the object—from different perspectives—and both worksheets ready to turn in.
- Students share their work with the class and explain what was challenging about their projects.
- Students share the mathematical logic and calculations they completed in order to create the scale models.
- After all students have presented, lead a class discussion to make some real-world connections. Ask the students:
- How does this project, which is about scale models, also model real-world engineering? (Possible answers: Modeling is often part of the design process in the creation of products, structures and systems. Architectural engineers model buildings. Civil and environmental engineers model city planning, transportation and water systems. Mechanical engineers model prosthetic limbs and manufacturing automation systems.)
- Of all these examples, which ones might be easy to model and which ones might be more difficult to model? (Possible answers: Modeling of buildings is extremely useful to see what the spaces will look like and make sure mechanical components are not in conflicting places. However, this might be easier to model on a computer rather than building precisely detailed physical models. On the other hand, in addition to making computer models of prosthetic limbs, it would be helpful to make and experiment with physical models of prosthetic limbs because engineers can see how the devices behave and get human user feedback.)
Vocabulary/Definitions
model: (noun) A representation of something for imitation, comparison or analysis, sometimes on a different scale. (verb) To simulate, make or construct something to help visualize or learn about something else (as a product, process or system) that is difficult to directly observe or experiment upon.
prototype: A first attempt or early model of a new product or creation, from which later versions are developed.
scale: The relationship, or proportional ratio, of a linear dimension of some feature of a model, map or drawing of an object to the same feature of the original object.
Assessment
Pre-Activity Assessment
Initial Measurements: Students measure all the linear dimensions on their objects that they believe will be necessary to make the models. This indicates to the teacher whether or not students understand the key dimensions and the relationships between these dimensions and area/volume.
Activity Embedded Assessment
Presentation 1: Now, halfway through the process, students give presentations. This indicates to the teacher how much progress students have made and is a good time to provide helpful tips.
Post-Activity Assessment
Final Presentation: Students present all of the work they have done in order to create scale models. Refer to the Project Overview and Rubrics for grading.
Final Deliverables: Students turn in their scale models, engineering drawings and calculations for teacher review. Refer to the Project Overview and Rubrics for grading.
Investigating Questions
Choosing a Scale:
- With this scale, approximately how big will your model be?
- Will you be able to build this in the time given, or is it too big?
- Will your model be easy to transport?
- Do you think you can get the materials necessary to create this model—or should you consider choosing a smaller scale?
Engineering Drawings:
- How big is the piece of paper? How many boxes (graph paper grids) each way?
- What are some possible scales you might use and about how much of the paper will they take up?
- How do you know you cannot fit a bigger scale on the paper?
Presentation 1:
- Does anyone have any ideas about how to help <student name> with the aspect s/he is currently finding challenging?
Troubleshooting Tips
Be aware that it can be very difficult to create scale models of cylinders and spheres since it can be challenging to find materials that are the right size.
Activity Scaling
- For lower grades, use very simple objects (blocks). Perform several simple engineering drawings on graph paper, translating one unit to one inch or cm, etc.
- For older students who have CAD experience, have students prepare CAD models of their objects.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!Copyright
© 2016 by Regents of the University of ColoradoContributors
Andi Vicksman; Malinda Zarske; Russell Anderson; Ryan Sullivan; Nathan Coyle; Maia Vadeen; Aaron LamplughSupporting Program
CU Teach Engineering (a STEM licensure pathway), Engineering Plus Degree Program, University of Colorado BoulderAcknowledgements
This activity was developed by CU Teach Engineering, a pathway to STEM licensure through the Engineering Plus degree program in the College of Engineering and Applied Science at the University of Colorado Boulder.
Last modified: October 13, 2018





User Comments & Tips