Lesson Discovering Relationships between Side Length and Area

Learning Objectives

After this lesson, students should be able to:

• State the relationship between the side length and area of a square.
• State the relationship between the radius and area of a circle.
• Describe examples of how area, perimeter and circumference are used in engineering.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Worksheets and Attachments

Pre-Req Knowledge

• How to calculate the area and perimeter of a square.
• How to calculate the area of a circle.
• The circumference of a circle is 2πr.
• How to solve for the radius of a circle given its circumference.

Introduction/Motivation

(In advance, make copies of the Corral Fencing Worksheet, one per student.)

Today we are going to work on finding some patterns for squares and circles. The patterns that we discover today will be very helpful to us in our final project. Why is it important to be able to discover and know the patterns between the dimensions and areas of geometric objects? Well it is important to engineers. They need to understand patterns like the ones we will explore today to help them design and build almost everything, including building structures, products, factory assembly lines and rockets.

(Hand out the worksheets. Divide the class into groups of three or four students each.)

Work within your groups to complete this worksheet. You have 30 minutes. After that, we will discuss the worksheet problems as a class, and some of you will share your work on the board.

(On the worksheet, students are presented with a ranching scenario and asked to calculate the areas that would result from building square horse corrals with 300, 600 and then 900 feet of fencing. Students make in-out tables to assist them in noticing patterns and generalizing the mathematical relationships. Expect students to discover that area increases proportionally to the square of how much the side length increases.)

(Circulate and help students as needed. Before answering any student questions, make sure that they cannot be answered by any other member of the group. This ensures that students work together and ask each other for help. After 25 minutes, have groups share their solutions with the rest of the class, either verbally or on the classroom board. Then go over the problems as a class. Refer to the Assessment section for discussion prompts and a follow-up problem for the class.)

Today, we solved problems that would be helpful in designing horse corrals for a ranch, and in a similar way, engineers apply their understanding of areas and volume when they design products. For example, a container that maximizes volume and minimizes surface area reduces manufacturing materials costs and can increase production efficiency. Understanding the relationship between length and area helps us in many ways—such as to furnish a classroom to hold the right number of desks or tables, or to create blueprints for new buildings.

What are some other examples in which the corral problem could be used in engineering? (Possible answers: To survey property lines, to fence an area of land, to construct roads and parking lots, to design a building or a swimming pool, etc). Using the associated activities, Volume & Data: Build the Biggest Box Using One Piece of Paper and Math Relationships: Scale Model Building Project, students can investigate real world examples with hands-on investigations. 

Lesson Background and Concepts for Teachers

The area of a shape is simply the squared dimension inside of the perimeter of the shape. We regularly use area when we talk about the “square footage” of property or space. This value is simply the area of the floor space in square feet or ft². Figure 1 shows a graphical representation of this concept using square units to represent a rectangular shape.

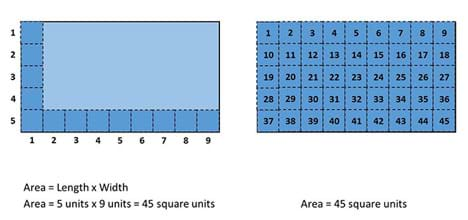
Looking at the left rectangle in Figure 1, we see the rectangular shape is exactly 5 units long by 9 units wide. If we apply the equation for the area of a rectangle, we find that the area of this rectangle should be 45 square units. The right rectangle in Figure 1 has been completely filled in by square units, so we can clearly see that exactly 45 square units fit within the rectangle. This illustrates the concept of area, and demonstrates how area formulae can be applied to quickly determine the area within a given shape.

Different area formulae must be used for shapes of different geometries. Rectangles, triangles and circles all have unique equations to calculate their areas. Figure 2 shows the equations to calculate the areas of circles and rectangles.

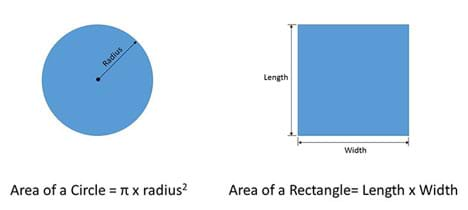
One can see that the more complex geometry of the circle results in a more complex area equation. This formula contains both a squared term for the radius and the mathematical constant pi (π).

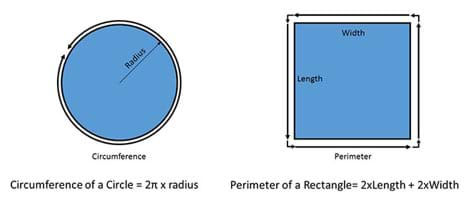
A circle’s radius is also related to its circumference, which is the distance around the circle. Figure 3 illustrates this relationship, and provides the equations for calculating the circumference from a circle’s radius.

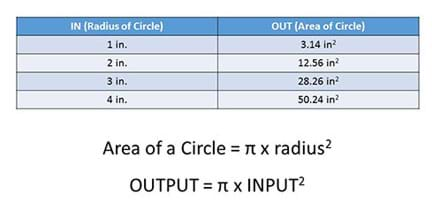
Using an in-out table can help students to “see” the mathematical relationships. For example, as shown in the table in Figure 4, the values in the in column undergo a specific process to obtain the value that goes in the out column. In this case, that involves inserting the in column value (radius of a circle) into the area equation to obtain the out column value (area of a circle).

Associated Activities

• Volume & Data: Build the Biggest Box Using One Piece of Paper - Students learn how engineers use dimensions in their design work, and are challenged to create the biggest box possible in 10 minutes using just one piece of construction paper. Each student measures his/her box volume, then iterates to improve the design to create a bigger box. Students plot and compare collected and calculated volume data, looking for patterns.

  Watch this activity on YouTube

• Math Relationships: Scale Model Building Project - Students learn how engineers use scale models in their design work, and create scale models of objects of their choice. In class they measure their objects and decide on scales. Then they build their scale models at home, completing worksheets, making calculations and giving two short presentations.

  Watch this activity on YouTube

Lesson Closure

Today, we learned that an understanding of the concepts of area and volume are important to the efficient design of many kinds of products and structures. We also observed how an object’s dimensions are related to its area, and saw this pattern by using an in-out table. Engineers often use these same problem-solving methods when determining property lines, drawing street layouts, and performing other city planning tasks. We are going to continue to learn about how engineers use geometry in design when we work on our scale model projects!

Vocabulary/Definitions

area: A quantity that expresses the extent of a two-dimensional figure or shape.

circumference: The linear distance (or path) around the edge of a circle.

perimeter: The linear distance (or path) around a two-dimensional shape. The measurement of the distance around the outer edge of a shape or area.

radius: A straight line from the center to the circumference of a circle or sphere.

Assessment

Pre-Lesson Assessment

Questions: Before starting the lesson, lead a class discussion to gauge student understanding of the concepts of area and patterns, as well as some real-world examples. Ask the students:

• What is “area”?
• How is it used in the real world? (Possible answers: A way to describe the size of buildings and land, such as square footage, buying carpet, how much paint to buy, making sure a sofa fits in your living room, city planning, etc.)
• What are some engineering applications in which knowing area, circumference or perimeter are important to solve problems? (Possible answer: Designing highways or parking lots that are sized to work for the expected traffic, vehicles and people, designing keyboards that accommodates the size of peoples’ fingers; surveying property; making zoning regions for city planning.)
• What are some patterns that you are aware of? How can patterns be used to make predictions that can in turn be used to solve problems?

Post-Introduction Assessment

Rectangle Problems: As part of the Introduction/Motivation content, students work in groups to fill out the Corral Fencing Worksheet. Given 300, 600 and 900 feet of fencing, students calculate perimeters and areas for the construction of square horse corrals. They use in-out tables to help them elicit the mathematical patterns. Direct groups to confer on their answers and make sure all members of the group understand and agree upon the answers, so they are prepared and comfortable presenting their solution to the class.

Lesson Summary Assessment

Discussion: As a class, discuss student’s answers to the Corral Fencing Worksheet. Ask groups to share their work (either verbally or on the classroom board). The groups chosen do not necessarily need to have the correct answer. After each group presents, see if anyone from the class has any comments. If a group is incorrect, see if another class member is able to correct them and explain any mistakes.

Suggested prompt questions:

• Do you agree with this group’s solution/explanation?
• Did anyone else get a different answer?
• Did someone solve this problem a different way?

Once all problems have been presented, check for understanding. To verify that students understand that area increases proportionally to the square of the factor the length is changed by, ask students: What would the area of a square corral be using 1,200 feet of fencing? Tell them to use the generalization rather than an equation to solve for the area. (Answer = 90,000 sq. ft.) Give students a few minutes to work on this with their groups and then regroup as a class and discuss.

Homework

Circle Problems: As homework, assign students to complete the Fire Pit Homework Worksheet. Similar to how students investigated squares during the lesson, the worksheet problems guide them to investigate the relationship between the radius of a circle and its area. Review their answers to assess their comprehension of the concepts.

Lesson Extension Activities

Have students look at similar patterns for 3D shapes. For example, challenge them to scale up and scale down the side dimensions of a cereal box and see how that affects surface area and volume of the box. To increase the challenge have them investigate the relationship between side length and surface area and volume of a rectangular prism.

References

Copyright

Contributors

Supporting Program

Acknowledgements

This activity was developed by CU Teach Engineering, a pathway to STEM licensure through the Engineering Plus degree program in the College of Engineering and Applied Science at the University of Colorado Boulder.