Quick Look
Grade Level: 4 (3-5)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00 This activity uses some non-expendable (reusable) items such as a LEGO MINDSTORMS EV3 robot and software; see the Materials List for details.
Group Size: 28
Activity Dependency: None
Subject Areas: Measurement, Science and Technology
NGSS Performance Expectations:

| 3-5-ETS1-2 |

Summary
Students develop and solidify their understanding of the concept of "perimeter" as they engage in a portion of the civil engineering task of land surveying. Specifically, they measure and calculate the perimeter of a fenced in area of "farmland," and see that this length is equivalent to the minimum required length of a fence to enclose it. Doing this for variously shaped areas confirms that the perimeter is the minimal length of fence required to enclose those shapes. Then students use the technology of a LEGO® MINDSTORMS® EV3 robot to automate this task. After measuring the perimeter (and thus required fence length) of the "farmland," students see the robot travel around this length, just as a surveyor might travel around an area during the course of surveying land or measuring for fence materials. While practicing their problem solving and measurement skills, students learn and reinforce their scientific and geometric vocabulary.Engineering Connection
Acting like engineers, students make measurements and use technology to characterize model land areas. The precise measurement of land boundaries is essential for a variety of civil engineering tasks such as the design of roads, bridges, retaining walls and other structures. Structural and agricultural engineers use similar techniques to create structures and efficient irrigation systems. Seeing how robots may help with land surveying highlights the potential of technology to assist in many engineering challenges. During the activity, students gain an understanding of how the perimeter of a shape is also the minimum distance around a shape, a crucial detail for many engineering applications.
Learning Objectives
After this activity, students should be able to:
- Determine the perimeter of shapes such as rectangles, squares and triangles.
- Explain how finding a perimeter is an important skill for civil engineers and others (for purposes such as land surveying, fencing, etc.).
- Describe the potential robots have for engineering applications.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
3-5-ETS1-2. Generate and compare multiple possible solutions to a problem based on how well each is likely to meet the criteria and constraints of the problem. (Grades 3 - 5) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Generate and compare multiple solutions to a problem based on how well they meet the criteria and constraints of the design problem. Alignment agreement: | Research on a problem should be carried out before beginning to design a solution. Testing a solution involves investigating how well it performs under a range of likely conditions. Alignment agreement: At whatever stage, communicating with peers about proposed solutions is an important part of the design process, and shared ideas can lead to improved designs.Alignment agreement: | Engineers improve existing technologies or develop new ones to increase their benefits, to decrease known risks, and to meet societal demands. Alignment agreement: |
Common Core State Standards - Math
-
Solve real world and mathematical problems involving perimeters of polygons, including finding the perimeter given the side lengths, finding an unknown side length, and exhibiting rectangles with the same perimeter and different areas or with the same area and different perimeters.
(Grade
3)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Explain the tools and techniques that people use to help them do things.
(Grades
Pre-K -
2)
More Details
Do you agree with this alignment?
State Standards
New York - Math
-
Solve real world and mathematical problems involving perimeters of polygons, including finding the perimeter given the side lengths, finding an unknown side length, and exhibiting rectangles with the same perimeter and different areas or with the same area and different perimeters.
(Grade
3)
More Details
Do you agree with this alignment?
New York - Science
-
Generate and compare multiple possible solutions to a problem based on how well each is likely to meet the criteria and constraints of the problem.
(Grades
3 -
5)
More Details
Do you agree with this alignment?
Materials List
Each class needs:
- LEGO MINDSTORMS EV3 robot, such as EV3 Core Set (5003400) at https://education.lego.com/en-us/products/lego-mindstorms-education-ev3-core-set/5003400#lego-mindstorms-education-ev3
- LEGO MINDSTORMS Education EV3 Software 1.2.1, free online, you have to register a LEGO account first; at https://www.lego.com/en-us/mindstorms/downloads/download-software
- computer, loaded with EV3 1.2.1 software
- Example EV3 Robot Line-Follow Program, for the teacher to use to program the robot
- whiteboard and dry erase pens (or the classroom board and chalk)
- colored tape, to create the outlines of three shapes on the floor (rectangle, square, triangle); it is best if the tape color is high-contrast to the floor color, such as dark tape on light floor or light tape on dark floor
- ruler or yardstick
- Fence That Farmland Pre-Quiz, one per student
- Fence That Farmland Post-Quiz, one per student
Note: This activity can also be conducted with the older (and no longer sold) LEGO MINDSTORMS NXT set instead of EV3; see below for those supplies:
- LEGO MINDSTORMS NXT robot, such as the NXT Base Set
- LEGO MINDSTORMS Education NXT Software 2.1
- computer, loaded with NXT 2.1 software
- Example NXT Robot Line-Follow Program, for the teacher to use to program the robot
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/nyu_farmland_activity1] to print or download.Pre-Req Knowledge
Some exposure to the term "perimeter," and basic familiarity with EV3 robots and programming.
Introduction/Motivation
Land surveying is an important task that civil engineers perform in order to better understand and describe particular areas of land. One part of surveying land is determining the boundary, or "perimeter" of the land area. Raise your hand if you have heard of the term "perimeter" before. (See how many students raise their hands.) Don't worry if this term is not familiar to you. By the end of our activity, you will be more comfortable with it. (Take out a whiteboard and dry erase pens, or use the classroom board.)
Let's talk about what "perimeter" means. The perimeter of a shape is just the length around the entire area. For example, the perimeter of a square is the length of each of the four sides added together. The perimeter of a triangle is the length of each of its three sides added together. And the perimeter of a circle is the length around that circle. Let's illustrate the concept of the perimeter on the board.
(Draw an arbitrary rectangle on the board.) If I want to find the perimeter of this rectangle, how might I do it? (Listen to student suggestions.) Would I shade the inside and figure out how much I shaded, or would I add up the lengths of the sides? (Listen to student responses.) That's right! I'd add up the lengths of the sides!
Now that we are a little more comfortable with the term "perimeter," let's talk about how we might find the perimeter of an area of land we are surveying. (Draw an arbitrary square on the board.) If this square was an area of land that I owned, how might I find the perimeter of it? (Take suggestions from the class.) You are all right; I would add up the lengths of the sides! And, if I was certain that my land was a square, I would only have to find the length of one of the sides and multiply it by four in order to determine the perimeter!
What might be some reasons why I would want to know the perimeter of my land? (Listen to student suggestions.) Those are awesome ideas! I might want to plant a garden or some crops, or put in a swimming pool, or be able to describe the size of my yard if I was selling my house. How might the knowledge of a perimeter also be useful to engineers? Well, if you were an engineer that had been tasked with designing a building that required a fence around the property using a minimum of materials, you would want to build a fence that enclosed just the perimeter and no more. Let me show you an example.
(Draw a triangle with three equal sides on the board.) Imagine this triangle is a piece of farmland that I own and I only own the area inside this triangle. If I wanted to make a fence around my farmland using a minimum of fencing, what would that fence look like? Would it look like a square? Or a triangle? Why or why not? (Draw a square around the triangle, and demonstrate that the triangle has a shorter perimeter than the square around the triangle by using a ruler to make measurements of both perimeters and comparing those measurements.)
Does anyone think that he or she can draw a shape other than this triangle that completely encloses my farm, but uses less fencing? (If any student thinks s/he can, let him/her demonstrate or explain, and correct as necessary.)
Now we all understand that only the perimeter of a shape provides the minimum distance around it, and that this is an important concept for engineers (and others) to master.
During today's activity, you will get a chance to see how important perimeter measurement is by measuring perimeters yourselves. We will measure the perimeter of various areas of "farmland" in order to find the minimum amount of fencing you would need to enclose them!
Then, we will use this robot (show the LEGO robot) to illustrate how robots might be used to help engineers to survey land! Why might it be useful to have a robot travel around the perimeter of a piece of land? (Listen to student ideas.) Those are fantastic ideas! Robots could take measurements so you can figure out how much fencing material is needed to enclose a piece of property, look for any problems or breaks in the stretch of fencing around a piece of land, and measure the land perimeter to verify or correct a previous measurement.
Procedure
Before the Activity
- Follow the instructions provided in the LEGO base set to build and program a basic robot with a color sensor installed. Then, program the robot using the Example Robot Line-Follow Program.
- Gather materials and make copies of the Fence That Farmland Pre-Quiz and Fence That Farmland Post-Quiz, one each per student.
- Decided whether you want to prepare the tape shapes on the floor before the activity or with the students during the activity. To do this, use colored tape to make outlines of three shapes—rectangle, square, triangle—in dimensions of your own choosing, on a smooth floor area of the classroom or hallway. Linoleum floors work well.
With the Students
- Hand out and have students complete the pre-quiz. Collect the completed quizzes.
- Discuss the concept of perimeter with students, as presented in Introduction/Motivation section.
- As a class, walk through several perimeter-measuring examples of different shapes. If not already done, use colored tape to create square, rectangle and triangle shapes on the floor.
- Discuss as a class some strategies for measuring perimeters. Have students demonstrate different ways of measuring and other ideas they might have. Emphasize that real land surveying civil engineers might think about these things in order to simplify their tasks. For example, for a square, one could multiply the length of one side of the square four times to find its perimeter. Or, for a rectangle, multiply the lengths of two adjacent sides twice.
- Choose a few students to use a ruler or yardstick to assist in the measurement of each of the three shapes on the floor. Ask other students to record and tally the lengths of the sides as they are measured.

A robot travels the perimeter of triangle. - After students successfully determine the perimeters of the shapes, ask them what the minimum distance of fencing around each shape would be. To cement and verify their understanding, ask them to explain what shape the minimum amount of fencing would be, and why it would be equal to the distance they specified.
- Upon successful explanation of the minimum distance of fencing required, let students know they have "earned" the privilege of watching the robot follow the shapes' perimeters on the floor. Ask students what sort of variables the robot needs to know. (Answers: Where to start, where to end, the angle of the triangles, etc.) Help students place the robot on the tape and initiate the line follow program.
- Ask students to think of reasons why robots might be useful to engineers. (Expect students to suggest: Faster and more accurate measurements, ability to go places that people cannot, etc.)
- Discuss with the class other types of engineering or situations that might use robots. (Possible answers: Nuclear engineers use them to survey dangerous sites. Mechanical engineers use them to install very small parts. Environmental engineers use them to navigate low-oxygen climates. Aerospace engineers use robots to explore other planets.)
- Administer the post-quiz in class or as a homework assignment.
Vocabulary/Definitions
area: The amount of space inside the boundary of a flat (two-dimensional) object such as a triangle, rectangle or circle.
dimension: A measure of space in a given direction, such as width, height or length.
perimeter: The length or distance around the outer edge of a shape.
triangle: A figure formed by connecting three points not in a straight line by straight-line segments; a three-sided polygon.
Assessment
Pre-Activity Assessment
Pre-Quiz: Before starting the activity, administer the four-question, multiple-choice Fence That Farmland Pre-Quiz. Review students' answers to gauge their base knowledge of the activity subject matter.
Activity Embedded Assessment
Questions: In your exchanges with students during the Procedure section steps, ask students the provided questions, using their answers to gauge their comprehension.
Post-Activity Assessment
Post-Quiz: At activity end, administer the four-question, multiple-choice Fence That Farmland Post-Quiz, which is similar, but not exactly the same, as the pre-quiz. Review students' answers to gauge their comprehension of the activity content.
Investigating Questions
- What do civil engineers learn from surveying the perimeter of land areas? (Answer: Civil engineers learn the minimum distance around a piece of land, which may be important in construction or fencing for that area of land.)
- How can you determine the perimeters of shapes such as squares, rectangles and triangles? (Answer: Add up the lengths of the shapes' sides to determine their perimeters.)
- What tricks or short-cuts are used to measure such shapes? (Answer: If similar sides are present in the shape, one can multiply their lengths instead of measuring each individually.)
- Why is the correct measurement of perimeter important? (Answer: Perimeter measurement is important because it determines the distance around areas of land, which is needed for real estate transactions, construction, agriculture, irrigation, etc.)
- For what purposes might you use perimeters in your daily lives? (Possible answers: To fence a playground, dog run, garden, running track or football field; to know how much trim to buy for the edge of a skirt or lamp shade; to get the right amount of rope to mark the boundary lines of a sand volleyball court; to know how much baseboard trim to buy for the bottom of the wall edges of a room; to know how much molding trim material to buy to frame a photograph.)
Troubleshooting Tips
The provided EV3 LEGO robot program works within a somewhat generous tolerance for dark tape on a light background floor or light tape on a dark background, assuming high contrast. If the settings do not seem to be working, modify the "Switch - Color Sensor" block settings by increasing or decreasing from the suggested default value of "50." As a reference, the color sensor typically gives readings less than 50 on darker backgrounds, and readings greater than 50 on lighter backgrounds.
Activity Scaling
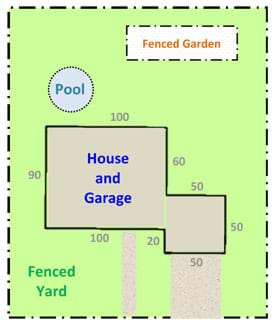
For lower grades, help students through the math of adding up the sides of their shapes, and be forthcoming about measurement tricks and techniques for different shapes.
For upper grades, have students:
- Draw their own shapes (including polygons with more sides) and find the perimeters using at least two different techniques.
- Measure the perimeters of objects in the classroom (desktops, countertops, tabletops, doorway openings, window frames, ceiling light fixtures).
- Apply their newfound knowledge of the minimum fence length of their shapes to construct actual miniature fences made of paper and tape.
- Measure the perimeters of their homes or yards as a weekend homework assignment.
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Through this lesson and its two associated activities, students are introduced to the use of geometry in engineering design, and conclude by making scale models of objects of their choice. In this lesson, students complete fencing (square) and fire pit (circle) word problems on two worksheets—which ...

Students learn about trigonometry, geometry and measurements while participating in a hands-on interaction with LEGO® MINDSTORMS® technology. First they review fundamental geometrical and trigonometric concepts. Then, they estimate the height of various objects by using simple trigonometry. Students...
Copyright
© 2014 by Regents of the University of Colorado; original © 2011 Polytechnic Institute of New York UniversityContributors
Ursula KonigesSupporting Program
AMPS GK-12 Program, Polytechnic Institute of New York UniversityAcknowledgements
This lesson was developed by the Applying Mechatronics to Promote Science (AMPS) Program funded by National Science Foundation GK-12 grant no. 0741714. However, these contents do not necessarily represent the policies of the National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: October 16, 2020




User Comments & Tips