Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Expendable Cost/Group: US $5.00
Group Size: 4
Activity Dependency:
Subject Areas: Physical Science
NGSS Performance Expectations:

| MS-ETS1-1 |
Summary
Through a series of activities, students discover that the concept of mechanical advantage describes reality fairly well. They act as engineers creating a design for a ramp at a construction site by measuring four different inclined planes and calculating the ideal mechanical advantage versus the actual mechanical advantage of each. Then, they use their analysis to make recommendations for the construction site.
Engineering Connection
It is important for engineers to know the measured effectiveness of the tools they use. While effectiveness can be learned through experience, it can also be calculated theoretically. An inclined plane is a simple machine often used in engineering activities (usually construction), and its associated mechanical advantage helps engineers design devices so work can be done efficiently and effectively. Measuring mechanical advantage helps engineers optimize a design so that the best possible solution to a mechanical problem is achieved. Engineers have to often design the temporary supports and structures for bridges and buildings, which may include several of the simple machines.
Learning Objectives
After this activity, students should be able to:
- Calculate the mechanical advantage of an inclined plane in two different ways.
- Explain why the concept of mechanical advantage is useful for engineers.
- Perform engineering design work in a group.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-ETS1-1. Define the criteria and constraints of a design problem with sufficient precision to ensure a successful solution, taking into account relevant scientific principles and potential impacts on people and the natural environment that may limit possible solutions. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Define a design problem that can be solved through the development of an object, tool, process or system and includes multiple criteria and constraints, including scientific knowledge that may limit possible solutions. Alignment agreement: | The more precisely a design task's criteria and constraints can be defined, the more likely it is that the designed solution will be successful. Specification of constraints includes consideration of scientific principles and other relevant knowledge that is likely to limit possible solutions. Alignment agreement: | All human activity draws on natural resources and has both short and long-term consequences, positive as well as negative, for the health of people and the natural environment. Alignment agreement: The uses of technologies and any limitations on their use are driven by individual or societal needs, desires, and values; by the findings of scientific research; and by differences in such factors as climate, natural resources, and economic conditions.Alignment agreement: |
Common Core State Standards - Math
-
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities. Describe patterns such as clustering, outliers, positive or negative association, linear association, and nonlinear association.
(Grade
8)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Interpret expressions that represent a quantity in terms of its context
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Make two-dimensional and three-dimensional representations of the designed solution.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Apply the technology and engineering design process.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Direct and indirect measurement can be used to describe and make comparisons.
(Grade
8)
More Details
Do you agree with this alignment?
-
Construct and interpret scatter plots for bivariate measurement data to investigate patterns of association between two quantities.
(Grade
8)
More Details
Do you agree with this alignment?
-
Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Interpret expressions that represent a quantity in terms of its context.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in applied problems.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Colorado - Science
-
Predict and evaluate the movement of an object by examining the forces applied to it
(Grade
8)
More Details
Do you agree with this alignment?
-
Use mathematical expressions to describe the movement of an object
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
For whole class:
- 8 clamps and stands
- 8 plywood sheets about 10 cm (4 in.) wide and 2 each of the following lengths: 30 cm, 60 cm, 90 cm, and 120 cm.
Each group needs:
- spring scale
- meter stick
- small car (i.e., rolling toy) with a string attached
- weight (same size for each group)
- 4 copies of the Inclined Plane Worksheet
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_simp_machines_lesson02_activity1] to print or download.Introduction/Motivation
Can you think of a situation when an inclined plane would be useful? (Students should volunteer some ideas; all ideas should be respectfully heard.) Perhaps when you are moving a heavy piano onto a performance stage or furniture out of a truck? Or perhaps when it is not possible to walk up/down stairs and you need a wheelchair?
Have you ever seen the progress of a structure on a construction site? Sometimes you will see temporary ramps, supports and ledges in place, made out of wood and other inexpensive materials. Did you know that engineers help design those temporary devices? Construction management on a building site is a component of civil engineering. Why might it be important to have an engineer design temporary supports? Well, it is important to have someone who knows what will be sturdy and safe for the workers on the site. Imagine you are an engineer who has been asked to help design some temporary working areas at a construction site, including a ramp to help workers move heavy wheelbarrows of dirt and crushed concrete. The workers pushing the wheelbarrow apply an average force of 23 kg (50 lbs) and they must move the wheelbarrow 30 meters in elevation. What could you, the engineer, use to design an inclined plane to help them complete their job? (Answer: The concept of mechanical advantage for inclined planes.)
What does mechanical advantage mean again? That's right: it's the factor by which the force is lessened or the degree to which a machine makes work easier. The mechanical advantage of all machines is defined by the general expression:
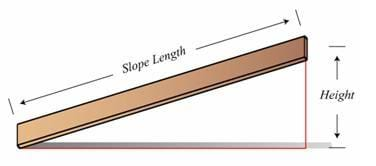
However, this expression is usually too general. The inclined plane gets its mechanical advantage by moving some object over a long gradual incline rather than moving it over a much shorter vertical path. Therefore, the input distance is equal to the slope length, and the output distance is the overall height of the inclined plane. In other words, by moving the load along the length of the slope, it is raised a vertical distance equal to the height of the inclined plane. Now, the mechanical advantage equation of the inclined plane is rewritten as:
Is this calculation always right? Well, another way to find the mechanical advantage of an inclined planed is found by measuring the force used to move an object up an inclined plane. We call this the actual mechanical advantage. Looking back at our first equation, the output force is equal to the force needed to lift the object straight up the same distance (or the resistance force); the input force is equal to the amount of force needed to move the object up the ramp (or the effort force). What is different about the actual mechanical advantage? Well, the actual mechanical advantage is quite different from the theoretical mechanical advantage since it accounts for friction, and there is no way to know it until after the work is already done.
We have now learned how to calculate the mechanical advantage for inclined planes. Today, we are going to work on the engineering problem of designing a ramp at a construction site to move a load (a wheelbarrow) to a certain height. We are going to test the calculations we learned for mechanical advantage. Do these calculations actually predict what happens in the real world? Today we are going to find out!
Procedure
Before the Activity

- Gather the materials and make copies of the Inclined Plane Worksheet
- Set up the classroom with 4 designated inclined plane stations. Set up 2 inclined planes of the same size at each station. Place two clamps/stands at each station and set each clamp to 20 cm (height). Clamp the planes to each stand, as illustrated in Figure 2.
With the Students
- Break students into groups of 4.
- Give each student a copy of the Inclined Plane Worksheet to complete.
- Distribute supplies to each group (spring scale, meter stick, car and weight).
- Have students follow the instructions on the Inclined Plane Worksheet. The following two tasks need to be repeated for each sized inclined plane. (Note: students should have 4 sets of data.):
- Measure the height and length of the plane, as shown in Figure 3, and calculate the mechanical advantage using this information. (optional: Instead of measuring the incline length, calculate it by using the Pythagorean Theorem by measuring the height and the length of the ramp along the table)
- Measure the force it takes to move the weight by attaching the spring scale to the weight and lifting it into the air. Record this measurement as output force. Then, put the weight into the car and pull the car up the ramp with the spring scale, as shown in Figure 4. Record this from the spring scale in grams as input force. Calculate the actual mechanical advantage using this information.

- Have students answer the following analysis questions on the Inclined Plane Worksheet.
- Did you obtain different mechanical advantages for the different methods of measuring? If so, was the difference large or small?
- Which inclined plane had the greatest mechanical advantage?
- Does calculating mechanical advantage just with the dimensions of the inclined plane really work? That is, does the calculation describe what really happens?
- If you were the engineer designing a ramp for a construction site to move a wheelbarrow a height of 30 meters, which inclined plane would you use? Why?
- What are some possible sources of error in this experiment?
Assessment
Pre-Activity Assessment
Class Discussion: Solicit, integrate and summarize student responses.
- Have the students generate a list of inclined planes. (Some examples include: wheelchair ramps, escalators, stairs, highways, boat ramps, draw bridges and hiking trails.)
- What does mechanical advantage describe? (Answer: A simple machine's mechanical advantage describes the decrease in force needed to do the same amount of work.)
Activity Embedded Assessment
Group Question: During the activity, ask the groups:
- Should the mechanical advantage of an inclined plane be the same no matter which way it is measured? (Answer: yes)
- Should the mechanical advantage of an inclined plane be the same for different lengths of inclined planes (Answer: no)
Inclined Plane Worksheet: Instruct the students to record measurements and follow along with the activity on their Inclined Plane Worksheet. After students have finished their worksheet, have them compare answers with their peers.
Post-Activity Assessment
Class Discussion: Review and discuss the worksheet answers with the entire class. Use the answers to gauge students' mastery of the subject. Ask students to explain which inclined plane they would use as the engineer designing a ramp for a construction site to move a wheelbarrow a height of 30 meters. What types of engineering constraints might they encounter when designing this temporary support structure? (Possible answers might include: physical limitations, expense, time and safety.)
Graphing: Have students graph the length of incline vs. the theoretical Mechanical Advantage. Discuss relationship and/or patterns.
Problem Solving: Have students work in pairs to solve the following problem.
- Erza has a piano concert tonight in the school auditorium. He needs to move the concert piano up four feet to the stage. The piano weighs 900 lbs and is on wheels. About how long a ramp should he use to push it up to the stage? Assume Ezekiel can push 150 lbs. (Answer: 24 feet)
- Given that we want the mechanical advantage to be 6 and the length of a ramp to be 160 m, find the formula to determine the needed height H of the ramp.
- Given that we want the mechanical advantage to be 4 and the height of the ramp to be 80, find the formula to determine the needed length L of the ramp."
Troubleshooting Tips
If students are having trouble reading the spring scales, tell them to pull on it consistently.
Some students may ask if the wheels on the cars have any affect on the mechanical advantage of the inclined plane. The answer is no. The wheel-and-axle simple machine has to do with applying a force to the wheel as in turning a doorknob. For those cars moving up a plane, the force is applied to the cart and axle, not the wheel. So the wheel-and-axle is not a simple machine in the sense that we talk about it in this unit. It is the same as the difference between users rolling their wheelchairs by pushing on the wheel vs. the Flintstones pushing their car with their feet, wherein you do not apply any force to the wheel as such. The wheels reduce friction for the cars moving up the plane to model the frictionless environment that is assumed by the MA calc for the inclined plane. Used in this way, the wheel-and-axle per say is not a simple machine. You can read more about the mechanical advantage of the wheel-and-axle in Lesson 3 of this associated unit. The actual mechanical advantage is quite different from the theoretical mechanical advantage since it accounts for friction, and there is no way to know it until after the work is already done.
Activity Extensions
Journal Entry: Write a journal entry that answers the question: What is mechanical advantage? Write another sentence on why you think engineers would find it useful to know the mechanical advantage of a particular tool or piece of equipment. Write another sentence that begins with "For example, ..." and describe a situation where you think an engineer might use mechanical advantage.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

This lesson introduces students to three of the six simple machines used by many engineers. These machines include the inclined plane, the wedge and the screw.

Students are introduced to three of the six simple machines used by many engineers: lever, pulley, and wheel-and-axle. In general, engineers use the lever to magnify the force applied to an object, the pulley to lift heavy loads over a vertical path, and the wheel-and-axle to magnify the torque appl...

Students explore building a pyramid, learning about the simple machine called an inclined plane. They also learn about another simple machine, the screw, and how it is used as a lifting or fastening device.

In this lesson, students learn about work as defined by physical science and see that work is made easier through the use of simple machines. Already encountering simple machines everyday, students will learn about their widespread uses in improving everyday life.
References
U.S. Department of Transportation, Federal Transit Administration, accessed September 4, 2007. http://www.fta.dot.gov/
Copyright
© 2007 by Regents of the University of Colorado.Contributors
Michael Bendewald; Jake Lewis; Malinda Schaefer Zarske; Janet YowellSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado at BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education, and National Science Foundation GK-12 grant no 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: August 28, 2023








User Comments & Tips