Quick Look
Grade Level: 8 (7-9)
Time Required: 45 minutes
Expendable Cost/Group: US $5.00
Group Size: 3
Activity Dependency:
Subject Areas: Physical Science
NGSS Performance Expectations:

| MS-ETS1-1 |
Summary
In this activity, students gain first-hand experience with the mechanical advantage of pulleys. Students are given the challenge of helping save a whale by moving it from an aquarium back to its natural habitat into the ocean. They set up different pulley systems, compare the theoretical and actual mechanical advantage of each and discuss their recommendations as a class.
Engineering Connection
Engineers need to know the measured effectiveness of the tools they use. This can be learned through experience or calculated theoretically. A pulley is a simple machine often used in engineering activities and accordingly has a measurable effectiveness, or mechanical advantage. Pulleys are good machines for lifting heavy objects over a direct vertical path. Pulleys are often incorporated into the design of various engineering systems such as the crane, where huge loads are manipulated with a little force supplied by a relatively small motor. Cranes can be seen moving buildings, boats, large animals, and even swimming pools.
Learning Objectives
After this activity, students should be able to:
- Calculate the mechanical advantage of a pulley.
- Explain why the concept of mechanical advantage is useful for engineers.
- Perform engineering design work in a group.
Educational Standards
Each Teach Engineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each Teach Engineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in Teach Engineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
| NGSS Performance Expectation | ||
|---|---|---|
|
MS-ETS1-1. Define the criteria and constraints of a design problem with sufficient precision to ensure a successful solution, taking into account relevant scientific principles and potential impacts on people and the natural environment that may limit possible solutions. (Grades 6 - 8) Do you agree with this alignment? |
||
| Click to view other curriculum aligned to this Performance Expectation | ||
| This activity focuses on the following Three Dimensional Learning aspects of NGSS: | ||
| Science & Engineering Practices | Disciplinary Core Ideas | Crosscutting Concepts |
| Define a design problem that can be solved through the development of an object, tool, process or system and includes multiple criteria and constraints, including scientific knowledge that may limit possible solutions. Alignment agreement: | The more precisely a design task's criteria and constraints can be defined, the more likely it is that the designed solution will be successful. Specification of constraints includes consideration of scientific principles and other relevant knowledge that is likely to limit possible solutions. Alignment agreement: | All human activity draws on natural resources and has both short and long-term consequences, positive as well as negative, for the health of people and the natural environment. Alignment agreement: The uses of technologies and any limitations on their use are driven by individual or societal needs, desires, and values; by the findings of scientific research; and by differences in such factors as climate, natural resources, and economic conditions.Alignment agreement: |
Common Core State Standards - Math
-
Use proportional relationships to solve multistep ratio and percent problems.
(Grade
7)
More Details
Do you agree with this alignment?
-
Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.
(Grade
7)
More Details
Do you agree with this alignment?
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Make two-dimensional and three-dimensional representations of the designed solution.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
-
Apply the technology and engineering design process.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
Colorado - Math
-
Solve real-world and mathematical problems involving the four operations with rational numbers.
(Grade
7)
More Details
Do you agree with this alignment?
-
Use proportional relationships to solve multistep ratio and percent problems.
(Grade
7)
More Details
Do you agree with this alignment?
-
Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients.
(Grade
7)
More Details
Do you agree with this alignment?
Colorado - Science
-
Predict and evaluate the movement of an object by examining the forces applied to it
(Grade
8)
More Details
Do you agree with this alignment?
-
Use mathematical expressions to describe the movement of an object
(Grade
8)
More Details
Do you agree with this alignment?
Materials List
Each group needs:
- Approximately 20 feet of nylon rope
- Two-wheeled pulley
- Single pulley
- Spring scale
- String
- Weight (can use soup cans, rocks, weights, etc.)
- 3 copies of the Pulley Worksheet
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/cub_simp_machines_lesson03_activity1] to print or download.Pre-Req Knowledge
Students should be familiar with the six simple machines, as discussed in Lesson 1 of this unit,"The Advantage of Machines." Also, students should have some understanding of basic mechanical advantage.
Introduction/Motivation
What are some examples of tools? (List students' answers on the chalk/white board.) There are many different kinds of tools: hand tools, power tools, big tools, small tools, tools with specific uses, tools with many uses, and so on. What is a good way to define a tool — a definition that includes all of these examples? Should it include work? (Write students' definitions on the chalk/white board. Their answers should be something similar to: a tool is a thing used by people while doing work.)

One example of a simple tool is a pulley. (Show the class a pulley.) Who knows its purpose? (Answer: A pulley is usually used for lifting something up, sometimes pulling something.) How can we measure the effectiveness of a system of pulleys? (Answer: We would calculate the mechanical advantage.) The mechanical advantage of all six simple machines is defined by the general expression:
However, this expression is usually too general.
The most precise method for calculating the mechanical advantage of a pulley is by counting the number of ropes or cables that support the load. Then the mathematical relationship is simply expressed as:
There is another way to determine mechanical advantage though. We can measure it directly by measuring the decrease in force used to lift an object. Let's refer to this as the actual mechanical advantage.
The mechanical advantage of pulleys has been used by engineers for thousands of years. Archimedes (b. 287 BC, d. 212 BC) was a Greek thinker and engineer. When Rome was attacking Syracuse (where Archimedes lived), he devised a pulley attached to a great lever that extended over a rock wall and dangled a giant hook. When Roman ships approached, the hook was lowered, grabbing the ships. The pulley then lifted the huge ships out of the water, only to drop them back down with a devastating crash. Since then, countless engineers have used pulleys to lift heavy objects for a variety of different purposes. Pulleys designed by engineers can be found on assembly lines, construction sites and other places where heavy objects need to be moved.
We have now learned how to calculate mechanical advantage for pulleys. Today, we are going to work on an engineering scenario that has actually happened in years past. For our activity today, imagine that Marine biologists at an aquarium in California have been working to save a sick gray whale that was found off the coast of Big Sur. The gray whale has been in their care for several months and is now completely healthy. We work at the engineering firm that they have hired to design a lift that will safely remove the whale from the aquarium and move it back into its natural environment. We will need to design a system that can lift the 16 ton (32,000 pound) whale to a certain height in order to be moved back into coastal waters.
As engineers, we know that there are several steps that need to be completed in the design of a solution for any technical problem. The first step in designing a proper solution is to recognize the need. Who is the customer that we need to make happy? In this case, it is the aquarium, the whale, and perhaps the citizens who have been keeping track of the whale's story in the news.
The next step is defining the problem needs. What is one way that we could phrase this problem with moving the whale? (Discuss with the class. Answers should not limit the solutions, so one idea may be: get the whale back to the ocean safely.) Next, an engineer would think about information that might help to solve the problem. Needed information might include the constraints or limitations on the problem, such as money or time the whale can be out of the water, but we would also consider what we need to know to solve the problem.
Today, we are going to look at various pulleys as a way to lift the whale out of the tank in the aquarium. We will be setting up different pulley systems and examining if the theoretical mechanical advantage is the same as the actual. We are going to test the calculations we make for the mechanical advantage of the pulleys. We will learn if these calculations actually predict what happens in the real world. After we learn about pulleys and their mechanical advantage, we will brainstorm ideas for the whale lift to present to the aquarium.
Procedure
Before the Activity
- Gather materials.
- Make copies of Pulley Worksheet.
With the Students
- Distribute materials and the Pulley Worksheet.
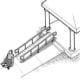
- Allow students to stand on desks or ladders to hang the two-wheeled pulley on the ceiling, as shown in Figure 3.

- Have the students follow the instructions on the Pulley Worksheet for measuring the weight (load) of the object, effort and mechanical advantage of several pulley systems.
- Have the students discuss the theoretical mechanical advantages in comparison to the actual ones.
- Lastly, engage the students in discussion of their activity. What were some possible sources of error in their procedure? What recommendations would they make as engineers to the aquarium trying to move the gray whale back to the ocean? Would they use pulleys? What are some constraints that they as engineers might consider while designing a pulley system for the whale? What impacts to the whale might they need to consider for moving it back to the ocean
Assessment
Pre-Activity Assessment
Brainstorming: In small groups, have the students engage in open discussion. Remind students that no idea or suggestion is "silly." All ideas should be respectfully heard. Ask the students:
- How many devices can you think of that contain pulleys? (Some examples include: assembly lines, cranes, construction sites and other places where heavy objects need to be moved.)
Activity Embedded Assessment
Worksheet: Have the students record measurements and follow along with the activity on their Pulley Worksheet. After students have finished their worksheet, have them compare answers with their peers.
Question/Answer: Ask students questions and have them raise their hands to respond. Write answers on the board and discuss as a class.
- Are the theoretical and actual mechanical advantages similar for each pulley system? (Have students answer on their worksheet.)
Post-Activity Assessment
Design Requirements and Constraints: Have the students make a list on the board of the problem's design requirements and constraints. Some examples might include: budget for materials, time, safety and impact on the whale, ethical and social impacts.
Engineering Design: Engineers need to be able to communicate their ideas effectively to their audience. Have students create a design of their pulley system on a blank sheet of paper for the aquarium. What recommendations would they make as engineers to the aquarium trying to move the gray whale back to the ocean? What is some other information they might want to know in order to design their lift effectively?
Journal Writing: Have students write a journal entry on the results of the activity. The entry should summarize the results and discuss why knowing the mechanical advantage of a machine is useful.
Safety Issues
Remind students to be cautious when standing on desks to hang their pulleys. They should NOT rock their desks or try to jump from desk to desk.
Troubleshooting Tips
If students are having trouble reading the spring scales, tell them to pull on it consistently.
Activity Extensions
Have students research the Greek thinker and engineer Archimedes. What did he invent? Which of his inventions include one or more simple machines?
Subscribe
Get the inside scoop on all things Teach Engineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to three of the six simple machines used by many engineers: lever, pulley, and wheel-and-axle. In general, engineers use the lever to magnify the force applied to an object, the pulley to lift heavy loads over a vertical path, and the wheel-and-axle to magnify the torque appl...

This lesson introduces students to three of the six simple machines used by many engineers. These machines include the inclined plane, the wedge and the screw.

Students act as engineers creating a design for a ramp at a construction site by measuring four different inclined planes and calculating the ideal mechanical advantage versus the actual mechanical advantage of each.

Students learn how a pulley can be used to change the direction of applied forces and move/lift extremely heavy objects, and the powerful mechanical advantages of using a multiple-pulley system. Students perform a simple demonstration to see the mechanical advantage of using a pulley, and they ident...
References
U.S. Department of Transportation, Federal Highway Administration, Bridge Technology, "Accelerated Bridge Construction," July 7, 2006, accessed August 31, 2007. http://www.fhwa.dot.gov/bridge/crane27.htm
Copyright
© 2007 by Regents of the University of Colorado.Contributors
Michael Bendewald; Jake Lewis; Malinda Schaefer Zarske; Janet YowellSupporting Program
Integrated Teaching and Learning Program, College of Engineering, University of Colorado BoulderAcknowledgements
The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education, and National Science Foundation GK-12 grant no 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.
Last modified: October 6, 2023





User Comments & Tips