Hands-on Activity Determining Densities

Learning Objectives

After this activity, student should be able to:

• Describe a method for determining the density of an object or material that has a simple geometric shape (rectangular prism, sphere or cylinder).
• Describe a method for determining the density of an object or material that has a complex geometric shape.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Materials List

• An assortment of small objects with regular shapes; their densities will be determined by first measuring dimensions and then calculating volumes. For this assortment, gather objects with regular shapes (rectangular prisms, spheres, cylinders) such as metal bars, brass weights, wooden blocks, marbles, Fire Balls™ candy, wine corks, candles, art gum erasers, large crayons with pointed ends cut off, Styrofoam™ spheres (from craft supply shops) and modeling clay molded into cubes or spheres. Be sure to include some objects that float.
• A second assortment of objects that have irregular shapes; their volumes will be determined by the displacement of water. For this assortment, gather items such as rocks; small figurines (plastic soldiers or animals, metal or ceramic figures, but make sure they have no hollow portions and are made of only one material); large nails, nuts or bolts; short lengths of metal chain; pieces of broken brick, pottery, plastic or Styrofoam™ (if spheres are not used in the other assortment); rubber test tube or flask stoppers; and chunks of vegetables such as carrots or potatoes.
• rulers, at least one per team
• calculators, one per team
• balances accurate to at least 0.1 g (such as standard triple beam balances), one per team
• 25, 50 and 100 ml graduated cylinders, at least one per team (ideally one small one plus one of larger one per team)
• 250 and/or 500 ml beakers, one or both per team
• pans or trays to catch water that overflows from the beakers, one per team
• (optional) funnels to fit into the tops of the graduated cylinders (helpul to limit the amount of spilled water), one per team
• sponges and/or dishrags (for wiping up drips and spills), at least one per team
• thread

Worksheets and Attachments

Pre-Req Knowledge

• Students should be able to use rulers to measure lengths to the nearest millimeter, triple beam balances to measure masses to at least the nearest 0.1 gram, and graduated cylinders to measure liquids to at least the nearest 1 milliliter.
• Students should be able to calculate the volumes of rectangular, cylindrical and spherical solids.
• Students should be able to graph points on x-y coordinate grids.

Introduction/Motivation

(The associated lesson Introduction, in which students determine the density of a rectangular box filled with an unknown substance, provides adequate introduction to the activity as well. To further motivate students, add the following specific introductory information.)

Today I have a great variety of different objects for you to determine their densities. Some of the materials have what scientists call "known densities." In other words, their densities have been calculated to a high degree of accuracy in a lab, using sophisticated measuring devices.

After you have determined the densities of the objects, you can compare your results to the known densities. So, your challenge is to measure and weigh your objects very carefully, so your results are very close to the known densities.

Procedure

Part 1: Regular Shapes

1. Make copies of the Determining Densities Datasheet and give one to each student.
2. With students working in teams of four students each, direct them to determine the densities of the objects in the first assortment, items with regular shapes.
3. The method involves direct measurement of the volumes of the objects because they have simple geometric shapes.
4. Direct students to use the Determining Densities Datasheet to enter results for each object, rounding densities to the nearest one-hundredth.
5. Expect different teams to get slightly different densities for the same objects. This provides a good opening to discuss why these differences occur. (Refer to the Investigating Questions and Troubleshooting Tips sections). If two teams get very different densities, however, it suggests a measurement error, and the students involved should repeat their measurements and calculations.

Part 2: Irregular Shapes

Present the class with the second assortment of objects, whose shapes are not regular.

1. Direct students to work within their groups to figure out a way to determine the densities of these oddly shaped objects. Give them plenty of time to explore this problem (5-10 minutes, perhaps). If they cannot come up with the water-displacement method on their own, ask them to imagine filling a bathtub all the way to the top. Then ask what would happen if they took a gallon jug of juice and lowered it into the water. How much water would spill over the edge of the tub? What if they lowered themselves into the filled tub of water until they were completely submerged? How much water would spill out? Would it be possible to catch and measure the amount of water that spilled out?
2. Point out that liquid volumes are measured in liters or milliliters, but solid volumes are measured in meters or centimeters cubed. By a fortunate coincidence, however, 1 milliliter of water equals 1 cubic centimeter of water. (Students could also determine this for themselves.) This means that using standard laboratory graduated cylinders to measure displaced water allows for a very easy conversion of the volume of displaced water to the volume of the object. The volume in milliliters is simply the same as the volume in cubic centimeters, with the latter being the proper unit for density.
3. Make the beakers, graduated cylinders, trays and funnels available to students so that they can devise their own water-displacement methods to determine the volumes of the oddly shaped objects. If students have trouble devising an accurate method, offer suggestions, but let them do some problem solving on their own before stepping in. The idea is for students to place a beaker on the tray, and then use one of the other containers to fill the beaker with water to the point where it just begins to overflow. Have students wait for any last overflow dripping to stop before placing an empty container at the beaker's spout to catch the soon-to-be displaced water. Expect students to discover that they need to lower the object into the beaker gently to avoid splashing, since splashed water affects the amount of displaced water collected.
4. For the smaller objects, students may be able to simply submerge the object into a partially filled graduated cylinder. The change in water level equals the volume of the submerged object. This method is more accurate than measuring water that has spilled out an overflowing beaker.
5. You may need to remind students of the need for accuracy, not only in the weighing of the objects, but also in measuring the volume of displaced water. Using the smallest graduated cylinder possible allows for a more accurate measurement. Ask students to estimate the volume of water that will be displaced, and match the size of the graduated cylinder to the estimate.
6. You might also need to ask students which they should do first: find the mass of the object or find its volume. They should be able to reason that the objects will be weighed more accurately if they are weighed first, since that way they will be completely dry and no water will add to the mass.
7. For any of the objects that float, students have another problem to solve. They may try using a pencil point to hold the object just below the surface of the water. They could also use thread to tie the object to another, heavier object that sinks, such as a rock or piece of metal. If they do this, they need to subtract the volume of the rock or metal from the displaced volume of water in order to obtain the volume of the otherwise floating object.
8. As in Part 1, create a large data table on the board with room for all teams to enter their results, rounding their densities to the nearest one-hundredth. Have any teams with widely disparate results repeat their measurements and calculations.
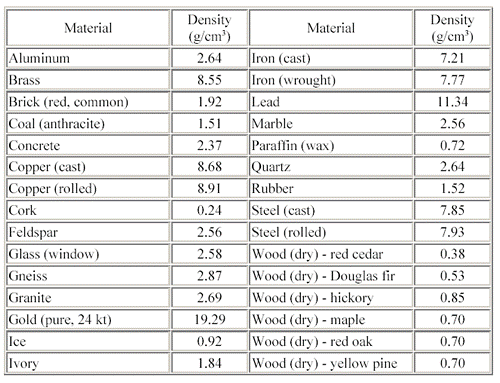
9. Refer to Table 1 to compare student results to known densities of common materials. If the materials are known, students can compare the accuracy of their determinations to the known values in the table. If the materials are not known, students may be able to speculate about their composition based on the table values.

Part 3: Density of Water and Graphing of Results

1. After students have determined the densities of the objects, ask them to find one more density, that of water. They may be puzzled at first, but give them time to realize that, just like the solid objects, they only need to find the mass of a known volume of water. (If needed, remind them to subtract the mass of the water container.) Check their results to make sure they get a density close to 1.00.
2. Next, have each student create a scatter graph for the objects, in which mass in grams is on the x-axis, and volume in cubic centimeters is on the y-axis. The graphs should look something like Figure 1. Have students add to their graphs the dashed line that forms the diagonal. Explain that this represents the density of water, since for pure water, the mass in grams is equal to its volume in cubic centimeters. Put another way, the ratio of mass to volume is approximately 1 g/cm³ at room temperature and pressure, as long as the units are grams and cubic centimeters (cm³).

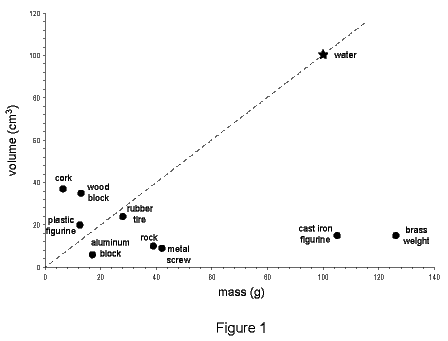
3. Have students examine their completed graphs. Ask what the points that lie above the dashed line have in common. Although there may only be a few of them, expect students to realize that these are the least dense objects and in fact, they are the objects that float. The points for all the other objects, the ones that sink, lie below the line. In other words, they are denser than water. Make sure students understand that, ordinarily, anything less dense than water floats, and anything more dense than water sinks. If students argue that ships are made of metal but float nevertheless, ask them why they think that is so. (This topic is explored in the What Floats Your Boat? lesson.)

Vocabulary/Definitions

density: The mass per unit volume of a substance at a given pressure and temperature.

Assessment

Table Test: Provide students with a table of densities of common materials. Ask them to identify the material with the highest density, and the material with the lowest density. Ask them to give an example of a material that floats in water, and a material that sinks in water. Also, ask them what the density of water is.

Final Calculations: Provide students with a list of several objects, their masses and their volumes. Ask students to calculate the density for each object, and check that they include units in their answers.

Investigating Questions

• Why do different teams often get slightly different densities for the same objects?
• How might the ways measurements are rounded affect the densities that are calculated?
• Are there any ways that more accurate density determinations could be made?
• If an object has a density greater than 1.0, will it float or sink in water?
• If salt is added to water, will the water become more dense or less dense?

Troubleshooting Tips

If students are not rounding their measurements correctly, or if they are "over-rounding" their measurements, their results may vary widely from those of their classmates and/or the known values for some of the materials. Watch students as they make their measurements to make sure they are rounding lengths to the nearest 0.5 or 1 millimeter, masses to the nearest 0.05 or 0.1 g, and water volumes to the best accuracy available for the graduated cylinders being used. Also, some students tend to always round measurements up. For example, for an actual measurement of 25.72 grams, such a student will round to 25.8 grams, rather than the correct rounding of 25.7 grams.

Activity Extensions

Provide students with ice cubes (as large and rectangular as possible) and ask them to determine the density of ice. See the associated lesson's Extension Activities section for further information and discussion ideas.

Provide each student group with a can of Coca-Cola and a can of Diet Coca-Cola. Ask them to determine the density of each. They may be surprised to find that the diet drink is less dense than the regular drink. An alternate way to demonstrate this is by simply placing each can in an aquarium of water: the diet cola floats while the regular cola sinks. Ask students to read the list of ingredients on each can and try to determine what is responsible for the density difference. Most likely it is due to the density differences in the sweeteners used, with the synthetic sweetener aspartame being less dense than the natural sugars used in non-diet soft drinks.

Copyright

Contributors

Supporting Program

Acknowledgements

This content was developed by the MUSIC (Math Understanding through Science Integrated with Curriculum) Program in the Pratt School of Engineering at Duke University under National Science Foundation GK-12 grant no. DGE 0338262. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.

This lesson and its associated activity was originally published, in slightly modified form, by Duke University's Center for Inquiry Based Learning (CIBL). Visit http://ciblearning.org/ for information about other CIBL resources for K-12 science and math teachers.