Quick Look
Grade Level: 8 (7-9)
Time Required: 1 hour
Lesson Dependency:
Subject Areas: Measurement, Physical Science

Summary
Students use modeling clay, a material that is denser than water and thus ordinarily sinks in water, to discover the principle of buoyancy. They begin by designing and building boats out of clay that will float in water, and then refine their designs so that their boats will carry as great a load (metal washers) as possible. Building a clay boat to hold as much weight as possible is an engineering design problem. Next, they compare amount of water displaced by a lump of clay that sinks to the amount of water displaced by the same lump of clay when it is shaped so as to float. Determining the masses of the displaced water allows them to arrive at Archimedes' principle, whereby the mass of the displaced water equals the mass of the floating clay boat.Engineering Connection
Density is an important property in many materials engineering applications. Building a clay boat to hold as much weight as possible is an engineering design problem.
Learning Objectives
- Students will be able to state Archimedes' principle of buoyancy.
- Students will be able to define a buoyant object as one whose density is less than that of water.
- Students will be able to describe how water pressure acts in opposition to gravity in order to make buoyant objects float.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
-
Structures can be designed to serve particular functions by taking into account properties of different materials, and how materials can be shaped and used.
(Grades 6 - 8)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
-
Requirements are the parameters placed on the development of a product or system.
(Grades
6 -
8)
More Details
Do you agree with this alignment?
State Standards
North Carolina - Science
-
Compare the physical properties of pure substances that are independent of the amount of matter present including density, melting point, boiling point, and solubility to properties that are dependent on the amount of matter present to include volume, mass and weight.
(Grade
6)
More Details
Do you agree with this alignment?
-
Understand the structure, classifications and physical properties of matter.
(Grade
6)
More Details
Do you agree with this alignment?
Pre-Req Knowledge
Students should have completed the Floaters and Sinkers lesson and its associated activity, Determining Densities.
Introduction/Motivation
Use the first of the associated activities, Clay Boats, to get students involved and interested in the subject. This activity provides students with an opportunity to use model-building as a way to help understand the forces and phenomena at work in the world around them. Both successful and unsuccessful models allow students to make inferences, refine hypotheses, and draw conclusions about the behavior of materials and structures. All of these are important aspects of the type of inquiry we call science.
After students have completed the Clay Boats activity and discussed their observations (see Activity Investigating Questions), use the second activity, Buoyant Boats, to introduce Archimedes' principle and the physics of buoyancy.
Lesson Background and Concepts for Teachers
Information about Boat Designs
Boat Hulls -- Form and Function
With photographs from books and magazines, after students complete the Clay Boats activity, they can compare their own designs to boats commonly used for trade and recreation, both past and present. They can be guided through observations about the trade-offs between speed (how fast the boat can go with a given power source), stability (how likely the boat is to tip over under a given sideways force), draft (how deeply the boat rides in the water), and cost (how expensive a given design is to build). As students consider the different types of boats and their features, try to emphasize the relationships between the design, or form, of the boat, and its function.
The more successful of the student-designed clay boats will probably resemble a flat-bottomed bowl. This design will hold many washers -- as long as the weight is carefully distributed in the boat. This is a feature of flat-bottomed boats: they require careful balancing of the cargo and passengers, or else they become unstable and prone to tip and take on water. A distinct advantage of flat-bottomed boats is that they have a shallow draft, meaning their hulls do not extend very far down below the surface of the water compared to other hull shapes (see Figure 1). Flat-bottomed boats are thus desirable for moving around in shallow water. Their simple shape also makes them the least expensive type of boat to build. Flat hulls are typically found in small utility boats such as Jon boats, and were commonly used in the last century as barges to transport goods on the quiet waters of canals in this country and in parts of Europe.
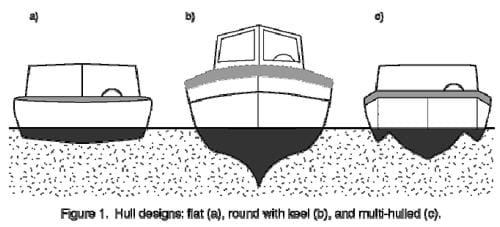
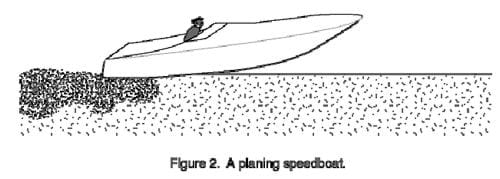
The more contemporary use for flat-bottomed boats is as high-speed runabouts for recreational purposes. In this case the flat hull is designed to rise up and ride on top of the water rather than cutting through the water, thereby encountering the reduced friction of moving through air instead of water (see Figure 2). Although it takes a lot of engine power to get the hull up, at which point the boat is said to plane, it can then travel at very high rates of speed. A disadvantage of flat hulls is that they give a rough ride if any waves are present, because the entire width of the boat's bottom is in contact with the water. (Even when planing, the back, or stern, of the boat is still in the water.)
Some students may try making boats from their clay that are shaped more like canoes, with tapered ends and rounded hulls. Tapered ends certainly let a boat move through the water more efficiently than a bowl-shape, since water can easily flow around the front (bow) of the boat if it is tapered. The rounded hull, however, presents a problem because such boats roll easily and take on water or capsize. Large sailboats, fishing trawlers, and cargo ships, which do have rounded hulls, generally also have keels. A keel is a narrow V-shaped extension of the hull along the boat's centerline that helps prevent excessive rolling (see Figure 1b). Because the keel extends down into the water, these boats cannot travel in shallow water the way boats with flat bottoms can. With their complicated hull shapes, these boats are also expensive to build.
Multi-hulled boats, such as catamarans, trimarans, pontoon boats, and some house boats, are very stable due to their wide stance in the water. Each of the hulls can be flat, but usually they are either round or V-shaped. Multi-hulled boats are usually the most expensive to build.
Superstructures and Center of Gravity
The hull shape is the main determinant of how the boat interacts with the water, but real boats carry structures and cargo above their decks, too. Structures such as cabins, masts, cranes, booms, and communications towers that are found above the deck are known collectively as the boat's superstructure. All of these affect the boat's center of gravity.
Ask students how they think a tall superstructure would affect a ship when strong winds blow from the side. Also ask how a tall superstructure would affect a ship if it rolled to one side due to large waves. If there is time and student interest, you could provide materials such as Popsicle sticks and white glue, and challenge students to make the tallest floating superstructures they can for their boats. Then you could blow on the boats from an arm's length away to test each boat's seaworthiness.
Students should be able to realize that it is necessary to keep the center of gravity as close to the midline of the ship as possible. Once the center of gravity is beyond the deck of the ship, it will tip over (just as the towers tipped over once their centers of gravity got beyond their bases). Ask students where they think heavy cargo should be placed on a ship. Point out that ships carry ballast, or extra weight (usually in the form of scrap metal), in their keels for the purpose of keeping the center of gravity low and along the midline of the ship. You can also ask students to speculate on the comparative keel depths of ships with lots of superstructure versus those with little superstructure.
Archimedes' Principle and Buoyancy
Regardless of the amount of clay students use in the second activity, Buoyant Boats, they should find that in both cases the mass of the water displaced by their clay boat is equal (or close to equal) to the mass of the boat itself. (They are asked to repeat the procedure using a different amount of clay the second time in order to generalize the phenomenon.) This is the principle of buoyancy, also known as Archimedes' Principle. When an object floats, it displaces a volume of water whose mass is equal to the object's own mass. If it can't displace this much water, the object sinks. After completing the activity, students can look back at the water levels they marked on their beakers to verify that the floating boat displaced more water than the sunken lump of clay did, a result that may have surprised them. Clay, therefore, can be a floater or a sinker, depending on its shape. It is denser than water, so ordinarily it sinks. But it can also be molded into a shape designed to displace a lot of water.
Archimedes' empirical observation is interesting, but as an explanation for how something floats it is very limited. It tells us that something has to happen, but it doesn't give us a mechanism that explains why that something happens. In order to really understand what is going on with buoyancy, it is necessary to understand the idea of water pressure.
Think of a large container of water. Water, because it is made of atoms and molecules, has mass, and the mass of the water near the surface pushes down on the water near the bottom. In other words, the water below is under pressure due to the mass of the water above. (Actually, the water at the surface is also under pressure, due to the mass of the atmosphere pressing upon it, but this pressure is much lower than the pressure at the bottom of the container.) One thing that is interesting about fluid pressure is that it is a type of force that acts in all directions at once. In contrast to gravity, which only acts downwards, water pressure pushes against any object it contacts, regardless of the orientation or location of the object within the fluid.
What this means is that if an object such as a block of wood is placed in the water, gravity acts to pull downwards on the block (tending to make it sink), but at the same time, water pressure acts upwards against the block. The water pressure counteracts the force of gravity -- in accordance with Newton's Laws of Motion -- and allows the block to float. The water pressure provides the buoyant force.
To understand this concept, it may help students to think about three blocks, each in the shape of a cube that is one foot on a side. One block is made of solid wood, and a cubic foot of wood weighs about fifty pounds. Another block is also made of wood, but it has been hollowed out in the middle, so it weighs only 10 pounds.The third block is made of solid Styrofoam™, which is very light, so it weighs only two pounds.
If you put all three blocks in a pool of water, they would all float, since they are all less dense than the water. However, the blocks would not float in quite the same way. The solid block would ride low in the water, as shown in the figure below. The Styrofoam™ would float high in the water, and the hollow wooden block would float somewhere between the two extremes.
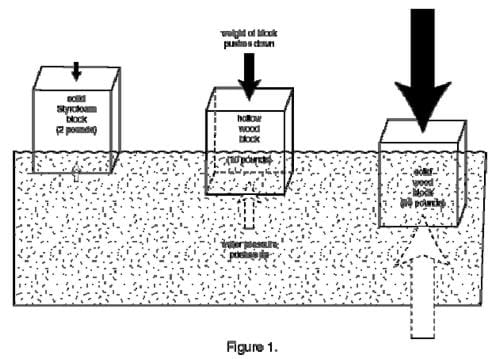
The foam block is so light that only a small amount of water pressure is needed to balance the mass of the block and let it float. The water pressure is slight up at the surface of the water, but since very little pressure is needed, the foam block does not sink very deeply into the water. The hollow wooden block, however, has to ride lower in the water in order to encounter enough water pressure to keep it afloat. The solid wood block, meanwhile, rides quite low in the water compared to the other two blocks. It has to extend even more deeply into the water than the hollow block, down to where the water pressure is high enough to counteract its greater mass.
But why does modeling clay, which is denser than water, float when it is given a bowl-like or boat-like shape? Or how do ships, for which steel is the main structural component, manage to float? The reason is that their shapes provide a large area for the water pressure to act against. The total buoyant force on an object equals the water pressure at its floating depth times the area of the object in contact with the water. This means that the more area you can give a material, the higher it can ride on the water, where the water pressure is much less. If the solid cube of wood in Figure 1 were stretched out into a plank that was eight feet long, nine inches wide, and 2 inches high, it would have the same weight and volume as the cube, but it would float nicely right at the surface of the water. This is because the plank would have six square feet of area for the water pressure to push against instead of only one square foot the block has.
Associated Activities
- Clay Boats - Using only a limited amount of modeling clay, students are challenged to design an object that not only floats, but will carry the largest load possible.
- Buoyant Boats - Students measure the amount of water displaced by a lump of modeling clay when it is shaped so as to sink in water, and then compare that amount to the amount of water the same piece of clay displaces when it is shaped so as to float in water.
Lesson Closure
Use the Activity Investigating Questions for the Buoyant Boats activity, along with the information provided in the Lesson Background & Concepts for Teachers section to discuss the results and observations of the activity. Make sure students understand that density alone isn't enough to determine whether an object will sink or float in water, but that the shape of the object can determine how much water will be displaced by the object, and thus, whether or not it will sink or float.
Vocabulary/Definitions
buoyancy : The ability to float in a liquid (or rise in a gas).
density: The mass per unit volume of a substance at a given pressure and temperature.
Assessment
- Provide students with a copy of the diagram shown in Figure 1, and ask them to write a paragraph that explains why the three objects do not float in water in quite the same ways.
- Ask students to write a paragraph that explains why a lump of clay will sink in water, but the same volume of clay, when shaped like a bowl, will float in water. Similarly, you can ask students why a bar of steel will sink in water, but ships made of steel do not. Give them the option of including diagrams with their explanations.
- Ask students to predict the weight of water that would be displaced by an empty canoe weighing 120 pounds. Assume the canoe is afloat. Also, ask if the amount of water displaced by the same canoe would increase or decrease if the canoe tipped over, filled with water, and sank.
Lesson Extension Activities
Ask students if they themselves are floaters or sinkers. Ordinarily, humans float, but barely. Our bodies contain mostly water, but we do have minerals in our bones, which are denser than water, and air in our lungs (even when we exhale fully, there is still some residual air inside), which is much less dense than water. No matter how thin we are, we all still have some amount of fat in our bodies, which is less dense than water. How easily we float depends largely on how much body fat we have. We can also float better if we fill our lungs and hold our breath.
You can also ask your students if it is easier to float in a lake (fresh water) or in the ocean (salt water). They should remember, if they have had any experience, that it is easier to float in the latter. Ask them why this is true, and give them some time to try to work out this puzzle. You may need to remind them what density really means; it is the amount of "stuff" (mass) packed into a given space, and liquids and gases have densities, too. Ocean water has salt, a type of "stuff", dissolved in the water. With more stuff in it, ocean water is denser than fresh water. Put another way, a gallon of salt water weighs more than a gallon of fresh water. Because of this weight difference, when an object floats in salt water, a smaller volume of water needs to be displaced than would be needed if the water contained no salt. Because less salt water needs to be displaced, an object floats higher in the salt water. We humans find it easier to keep our heads out of the water when we float in salt water because we don't need to displace quite as much water as we would in fresh water.
Students can design some simple experiments to compare the volumes of displaced liquid when clay boats float in fresh versus salt water. (Sea water contains about 3.5% salt, so students can make 500 mL of "artificial" sea water by combining 17.5 grams of table salt (or NaCl) with 482.5 mL of water.) You can also ask your students what would happen when a fully loaded cargo ship travels from the ocean up into a large river such as the Amazon. They can simulate this experience by making a clay boat and filling it with as many metal washers as it will hold without sinking in salt water. Then they can carefully move the boat and its load into a container of fresh water, where it will most likely sink.
If students have ever swum in a deep lake in the summer, they may have discovered that the surface water was warm, but if they dove down a few feet, the water became cooler. The colder, denser water remains at the bottom, unless something physically causes the warm and cool water to mix. (In a relatively shallow swimming pool, the action of swimmers is enough to keep the water mixed.) Students can use their clay boats to try to compare the densities of very hot and very cold water. However, the density differences are so small that students will probably not be able to measure the slight differences in the displaced volumes accurately enough to calculate any density differences. (There is only a 1.4% difference between the density of ice water at 4° C and hot tap water at 55° C.) That doesn't mean students shouldn't attempt the experiment! Their results would, in fact, lead them to conclude that no such density differences exist. They could then be asked to do some library research to find the densities of water at different temperatures, and once that was accomplished, ask them if their experimental set up would have allowed them to detect the reported differences. There is a useful lesson about the limitations of measuring methods here. You can ask your students what kinds of instruments would be needed in order to get the required accuracy.
You can also ask students to speculate about what would happen to an oil tanker that was loaded with crude oil from the very cold and very salty northern Atlantic Ocean, and then traveled to the tropical, fresh water Amazon River to deliver it. (The ship would sink lower in the water in the Amazon.) Students might be interested to know about the Plimsoll lines painted on the hulls of ships, which indicate how fully ships can be safely loaded under a variety of water and climate conditions. These are shown in Figure 2.
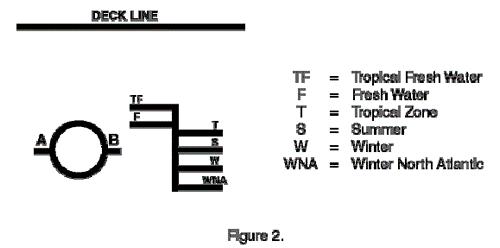
These markings came about over a hundred years ago, at a time when England was enjoying the fruits of the Industrial Revolution. Manufactured goods were being produced and exported as never before, and unfortunately, it was not uncommon for greedy ship owners to both overload and heavily insure their boats before launching them on their trade routes. As a result, a great many ships were lost; in one year alone 411 ships were wrecked along England's coast, and over 500 sailors drowned. Not surprisingly, sailors in the Merchant Navy grew reluctant to work on what they considered dangerous ships. Many were more willing to spend twelve weeks in prison for disobeying orders than they were to set sail on such vessels. At one time a prison inspector in southwest England found that nine out of twelve inmates were sailors who had been jailed for desertion.
Samuel Plimsoll, a Member of Parliament, became concerned about what he called the "coffin ships" of the times, and fought for several years for safety regulations. After several defeats of his proposals, Parliament finally passed the Merchant Shipping Act of 1876, which made load lines painted on the sides of ships mandatory. The overloading of ships was not as common in the U.S., and it wasn't until 1929 that Congress passed the Load Line Act here. Since then, the practice of applying load markings has become worldwide.
The basic load line symbol consists of a circle with a horizontal line passing through the center. The letters on either side of the circle indicate the organization that certified the load level. In the example above, the A and B stand for the American Bureau of Shipping. The placement of the line depends on a lot of factors, including various aspects of the hull shape, the length of the boat, and the type of cargo. The additional lines to the right of the circular symbol show the limits for different water types and climates, reflecting the density differences present at the time of loading.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to Pascal's law, Archimedes' principle and Bernoulli's principle. Fundamental definitions, equations, practice problems and engineering applications are supplied.

Students are challenged with determining whether the water level in a pond rises, drops or remains the same after a large rock is thrown overboard from a floating boat in a pond.

Students explore material properties in hands-on and visually evident ways via the Archimedes' principle. First, they design and conduct an experiment to calculate densities of various materials and present their findings to the class. Using this equation, they calculate the numerical solution for a...

Students learn that buoyancy is responsible for making boats, hot air balloons and weather balloons float. They calculate whether or not a boat or balloon will float, and calculate the volume needed to make a balloon or boat of a certain mass float.
References
Boat Safe. (Boat course.) Accessed June 17, 2004. http://www.boatsafe.com/nauticalknowhow
Copyright
© 2013 by Regents of the University of Colorado; original © 2004 Duke UniversityContributors
Mary R. Hebrank, project writer and consultantSupporting Program
Engineering K-PhD Program, Pratt School of Engineering, Duke UniversityAcknowledgements
This content was developed by the MUSIC (Math Understanding through Science Integrated with Curriculum) Program in the Pratt School of Engineering at Duke University under National Science Foundation GK-12 grant no. DGE 0338262. However, these contents do not necessarily represent the policies of the NSF, and you should not assume endorsement by the federal government.
This lesson and its associated activities were originally published, in slightly modified form, by Duke University's Center for Inquiry Based Learning (CIBL). Please visit http://ciblearning.org/ for information about CIBL and other resources for K-12 science and math teachers.
Last modified: March 31, 2021








User Comments & Tips