Lesson Estimating Buoyancy

Learning Objectives

After this lesson, students should be able to:

• Determine whether or not an object in air or water will float.
• Given an object's mass, calculate the volume it would need in order to float.

Educational Standards

Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.

All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).

In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.

Common Core State Standards - Math

International Technology and Engineering Educators Association - Technology

State Standards

Worksheets and Attachments

Pre-Req Knowledge

A basic understanding of algebraic concepts and density.

Introduction/Motivation

(Present this lesson on day 2 of the Balloons activity.)

What makes balloons float? (Listen to student ideas.) Balloons are filled with a gas—such as helium or hydrogen—that is less dense then the air around it, or simply a gas that is hotter than the air around it. If the density of the gas-filled balloon is less than the density of the air it displaces, the balloon will float. So, both balloons and boats float by displacing a more dense fluid with a less dense fluid (both gases and liquids are considered fluids).

Today we are going to see how we can calculate whether or not a boat or balloon will float. An object that floats is said to be buoyant. In this project, your team of engineers has been charged with building an aerial observation device to take measurements of your school. Understanding how to calculate buoyancy will help you in designing your balloon!

Lesson Background and Concepts for Teachers

The buoyant force is the result of an object displacing a fluid (both liquids and gases are considered fluids). If the mass of an object is less than the mass of liquid or gas that the object displaces, the object is said to be buoyant. Buoyancy is a force that is exerted on an object displacing a fluid. Displacing simply indicates that something is being moved out of the way. The amount of buoyancy an object has depends on the density of the fluid it is displacing, and the density of the object. If an object's mass is more than the fluid it displaces, it will sink. Alternatively, if an object has less mass than the fluid it displaces, it will float! To calculate the buoyancy of a solid object, one must know the mass and volume of the object, as well as the density of the fluid it is in. Density is a measure of mass per volume, so dividing an object's mass by the density of the fluid it is in tells you the volume of fluid the object must displace to float.

Example 1: A medical ship has a mass of 100,000 kg. What volume of fresh water (ρ=1000 kg/m³) will the ship displace?

Answer: Since the ship has a mass of 100,000 [kg], it must displace 100,000 [kg] of water to float. To convert this mass to a volume, divide by the density of freshwater (1000 [kg/m³]).

100,000 [kg] / 1,000 [kg/m³] =100 [m³3]. Therefore, the ship will displace 100 cubic meters of water.

The amount of water a ship displaces is very important to the ship's captain. If the ship is navigating shallow channels, the captain must know exactly how deep his or her ship is in the water in order to avoid hitting hidden obstacles.

Balloonists must also master buoyancy in order to control how their balloons fly. Most students are familiar with the principle that hot air rises, but how hot must air be to make a balloon fly? Table 1 shows the density of air at various temperatures: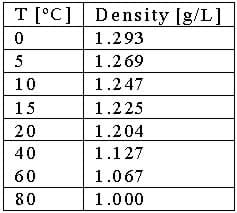

For a balloon of a given mass to fly, the balloon must be full of enough light (less dense), hot air to displace the heavier (more dense), cooler air around it. In order for an object to float, the mass of the object plus the mass of the fluid inside it must be less than the mass of the fluid it is displacing:

M +V ρ_{Inside Fluid<} V ρ_{Outside Fluid}

Where V is the volume of the displaced fluid, ρ_{Inside Fluid} is the density of the fluid inside the object and ρ_{Outside Fluid} is the density of the fluid the object displaces.

Example 2: How large must a hot air balloon be to fly? The inside temperature of the balloon is 80 ºC and the outside air temperature is 15 ºC. The balloon has a mass of 300 kg.

Answer: Rearrange the equation above to solve for V.

First, move the terms containing V to the same side by subtracting V ρ_{Inside Fluid} from both sides:

M < V ρ_{Outside Fluid} – V ρ_{Inside Fluid}

Next, factor out the V from the right side:

M < V (ρ_{Outside Fluid} - ρ_{Inside Fluid})

Finally, divide by the difference in the densities:

M / (ρ_{Outside Fluid} - ρ_{Inside Fluid}) < V

Now, insert in the known numbers to solve for V! Refer to Table 1 to find the densities, and remember to convert the mass in kg to grams:

300,000[g] / (1.225[g/L] - 1[g/L]) < V

1,333,333 [L] < V

The answer is 1,333,333 L, (or 1,333 cubic meters). That's a big balloon! What are some things we can do to make the balloon fly better? (Possible answers: Lighten the balloon, raise the inside temperature of the balloon, fly the balloon on a colder day, or increase the balloon's volume.)

Gas balloons work the same way. Different gases have different densities. Some common gasses with densities less than air include helium (ρ_Helium=0.1786 g/L), hydrogen (ρ_Hydrogen=0.0899 g/L), and neon (ρ_Neon=0.9002g/L).

Example 3: How much mass can a 10 [L] helium balloon have so that it will fly if the air in the room has a density of 1.2 [g/L]?

Answer: Find the mass of the air displaced by multiplying the density of the air in the room by the volume displaced:

10 [L] x 1.2 [g/L] =12 [g]

Find the mass of the air inside the balloon by multiplying the density of helium by the volume of helium:

10 [L] x 0.1786 [g/L] =1.8 [g]

The maximum mass the balloon can have is the difference between the two:

12 [g]-1.8 [g]=10.2 [g]

Thus, the balloon can have a mass of 10.2 grams and still fly!

Associated Activities

• Balloons - Students follow the steps of the engineering design process to create balloons for aerial surveillance. After a first attempt to create their balloons, they receive the Estimating Buoyancy lesson to learn about volume, buoyancy, and density, which helps them iterate more successful balloon designs. Their balloons carry small flip video cameras to provide aerial images, from which they draw maps and estimate areas.

Lesson Closure

Now that you know how to calculate the buoyancy of an object, you'll be responsible for using these equations to design your own balloons. If you want to use a hot air balloon, calculate how large it must be to lift your device. If you want to use helium balloons, calculate how many helium balloons you need!

Vocabulary/Definitions

buoyancy: Describes whether an object will float or sink in a given fluid.

density: The amount of mass per unit volume (mass/volume).

displace: When one thing moves something else out of the way.

Assessment

Worksheet: After going through example problems as a class, have students complete the three buoyancy problems on the attached Buoyancy Worksheet. Review their answers to assess their mastery of the concepts.

Copyright

Contributors

Supporting Program

Acknowledgements

The contents of this digital library curriculum were developed under a grant from the Fund for the Improvement of Postsecondary Education (FIPSE), U.S. Department of Education and National Science Foundation GK-12 grant no. 0338326. However, these contents do not necessarily represent the policies of the Department of Education or National Science Foundation, and you should not assume endorsement by the federal government.