Quick Look
Grade Level: 9 (9-12)
Time Required: 45 minutes
Expendable Cost/Group: US $0.00 This activity uses some non-expendable (reusable) items—a clear bucket and a toy boat; see the Materials List for details.
Group Size: 28
Activity Dependency: None
Subject Areas: Chemistry, Physical Science, Physics, Problem Solving, Reasoning and Proof
Summary
Students are presented with a challenge question that they must answer with scientific and mathematical reasoning. The challenge question is: "You have a large rock on a boat that is floating in a pond. You throw the rock overboard and it sinks to the bottom of the pond. Does the water level in the pond rise, drop or remain the same?" Students observe Archimedes' principle in action in this model recreation of the challenge question when a toy boat is placed in a container of water and a rock is placed on the floating boat. Students use terminology learned in the classroom as well as critical thinking skills to derive equations needed to answer this question.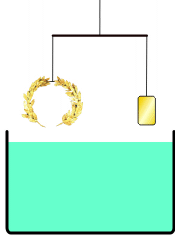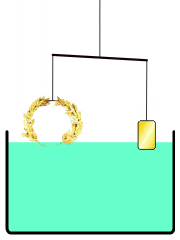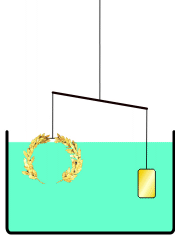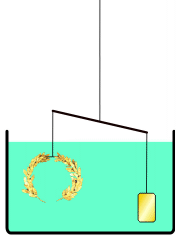
Engineering Connection
Archimedes' principle and the density-buoyancy relationship are important in science, engineering and technology applications, such as the rise of a balloon in the air and apparent loss of weight of submerged objects and various floating vessels. Naval architects and engineers design the hull shapes of ships to be buoyant by distributing their weight over a larger surface area so the weight of the water displaced is greater than the ship's weight. Engineers must also know how much water ships displace in order to help them navigate through small channels and lock-systems. Engineers also apply their understanding of buoyancy and Archimedes' principle to design stable offshore oil rigs and production platforms.
Learning Objectives
After this activity, students should be able to:
- Answer the challenge question based on an understanding of volume, mass, density and weight.
- Explain why the water level rises/falls/stays the same based on an understanding of Archimedes' principle.
Educational Standards
Each TeachEngineering lesson or activity is correlated to one or more K-12 science,
technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN),
a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics;
within type by subtype, then by grade, etc.
Each TeachEngineering lesson or activity is correlated to one or more K-12 science, technology, engineering or math (STEM) educational standards.
All 100,000+ K-12 STEM standards covered in TeachEngineering are collected, maintained and packaged by the Achievement Standards Network (ASN), a project of D2L (www.achievementstandards.org).
In the ASN, standards are hierarchically structured: first by source; e.g., by state; within source by type; e.g., science or mathematics; within type by subtype, then by grade, etc.
NGSS: Next Generation Science Standards - Science
-
Asking questions and defining problems in grades 9–12 builds from grades K–8 experiences and progresses to formulating, refining, and evaluating empirically testable questions and design problems using models and simulations.
(Grades 9 - 12)
More Details
Do you agree with this alignment?
Common Core State Standards - Math
-
Solve linear equations and inequalities in one variable, including equations with coefficients represented by letters.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
International Technology and Engineering Educators Association - Technology
-
Students will develop an understanding of the relationships among technologies and the connections between technology and other fields of study.
(Grades
K -
12)
More Details
Do you agree with this alignment?
State Standards
Texas - Science
-
know that scientific theories are based on natural and physical phenomena and are capable of being tested by multiple independent researchers. Unlike hypotheses, scientific theories are well-established and highly-reliable explanations, but may be subject to change as new areas of science and new technologies are developed;
(Grades
9 -
12)
More Details
Do you agree with this alignment?
-
express and interpret relationships symbolically in accordance with accepted theories to make predictions and solve problems mathematically, including problems requiring proportional reasoning and graphical vector addition.
(Grades
9 -
12)
More Details
Do you agree with this alignment?
Materials List
To perform this activity as a class, the following materials are needed:
- clear bucket filled with water
- toy boat (alternatives: reusable storage containers of various shapes and sizes, or make a boat using available classroom or household materials)
- large rock (or an equivalent object of varying size and weight; a good option is a metal weight used in kinetics or other physics activities)
- sticky notes and a pen, to mark water levels
- 3 or more large poster-sized sheets of paper
- pens or markers, for writing on the poster-sized papers
- Rock and Boat Worksheet, one per student
Worksheets and Attachments
Visit [www.teachengineering.org/activities/view/uoh_fluidmechanics_lesson01_activity2] to print or download.Pre-Req Knowledge
Students should have a basic understanding of Archimedes' principle and the relationship between mass, volume and density. See the Archimedes' Principle, Pascal's Law and Bernoulli's Principle associated lesson for information on these concepts.
Introduction/Motivation
Archimedes' principle and a density-buoyancy relationship are important in the engineering design of all sorts of floating vessels. For safety and efficiency, engineers analyze how floating vessels such as ships and oil platforms respond to added weight. This helps engineers design them so that they float correctly, without sinking or overturning.
Ships are designed to have different shapes and sizes depending on their purposes. For example, barges have mostly flat bottoms and are designed to carry heavy goods through rivers and canals. Tug boats, which are very powerful for their small sizes, are designed to push or pull other large vessels in crowded channels or in open bodies of water. Container ships, which are some of the largest ships in the world, are designed to carry heavy loads of containers full of products across the world. Cruise ships are large but slow and are designed as luxurious floating hotels to accommodate guests as they travel to different ports of call.
In order to prevent flooding, especially after storms, it is extremely important for engineers to know how much water ships displace in order to help them navigate through small channels and lock-systems. In today's activity, you will consider a floating boat with a rock in it, and the same floating boat with the rock fully submerged in the water. We are going to use what we have learned about Archimedes' principle to determine whether the water line will rise, fall or stay the same when the rock is taken out of the boat and placed in the water. It is your job as engineers to derive an equation to determine how the ship and water line respond to the weight and volume of the rock. You can give your results to your project engineer—ME! (the instructor) to review your engineering work and our company can later use the results to see how ships respond in different shipping channels.
Procedure
Background
Archimedes' principle states that the buoyant force of an object in water is equal to the weight of the water displaced by the object; therefore, an object sinks if the weight of the water displaced weighs less than the object, or floats if the weight of the water displaced weighs more than the object.
Archimedes' principle and the density-buoyancy relationship are important in science, engineering and technology applications, such as the rise of a balloon in the air and apparent loss of weight of submerged objects and various floating vessels. A balloon filled with helium is less dense than the surrounding air so it rises up into the atmosphere, and when an object or a human body is submerged under water, there is an apparent loss of weight equal to the weight of the water displaced by the submerged object. Naval architects and engineers design the hull shapes of ships to be buoyant by distributing their weight over a larger surface area so the weight of the water displaced is greater than the weight of the ship. It is also important to know how much water ships displace in order to help them navigate small channels and lock-systems. Engineers also apply their understanding of buoyancy and Archimedes' principle in the design of offshore oil rigs and production platforms, which are essential for the production of natural gas and petroleum from open ocean wells. It is important that oil production platforms float without sinking or overturning to ensure maximum efficiency and production of oil for consumer use.
In this activity, the boat floats because the weight of the water displaced is greater than the weight of the boat. When the rock is placed in the boat, the boat still floats because the weight of the water displaced is still greater than the weight of the boat plus the rock. When the rock is removed from the boat and placed in the water, the water line will fall because the volume of the submerged rock is less than the volume of the water displaced when the rock was in the boat.
Before the Activity
- Gather materials for the class demonstration.
- Make copies of the Rock and Boat Worksheet, one per person.
With the Students
- Write the following challenge question on the classroom board: "You have a large rock on a boat that is floating in a pond. You throw the rock overboard and it sinks to the bottom of the pond. Does the water level in the pond rise, fall or remain the same?"
- Hand out the worksheets and while students are reading the question, fill the clear bucket with water. Set the bucket on a table so the entire class can see it. Place the model boat in the water so it floats.
- Tell students that the activity today will show them how Archimedes' principle works. Choose a volunteer and ask him to come to the front of the class and place the rock in the boat. Have the volunteer write "rock in boat" on a sticky note and place the sticky note on the outside of the clear bucket so the top of the sticky note is aligned with the water level (see Figure 1-left).

Figure 1. (left) Water level when the rock is in the "boat" floating in water. (right) Water level when the rock is fully submerged in the tub of water. - Predictions: Ask students to raise their hands to answer the following questions:
- Who thinks the water line will rise when the rock is taken out of the boat and placed in the water? (Have students who raise their hands move to one side of the classroom.)
- Who thinks the water line will fall when the rock is taken out of the boat and placed in the water? (Have students who raise their hands move to a different region of the classroom.)
- Who thinks the water line will stay the same when the rock is taken out of the boat and placed in the water? (Have students who raise their hands move to a different area of the classroom.)
- Give groups each a large poster-sized sheet of paper on which to write a scientific explanation for their hypotheses: rises, falls, stays the same. Note: Depending on class size and how many students raise their hands for each of the three options, groups may be large. If a group is too large, divide it further, which results in the creation of multiple posters for some or all of the three hypotheses.
- Have the students in each group write out scientific explanations for why they chose their answers. Ask students to provide equations and diagrams if possible, and use terminology learned in class to support their answers. Allow about 20 minutes for this task. Expect that some students may change their answers upon further consideration. This is acceptable as long as they explain why they changed their answers. Have each group present its poster to the class.
- Choose a new volunteer and ask her to come to the front of the class and remove the rock from the boat and place it in the water. Have the volunteer write "rock in water" or "submerged rock" on a sticky note and place the sticky note on the outside of the clear bucket so the top of the sticky note is aligned with the new water level (see Figure 1-right). (Expect the water level to fall. Refer to the Rock and Boat Worksheet Answer Key for the mathematical theory as to why the water level falls.)
- Have students complete the worksheets and turn them in for grading. The next day, review the answers in a class discussion in order to clarify any misconceptions and reinforce answers for everyone's benefit.
Vocabulary/Definitions
buoyancy: The ability of an object to float in a liquid.
density: A measurement of the compactness of an object.
mass: A measurement of the amount of matter in an object.
mass density: Mass per unit volume of a substance.
pressure: A measurement of force per unit area.
volume: A measurement of the amount of space an object occupies.
weight: A measurement of force on an object due to gravity.
Assessment
Pre-Activity Assessment
Predictions: At the beginning of the class demonstration, ask students to hypothesize whether the water line in the pond will rise, fall or stay the same when the rock is removed from the boat and placed in the pond. Students' answers indicate their base knowledge of the activity concepts.
Activity Embedded Assessment
Brainstorming: Ask students to work together as teams to determine and write down scientific explanations using equations, diagrams and terminology learned in the classroom to support their hypotheses. This gives students the opportunity to really understand the theory behind what is happening in the activity rather than guessing the outcome. Expect some students to change their minds and others to make the connection between weight and volume to conclude the correct answer.
Post-Activity Assessment
Worksheet or Quiz: Assign students to complete the Rock and Boat Activity Worksheet in class or as homework. The worksheet encompasses definitions to help students start thinking about what these terms mean and the science behind the theories presented in class, a re-cap of the procedure, and a series of questions that guide them (even those who may be stumped!) to understanding the theory behind the activity. As a bonus question, students are asked to make engineering connections and give examples of how these principles are used in science, engineering and/or technology. Have students hand in the worksheets for grading; review their answers to gauge their depth of comprehension. The next day, review the answers as a class to clarify any misconceptions and reinforce answers for everyone's benefit. Alternatively: Modify the worksheet into a quiz by removing the objectives and procedure sections.
Troubleshooting Tips
Experiment with the activity before performing it in the classroom. If the boat capsizes when placed in the water, try a different shape and/or size boat. If using a re-usable storage container (see Figure 1), shallower containers are typically more stable than deeper containers.
If the boat sinks when the rock (or weight) is placed in the boat, try using an object of equal weight but different size (probably flatter/wider), or an object of less weight.
Activity Scaling
- For younger students, write the vocabulary words and definitions on the board at the beginning of class and clarify them during the demonstration in order to assist them in completing the worksheet.
- For more advanced students, incorporate boat dimensions or density calculations as a way to add computational questions.
Subscribe
Get the inside scoop on all things TeachEngineering such as new site features, curriculum updates, video releases, and more by signing up for our newsletter!More Curriculum Like This

Students are introduced to Pascal's law, Archimedes' principle and Bernoulli's principle. Fundamental definitions, equations, practice problems and engineering applications are supplied.

Students use modeling clay, a material that is denser than water and thus ordinarily sinks in water, to discover the principle of buoyancy. They begin by designing and building boats out of clay that will float in water, and then refine their designs so that their boats will carry as great a load (m...

Students explore material properties in hands-on and visually evident ways via the Archimedes' principle. First, they design and conduct an experiment to calculate densities of various materials and present their findings to the class. Using this equation, they calculate the numerical solution for a...

Students are introduced to the structure, function and purpose of locks and dams, which involves an introduction to Pascal's law, water pressure and gravity.
References
Hewitt, Paul. Conceptual Physics Fundamentals. San Francisco, CA: Pearson Addison Wesley, 2009.
Copyright
© 2014 by Regents of the University of Colorado; original © 2013 University of HoustonContributors
Emily Sappington, Mila TaylorSupporting Program
National Science Foundation GK-12 and Research Experience for Teachers (RET) Programs, University of HoustonAcknowledgements
This digital library content was developed by the University of Houston's College of Engineering, based upon work supported by the National Science Foundation under GK-12 grant no. DGE 0840889. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Last modified: April 11, 2019








User Comments & Tips